|
Современные методы, средства, стандарты информатики для решения прикладных задач различных классов
Метод деления отрезка пополам (метод дихотомии).
Этот метод позволяет отыскать корень уравнения с любой наперёд заданной точностью εε. искомый корень x уравнения уже отделен, т.е.указан отрезок [а, в] непрерывности функции f(x) такой, что на концах этого отрезка функция f(x) принимает различные значения:
f(a)*f(b)>0
 В начале находится середина отрезка [ a, b ]: В начале находится середина отрезка [ a, b ]:
и вычисляется значение функции в точке с, т.е. находится f(c). Если f(c)=0, то мы точно нашли корень уравнения. Если же f(c)≠0,то знак этой величины сравнивается со знаками функции y= f(x) в концах отрезка [ a, b ]. Из двух отрезков [a, с], [с, b ] для дальнейшего рассмотрения оставляется тот, в концах которого функция имеет разные знаки. С оставленным отрезком поступаем аналогичным образом. расчет прекращается, когда оставленный отрезок будет иметь длину меньше 2ε. В этом случае принимаем за приближенное значение корня середину оставленного отрезка и требуемая точность будет достигнута.
График функции.
Для выделения корней рассчитаем значения функции на заданном отрезке [0,2] с шагом 0,0001 и по полученным данным построим график функции.
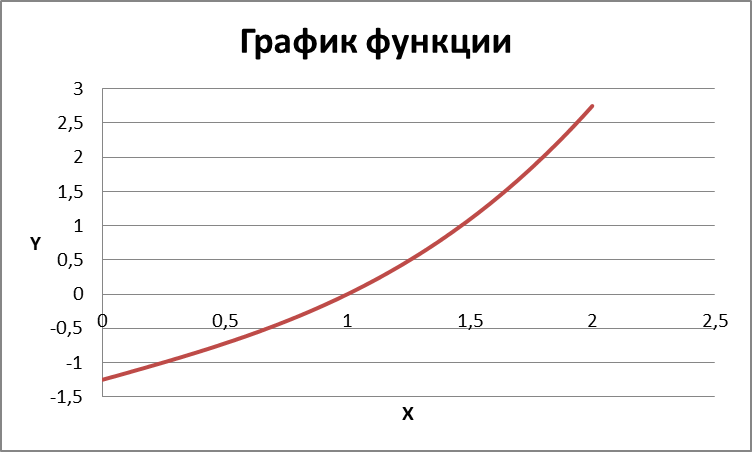
Как видно из рисунка график пересекает ось Х один раз, следовательно, на данном отрезке [0, 2] наше уравнение имеет один корень.
Метод хорд:
Этот метод заключается в том, что к графику функции проводится хорда. Находим точку пересечения с осью OX и опускаем из этой точки прямую параллельную OY. Из точки пе-ресечения прямой и графика проводим хорду и операция повторяется до тех пор, пока точка пересечения хорды с осью OX не приблизиться к корню функции до заданной погрешности.
Шаг первый:

Нас интересует точка пересечения с осью ОХ.
Сделаем допущение: х=x1
y=0
Введем обозначение
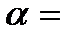 x0 x0
f( )=f(x0) )=f(x0)
Подставим в уравнение
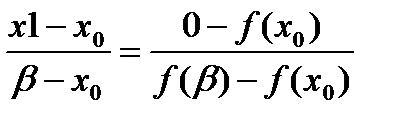
Отсюда
x1=x0- 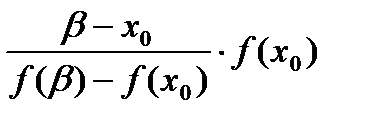
Шаг второй:
x2=x1- 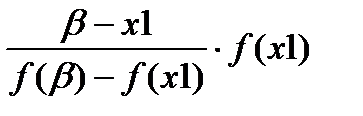
Для n-го шага:
xn=xn-1- 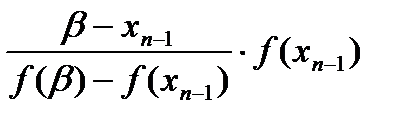
Условием нахождения корня является: 
Нелинейное уравнение и условие его решения: 0,25x3+x-1,2502=0:
График функции:

Метод Эйлера-Коши
Метод Эйлера-Коши (или усовершенствованный метод Эйлера) является методом второго порядка и заключается в следующем. Интегральная кривая на каждом шаге интегрирования заменяется прямой с тангенсом угла наклона, равным среднему арифметическому тангенсов углов наклона касательных к искомой функции в начале и в конце шага. Вычисления проводятся в следующем порядке:
1. Выбираем шаг интегрирования  . .
2. Полагаем номер шага  . .
3. Вычисляем  , находим оценку для приращения функции на этом шаге методом Эйлера , находим оценку для приращения функции на этом шаге методом Эйлера  , , 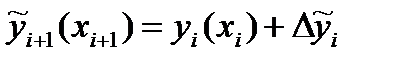 , вычисляем среднее арифметическое тангенсов углов наклона , вычисляем среднее арифметическое тангенсов углов наклона  и окончательно получаем: и окончательно получаем:
 . .
4. Если  , то увеличиваем номер шага , то увеличиваем номер шага  на единицу и повторяем п.3. В противном случае переходим к выполнению п.5. на единицу и повторяем п.3. В противном случае переходим к выполнению п.5.
5. Оформляем полученный результат.
Достоинство метода – более высокая точность вычисления по сравнению с методом Эйлера. Недостаток – больший объем вычислений правых частей.
Содержание
| РАЗДЕЛ I. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ИНФОРМАЦИОННОГО ОБЩЕСТВА
|
| | Тема 1. Предмет и основные понятия теории информационного общества
|
| | 1.1.1 Понятие и сущность информации
|
| | 1.1.2 Развитие представлений об информации
|
| | 1.1.3 Понятие и сущность информационного общества
|
| | 1.1.4 Причины и последствия информационных революций
|
| | 1.1.5 Возникновение и основные этапы развития информационного общества
|
| | Тема 2. Основные теории и концепции, относящиеся к информационному обществу
|
| | 1.2.1 Краткий анализ существующих концепций современного развития общества, воссоздающих внутреннюю логику общественного прогресса и определяющих его ближайшие перспективы: теорий постиндустриализма, информационного общества, постмодернити, постэкономической
|
| | Тема 3. Основные характеристики информационного общества. Возможности и проблемы информационного общества
|
| | 1.3.1 Основные характеристики информационного общества
|
| | 1.3.2 Роль и информационно-коммуникационных технологий
|
| | 1.3.3 Понятие "информационного общества"
|
| | 1.3.4 Противоречия и проблемы, перспективы развития информационного общества
|
| | 1.3.5 Непропорциональное использование возможностей информационно-телекоммуникационных технологий
|
| | РАЗДЕЛ II. ТЕНДЕНЦИИ РАЗВИТИЯ ИНФОРМАЦИОННОГО ОБЩЕСТВА
|
| | Тема 4. Тенденции развития информационного общества
|
| | 2.4.1 Процессы развития информационного общества
|
| | 2.4.2 Глобальный, национальный и региональный контекст формирования информационного общества
|
| | 2.4.3 Роль государства в развитии информационного общества
|
| | 2.4.4 Основные подходы к оценке готовности стран, регионов, отраслей и организаций к информационному обществу
|
| | 2.4.5 Возможности и ограничения в области регулирования развития и использования ИКТ на региональном и муниципальном уровнях
|
| | 2.4.6 Система факторов, влияющих на развитие информационного общества, их основные параметры и показатели, роль в повышении готовности страны и ее регионов к информационному развитию
|
| | Тема 5. Сетевые управленческие решения с учетом фундаментальных закономерностей преобразования информации
|
| | 2.5.1 Проблемы инвестиций в экономику информационного общества и методы оценки эффективности
|
| | 2.5.2 Методы и средства поддержки принятия управленческих решений
|
| | РАЗДЕЛ III. РАЗВИТИЕ ПОЛОЖЕНИЙ ТЕОРИИ ИНФОРМАЦИИ
|
| | Тема 6. Измерение информации в информационных системах
|
| | 3.6.1 Теоретические проблемы информатики
|
| | 3.6.2 Развитие представлений об измерении информации в фактографических, документальных и документально-фактографических информационных системах
|
| | 3.6.3 Основные теоретические положения
|
| | 3.6.4 Энтропия сложной системы
|
| | 3.6.5 Сравнительный анализ мер информации Хартли, Шеннона, Бриллюэна, Харкевича, Войшвилло
|
| | 3.6.6 Развитие представлений об оценке качества информации в информационных системах
|
| | Тема 7. Синтаксис, семантика, прагматика информационных сообщений
|
| | 3.7.1 Математические модели и основные характеристики дискретных эргодических источников сообщений
|
| | 3.7.2 Меры информации А.А. Денисова: информация восприятия (элементная база сообщения), суть (значимость) единицы воспринятой информации, содержание и смысл информации
|
| | РАЗДЕЛ IV. СОВРЕМЕННЫЕ ПОДХОДЫ К РЕШЕНИЮ ЗАДАЧ ПРИКЛАДНОГО ХАРАКТЕРА
|
| | Тема 8. Модели механизмов поиска и оценки эффективности информационных поисковых систем
|
| | 4.8.1 Язык запросов документальной автоматизированной информационно-поисковой системы (АИПС)
|
| | 4.8.2 Оценка эффективности АИПС
|
| | 4.8.3 Математические модели оценки технической эффективности
|
| | 4.8.4 Модели механизмов поиска в документальных информационных системах
|
| | Тема 9. Технологии извлечения знаний из больших баз данных
|
| | 4.9.1 Поисковые задачи и виды информационного поиска
|
| | 4.9.2 Компоненты и обобщенная схема информационного поиска
|
| | 4.9.3 Технология отбора и обработки результатов
|
| | Тема 10. Аспекты информатизации деятельности социально-экономических систем
|
| | 4.10.1 Правовые, экономические, социальные, психологические аспекты информатизации деятельности социально-экономических систем
|
| | 4.10.2 Современные методы, средства, стандарты информатики для решения прикладных задач различных классов
|
|
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




