Преобразование координат при изменении базиса
Пусть  и и 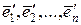 - два базиса пространства Rn. Каждый вектор - два базиса пространства Rn. Каждый вектор 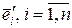 можно выразить через векторы можно выразить через векторы  : :
Выражения (5.5.1) показывают, что новые базисные векторы  получаются из старых базисных векторов получаются из старых базисных векторов 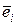 с помощью матрицы: с помощью матрицы:
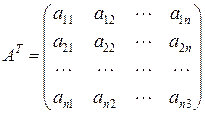 , ,
причем коэффициенты их разложений по старым базисным векторам образуют столбцы этой матрица.
Матрица А называется матрицей перехода от базиса 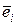 к базису к базису  . Определитель матрицы А отличен от нуля, так как в противном случае ее столбцы, а следовательно, и векторы . Определитель матрицы А отличен от нуля, так как в противном случае ее столбцы, а следовательно, и векторы  были бы линейно зависимы. были бы линейно зависимы.
Рассмотрим, как связаны между собой координаты одного и того же вектора  в старом и новом базисах. Пусть в старом и новом базисах. Пусть
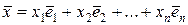
| (5.5.2)
|
и в то же время

| (5.5.3)
|
Подставим в (5.5.3) вместо  их выражения из (5.5.1): их выражения из (5.5.1):

| (5.5.4)
|
Из (5.5.2) и (5.5.4) в силу единственности разложения вектора  по базису по базису  получаем получаем
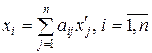 , ,
или в матричном виде
где 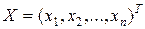 , ,  . .
Уравнение (5.5.5.) показывает связь между координатами хj и x'j вектора  в базиcах в базиcах 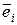 и и  , , 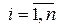 . .
Из (5.5.5.) получаем:
X'=А-1Х
Таким образом, при переходе от базиса  к базису к базису  координаты вектора координаты вектора  преобразуются с помощью матрицы А-1, являющейся обратной к транспонированной матрице, задающей преобразование базисов. преобразуются с помощью матрицы А-1, являющейся обратной к транспонированной матрице, задающей преобразование базисов.
Пример. В базисе 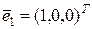 , ,  , , 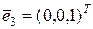 пространства R3 заданы векторы пространства R3 заданы векторы 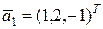 , ,  , , 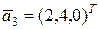 , ,  . Показать, что векторы . Показать, что векторы  образует базис. Найти координаты вектора образует базис. Найти координаты вектора  в базисе в базисе  . Выразить связь между базисами . Выразить связь между базисами  и и  . .
Решение. Векторы  образуют базис пространства R3, если они линейно независимы. Векторы образуют базис пространства R3, если они линейно независимы. Векторы  линейно независимы если векторное равенство линейно независимы если векторное равенство 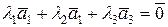 выполняется тогда и только тогда, когда выполняется тогда и только тогда, когда 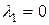 , , 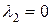 , , 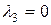 . Найдем решение векторного равенства . Найдем решение векторного равенства 
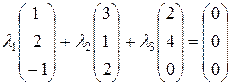
методом Жордана-Гаусса.
откуда  . .
Система векторов 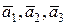 линейно независима и, следовательно, образует базис в R3. линейно независима и, следовательно, образует базис в R3.
Выразим каждый вектор 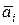 через векторы через векторы 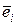 : :
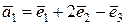
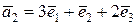

Матрица А перехода от базиса  к базису к базису 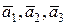 имеет вид: имеет вид:
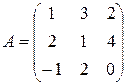 . .
Вычислив
 , ,
определим координаты 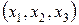 вектора вектора  в новом базисе в новом базисе
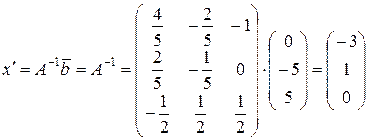 . .
Таким образом, в базисе 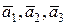 вектор вектор 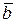 определяется координатами определяется координатами 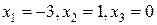 . .
Связь между базисом  и базисом и базисом 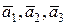 определяется из следующих соотношений: определяется из следующих соотношений:
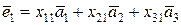 , ,
 , ,
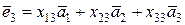 , ,
или в матричном виде:
E=XA,
где
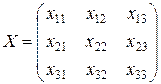 . .
Решение данного матричного уравнения имеет вид X=A-1, откуда получаем
 , ,
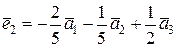 , ,
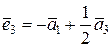 , ,
Данные соотношения выражают связь между базисами.
Евклидово пространство
n -мерное векторное пространство Еn называется евклидовым, если каждой паре векторов  и и 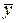 из Е поставлено в соответствие вещественное число ( из Е поставлено в соответствие вещественное число ( , , 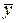 ), называемое скалярным произведением, при чем это соответствие удовлетворяет следующим аксиомам: ), называемое скалярным произведением, при чем это соответствие удовлетворяет следующим аксиомам:
I. Линейности по первому аргументу
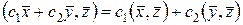 ; ;
II. Симметрии
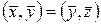 ; ;
III. Положительной определенности
 , при , при 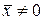
и 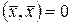 тогда и только тогда, когда тогда и только тогда, когда 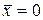 . .
Из линейности по первому аргументу и симметрии следует и линейность по второму аргументу
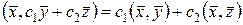
Примеры.
1. Векторами пространства En является любая упорядоченная система n действительных чисел 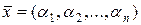 . Сложение векторов и умножение их на число определены в п.5.1, а скалярное произведение векторов . Сложение векторов и умножение их на число определены в п.5.1, а скалярное произведение векторов 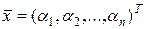 и и  определим формулой определим формулой  . .
Легко убедиться в том, что аксиомы I-III действительно выполняются.
2. Рассмотрим более общий случай. Вектор  по-прежнему определим как упорядоченную совокупность n действительных чисел. Сложение векторов и умножение их на число определим так же, как в примере 1. по-прежнему определим как упорядоченную совокупность n действительных чисел. Сложение векторов и умножение их на число определим так же, как в примере 1.
Зададимся некоторой квадратной матрицей А=(aij)n,n, Скалярное произведение векторов  и и 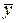 определим формулой определим формулой

| (5.6.1)
|
Рассмотрим, каким условиям должна удовлетворять матрица А, чтобы определенное данной формулой скалярное произведение удовлетворяло бы аксиомам I-Ш.
Непосредственной проверкой можно убедиться в том, что аксиома I выполняется для любой матрицы А=(aij)n,n. Для того, чтобы была выполнена аксиома II, т.е. чтобы выражение 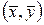 было симметричным относительно было симметричным относительно  и и 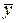 , необходимо и достаточно, чтобы , необходимо и достаточно, чтобы 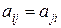 , т.е. чтобы матрица А=(aij)n,n, была симметричной. , т.е. чтобы матрица А=(aij)n,n, была симметричной.
Аксиома III требует, чтобы выражение
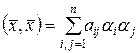
| (5.6.2)
| было неотрицательно для любых 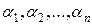 и обращалось в нуль лишь если и обращалось в нуль лишь если 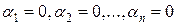 . .
Однородный многочлен (квадратичная форма), определяемый формулой (5.6.2), называется положительно определенным, если он принимает неотрицательные значения и обращается в нуль, только тогда, когда все 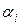 равны нулю. Следовательно, аксиома III требует, чтобы квадратичная форма (5.6.2) была положительно определенной. Таким образом, всякая матрица А=(aij)n,n задает скалярное произведение в Еn, определяемое формулой (5.6.1), если только эта матрица симметричная и соответствующая ей квадратичная форма положительно определенная. равны нулю. Следовательно, аксиома III требует, чтобы квадратичная форма (5.6.2) была положительно определенной. Таким образом, всякая матрица А=(aij)n,n задает скалярное произведение в Еn, определяемое формулой (5.6.1), если только эта матрица симметричная и соответствующая ей квадратичная форма положительно определенная.
Если а качестве матрицы А=(aij)n,n взять единичную матрицу Е, т.е. положить aii =1, а aij =0 (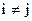 ), то скалярное произведение принимает вид ), то скалярное произведение принимает вид

и мы получаем евклидово пространство, определенное в примере 1.
3. Векторами пространства Еn будем называть непрерывные функции, заданные на интервале (а,b). Скалярное произведение таких функций определим как интеграл их произведения
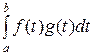 . .
Можно проверить, что при таком определении скалярного произведения аксиомы I-III выполнены.
С помощью введенного понятия скалярного произведения определим длину вектора и угол между векторами.
Определение. Нормой (длиной) 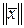 вектора вектора  в Еn называется корень квадратный из этого скалярного произведения: в Еn называется корень квадратный из этого скалярного произведения:
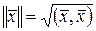 . .
Векторы  и и 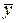 , скалярное произведение , скалярное произведение 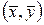 которых равно нулю, называются ортогональными. которых равно нулю, называются ортогональными.
В любом евклидовом пространстве Еn верна "теорема Пифагора": если  и и 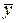 ортогональны, то ортогональны, то
 . .
Определение. Угол между ненулевыми векторами  и и 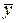 определяется равенством определяется равенством
 . .
Можно доказать, что в любом пространстве Еn справедливо неравенство Коши-Буняковского:
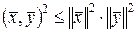 , ,
откуда следует, что

или, что то же самое,
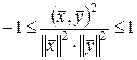
Это означает, что косинус угла между векторами из Еn по модулю, не превосходит единицы. Если  и и 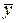 - ненулевые векторы из Еn , то ортогональность означает, что угол - ненулевые векторы из Еn , то ортогональность означает, что угол  между ними равен между ними равен 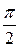 . Ненулевой вектор . Ненулевой вектор  пространства Еn, называется нормированным если его норма равна единице. Любой ненулевой вектор можно умножить на некоторое число так, что в результате получится нормированный вектор. Действительно, пусть пространства Еn, называется нормированным если его норма равна единице. Любой ненулевой вектор можно умножить на некоторое число так, что в результате получится нормированный вектор. Действительно, пусть  - ненулевой вектор. Тогда - ненулевой вектор. Тогда 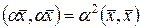 и достаточно взять и достаточно взять  таким, чтобы таким, чтобы
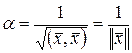
Число  называется нормирующим множителем для вектора называется нормирующим множителем для вектора  . .
Определение. Система векторов 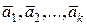 пространства Еn называется ортогональной, если векторы этой системы попарно ортогональны. пространства Еn называется ортогональной, если векторы этой системы попарно ортогональны.
Система векторов 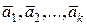 называется ортонормированной, если векторы этой системы попарно ортогональны и имеют норму, равную единице, т.е. если называется ортонормированной, если векторы этой системы попарно ортогональны и имеют норму, равную единице, т.е. если
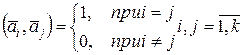 . .
Теорема. Ортогональная система ненулевых векторов пространства Еn линейно независима.
Доказательство. Пусть ненулевые векторы 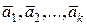 попарно ортогональны. Тогда попарно ортогональны. Тогда 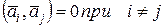 . .
Покажем, что векторное равенство
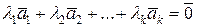
| (5.6.3)
|
выполняется тогда и только тогда, когда  . Умножим обе части равенства (5.6.3) скалярно на . Умножим обе части равенства (5.6.3) скалярно на  . Получим . Получим
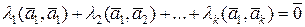
из условия ортогональности векторов имеем
 , ,  , , 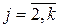 . .
Следовательно,  . Аналогично, умножая (5.6.3) на . Аналогично, умножая (5.6.3) на 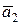 , получим что , получим что 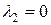 и т.д. Таким образом, мы доказали, что и т.д. Таким образом, мы доказали, что 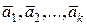 линейно независимы. линейно независимы.
Рассмотрим процесс ортогонализации векторов. Он состоит в том, что из заданных линейно независимых векторов 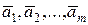 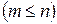 строятся m попарно ортогональных векторов строятся m попарно ортогональных векторов 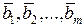 . Положим . Положим  . Вектор . Вектор 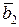 будем искать в виде будем искать в виде 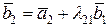 . Число . Число  следует подобрать так, чтобы векторы следует подобрать так, чтобы векторы 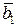 и и 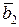 были ортогональны, т.е. были ортогональны, т.е. 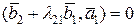 , откуда , откуда  . .
Допустим теперь, что попарно ортогональные и отличные от нуля векторы 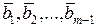 уже построены. Вектор уже построены. Вектор 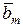 ищем в виде: ищем в виде:
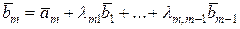 , ,
т.е. вектор 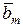 мы получаем из вектора мы получаем из вектора 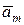 "исправлением" его с помощью линейной комбинации уже построенных векторов "исправлением" его с помощью линейной комбинации уже построенных векторов 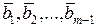 . Коэффициенты . Коэффициенты 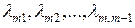 находим из условия ортогональности вектора находим из условия ортогональности вектора 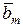 к векторам к векторам 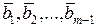 : :
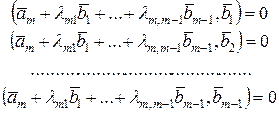
| (5.6.4)
|
Так как векторы 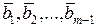 попарно ортогональны, то из равенств (5.6.4) получаем попарно ортогональны, то из равенств (5.6.4) получаем
 , ,
 , ,
……………………………
 , ,
откуда
 . .
Докажем теперь, что построенный вектор 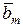 отличен от нуля. Вектор отличен от нуля. Вектор 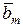 есть линейная комбинация векторов есть линейная комбинация векторов 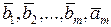 . Но вектор . Но вектор  можно заменить линейной комбинацией вектора можно заменить линейной комбинацией вектора  и векторов и векторов  и т.д. Окончательно мы получаем, что вектор и т.д. Окончательно мы получаем, что вектор 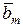 записывается в виде записывается в виде
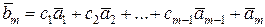
| (5.6.5)
| откуда следует, что 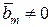 . Действительно, в противном случае левая часть равенства (5.6.5) была бы равна . Действительно, в противном случае левая часть равенства (5.6.5) была бы равна 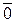 , что противоречит линейной независимости векторов , что противоречит линейной независимости векторов 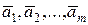 (коэффициент при (коэффициент при 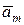 равен единице). Таким образом, доказано, что равен единице). Таким образом, доказано, что 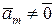 . По векторам . По векторам 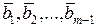 и и 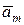 построен вектор построен вектор 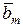 . Таким же образом, по векторам . Таким же образом, по векторам 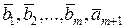 , можно построить вектор , можно построить вектор 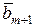 . Продолжая этот процесс, можно по заданной системе n линейно независимых векторов в Еn построить систему n ненулевых ортогональных векторов. Докажем следующую теорему. . Продолжая этот процесс, можно по заданной системе n линейно независимых векторов в Еn построить систему n ненулевых ортогональных векторов. Докажем следующую теорему.
Теорема. Во всяком евклидовом пространстве Еn существуют ортонормированные базисы.
Доказательство. По определению n -мерного векторного пространства в нем существует некоторый базис  . С помощью процесса ортогонализации из него можно построить ортогональный базис . С помощью процесса ортогонализации из него можно построить ортогональный базис  . Если теперь каждый вектор . Если теперь каждый вектор 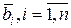 разделить на его норму, то получится ортонормированный базис, образованный векторами разделить на его норму, то получится ортонормированный базис, образованный векторами  . .
Найдем выражение скалярного произведения в координатах. Пусть 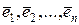 произвольный базис пространства Еn и произвольный базис пространства Еn и
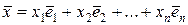 , ,
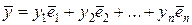 . .
Тогда
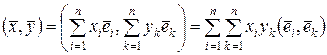 . .
Если 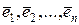 - нормированный базис, то - нормированный базис, то  , , 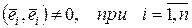 а, значит а, значит  . И обратно, если в базисе . И обратно, если в базисе 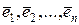 скалярное произведение векторов скалярное произведение векторов 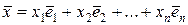 и и 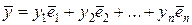 равно равно  , то этот базис ортонормированный, так как в этом случае , то этот базис ортонормированный, так как в этом случае 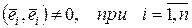 и и  . Если в некотором базисе скалярное произведение . Если в некотором базисе скалярное произведение  , то этот базис ортонормированный. , то этот базис ортонормированный.
Пусть 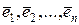 - ортонормированный базис в Еn и - ортонормированный базис в Еn и 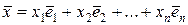 . Умножив обе части последнего равенства скалярно на . Умножив обе части последнего равенства скалярно на 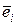 получим получим 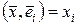 , т.е. i -я координата вектора , т.е. i -я координата вектора  в ортонормированном базисе равна скалярному произведению в ортонормированном базисе равна скалярному произведению  на единичный вектор на единичный вектор 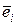 . Это скалярное произведение называется ортогональной проекцией вектора . Это скалярное произведение называется ортогональной проекцией вектора  на вектор на вектор 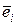 . Таким образом, координаты вектора в ортонормированном базисе – это его проекции на базисные векторы. . Таким образом, координаты вектора в ортонормированном базисе – это его проекции на базисные векторы.
Определим в пространстве Еn расстояние между векторами. Расстояние 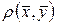 между векторами между векторами  и и 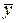 определяется как норма вектора определяется как норма вектора 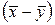 : :
 . .
Из определения расстояния следует, что
1) 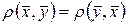 ; ;
2)  ; ;
3)  ; ;
4)  для любых для любых  из из  . .
Пример. По заданной в  системе линейно независимых векторов системе линейно независимых векторов  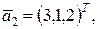  построить ортонормированный базис. построить ортонормированный базис.
Решение. Полагаем 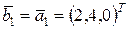 . Вектор . Вектор 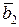 будем находить в виде: будем находить в виде: 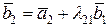 , где коэффициент , где коэффициент
 . .
Тогда 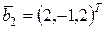 . .
Находим вектор  . .
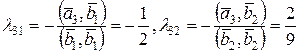
 . .
Находим нормы векторов  . .

Нормируем векторы  . Получим ортонормированный базис: . Получим ортонормированный базис:
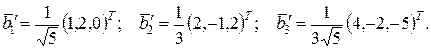
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




