Векторы, основные определения, понятия, действия над ними

Векторы, основные определения, понятия, действия над ними

Определение 1. Направленный отрезок будем называть вектором и обозначать

Определение 2. Вектор называется нулевым, если его начало и конец совпадают и обозначают

Отметим, что нулевой вектор не имеет определенного направления и имеет длину равную нулю. Это позволяет нам при записи отождествлять нулевой вектор с вещественным числом нуль.

Определение 3. Векторы называются коллинеарными, если они лежат на одной прямой, либо на параллельных прямых.

Определение 4. Два вектора называются равными, если выполнены следующие три условия: 1) длины векторов равны, 2) векторы параллельны (коллинеарны), 3) векторы направлены в одну и ту же сторону.

Определение 5. Два вектора называются противоположными, если для них выполнены первые два условия определения 4, а третье условие нарушается.

Сложение векторов

Суммой двух векторов называется вектор, идущий из начала вектора в конец вектора при условии, что вектор приложен к концу вектора (правило треугольника) и записывают (смотри рис.3.1).

Сложение векторов обладает следующими основными свойствами:

1. Коммутативность: + = +

2. Ассоциативность: для любых векторов , и выполняется равенство

3. Прибавление нулевого вектора к любому вектору не меняет последнего:

4. Сумма вектора и противоположного вектора ¹ равна нулевому вектору, т. е. + ¹ =0

Вычитание векторов

Разностью двух векторов и называется такой третий вектор , что = + и обозначает - = .

чтобы из одного вектора вычесть другой, нужно их отнести к общему началу и провести вектор из конечной точки вектора – вычитаемого в конечную точку вектора – уменьшаемого

Уравнения прямой на плоскости: с угловым коэффициентом; через две точки; в отрезках, общее уравнение

Предел числовой последовательности.

Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число a_n, то говорят, что задана числовая последовательность . То есть, числовая последовательность – это функция натурального аргумента: a_n=f(x). Числа а₁,а₂,….,а_n… называются членами последовательности, а число a_n – общим или n-ым членом данной последовательности. Можно заметить, что члены последовательности a_n с ростом n как угодно близко приближаются к 1. при этом абсолютная величина разности становится все меньше и меньше. Действительно: т.е с ростом n будет меньше сколь угодно малого положительного числа.

Число A называется пределом числовой последовательности , если для любого даже сколь угодно малого положительного числа e>0 найдется такой номер N(зависящий от e, N=N(e)), что для всех членов последовательности с номерами n>N верно неравенство: (6.2).

Предел числовой последовательности обозначается или а_n→А при n→∞. Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.

Смысл определения предела числовой последовательности состоит в том, что для достаточно больших n члены последовательности как угодно мало отличаются от числа А. Важно: номер N, не может быть указан раз и навсегда: он зависит от выбора числа Ɛ.При уменьшении Ɛ, соответствующий номер Ne, вообще говоря увеличивается.

Для геометрической интерпретации понятия предела числовой последовательности распишем неравенство: (1),

Какой бы малый отрезок (длины 2e) с центром в точке А ни взять, все точки аn, начиная с некоторой из них должны попасть внутрь этого отрезка (так, что вне его может остаться лишь конечное число этих точек).

Первый и второй замечательный предел

Теорема. (раскрывает неопределенность типа 0/0).

Второй замечательный предел - иррациональное число.

Раскрытие неопределённостей

Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:

по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.

Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.

Для раскрытия неопределённостей видов , , пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.

Для раскрытия неопределённостей типа используется следующий алгоритм:

Выявление старшей степени переменной;

Деление на эту переменную как числителя, так и знаменателя.

Для раскрытия неопределённостей типа существует следующий алгоритм:

Разложение на множители числителя и знаменателя;

Сокращение дроби.

Для раскрытия неопределённостей типа иногда удобно применить следующее преобразование:

Пусть и

Точки разрыва

Функция f(x) называется непрерывной в точке х₀, если: 1) она определена в этой точке; 2) существует ; 3) этот предел равен значению функции в точке х₀, т.е. .Если хотя бы одно из этих трёх условий не выполняется, то функция называется разрывной в точке х₀, а сама точка х₀ называется точкой разрыва функции.

Классификация точек разрыва

Различают следующие виды разрывов:

1)устранимый разрыв

2)разрыв первого рода или скачок

3)разрыв второго рода

Разрывы первого и второго рода неустранимы

Определение производной

Производной у' или f_’(x) от данной функции y= f(x) называется пре­дел отношения приращения функции к вызвавшему его приращению аргу­мента при условии, что приращение аргумента стремится к нулю:

или Производная от функции y= f(x) сама является функцией аргу­мента х.Для получения производной при определенном значении х₀ аргумента х мы придаем значению х₀ приращение Δx, что вызывает соответствующее приращение функ­ции Δy= f(x+ Δx)- f(x), затем составляем отношение приращений и вычисляем предел этого отношения, зависящего как х₀, так и от Δx, при, Δx→0 сохраняя x₀ неизменным. Следовательно, такой предел [обозначим его f’(x₀) ]

Непрерывность и дифференцируемость функции

Согласно определению, производная от данной функции y= f(x) равна пределу отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:

Но этот предел существует не для всякой функции, а если и существует, то не обязательно при всех значениях ее аргумента, для которых функция определена.

Функция, имеющая в данной точке x₀ производную, называется диф­ференцируемой в этой точке; функция, имеющая производную во всех точ­ках некоторого промежутка (a,b) называется дифференцируемой в этом про­межутке. Очевидно, что необходимым условием дифференцируемости функции в данной точке или в данном промежутке является ее непрерывность (со­ответственно в точке или в промежутке); в самом деле, предел в правой час­ти может существовать лишь тогда, когда Δy - бесконечно малая одновременно с Δx, т. е. когда функция непрерывна.

Правила дифференцирования

Операция отыскания производной от данной функции называется дифференцированием этой функции. Установим ряд правил, которые избавят нас от необходимости вычис­лять производную исходя непосредственно из ее определения.Производная от аргумента х, Полагая y=x, находим Δy =Δx. Поэтому .А так как предел постоянной равен ей самой, тo y’=1. Итак, (x)’=1Производная постоянной.Докажем, что производная постоянной равна нулю. В самом деле, если y=c, то Δy=0; поэтому при всяком Δx≠0 имеем . Но тогда (так как предел постоянной равен ей самой) Итак,(c)’=0 Производная суммы Докажем, что производная суммы дифферен­цируемых функций равна сумме их производных. Убедимся в этом для сум­мы двух функций (для большего числа слагаемых доказательство аналогич­ное).Пусть y=u+v; но тогда Δy =Δu + Δv. Деля на Δx, имеем . Отсюда, переходя к пределу при, Δx→0 находим (так как предел сум­мы равен сумме пределов): или y’=u’+v’ Производная произведения Найдем производную произведения двух дифференцируемых функций. y=u·v. Когда аргумент xполучает прираще­ние , то функции и, v и у получат соответственно приращения , Δv и Δy, причем y+Δy =(u+Δu)·(v+ Δv). Отсюда находим Δy: Δy =(u+Δu)·(v+ Δv)-u·v=v· Δu+ u· Δv+ Δu·Δv.

Дифференциал функции

Таким образом, установлены следующие предложения, характеризую­щие свойства дифференциала и связь его с приращением функции.. Дифференциал функции равен произведению ее производной на дифференциал аргумента (независимого переменного). Разность между приращением функции и Δy ее дифференциалом dy есть величина бесконечно малая более высокого порядка, чем приращение аргумента Δx, а также (при y’≠0) более высокого порядка, чем приращение функции Δy и ее дифференциал dy (в самом деле, при y’≠0 и Δx→0, Δy есть бесконечно малая того же порядка малости, что и Δx, так как dy также будет бесконечно малой того же порядка, поскольку dy=y’ ·Δy). В силу этого последнего свойства при y’≠0 приращение функции Δy и ее дифференциал dy будут при бесконечно малом равносильными бесконечно малыми:

Дифференциал функции имеет простой геометрический смысл: значение дифференциала функции, при данном значении аргумента x и данном при­ращении, Δx равно прираще­нию ординаты касательной,, проведенной в точке с абсцис­сой x графика этой функции, при переходе от точки каса­ния (с абсциссой x) к соседней точке касательной с абсциссой x+ Δx.В самом деле, соответст­вующее приращение ординаты касательной на рис. 4.5 изо­бражается катетом KN треу­гольника MKN, в котором вторым катетом служит от­резок МК= , а острый угол при вершине М равен , причем Но тогда KN = МК что и требовалось доказать.

Производные высших порядков

Если задана произвольная дифференцируемая функция , то ее производная , как известно, в свою очередь является функцией того же аргументa x. Поэтому можно ставить вопрос об отыскании производной от этой функции.

Определение производной второго порядка

Производную от производной данной функции, если она существует, называют производной второго порядка, или второй производной, от данной функции и обозначают символом . Таким образом

В связи с этим производную в дальнейшем будем называть производной первого порядка, или первой производной.

Определение производной n –го порядка. Примеры

В общем случае производной порядка n+1 от данной функции называется производной от производной порядка этой функции:

.Очевидно, что в силу принятого нами определения производных высших порядков (если они существуют у данной функции), будет справедливо такое утверждение:

Производная порядка от n-й производных высших порядков (если они существуют у данной функции), будет равна производной порядка от этой функции ( -­ целые положительные числа): .Рассмотрим несколько примеров отыскания производных высших порядков.

1. Найти производную порядка от функции .

Находим, выполняя последовательные дифференцирования:

.

2. Найти производную порядка от функций y=sin xи y=cos x.

Первую производную от, sin x равную cos x, можно записать в следующем виде: отсюда следует, что операция дифференцирования функции y=sin xпо x формально сводится к прибавлению к аргументу синуса.

В силу этого ; поэтому .

Дифференциалы высших порядков

Дифференциалом второго порядка (его обозначают символом ) от функции называют дифференциал ее дифференциала: Найдем его выражение. Имеем , причем — произвольное приращение аргумента , которое от аргумента не зависит. В виду этого при отыскании второго дифференциала функции надо рассматривать диф­ференциал независимого переменного как величину постоянную относи­тельно аргумента .

Находим

Таким образом, второй дифференциал функции равен произведению ее второй производной на квадрат дифференциала независимого переменного:d²y=y”·dx²

Правило Лопиталя.

Раскрытием неопределенности в математическом анализе называют отыскание предела , когда функция непрерывна вблизи точки , но не определена в самой этой точке, а непосредственная подстановка в формулу записи этой функции значения приводит к выражению неопре­деленного вида:

Теперь, опираясь на теорему Коши, выведем правило Бернулли — Ло­питаля для раскрытия неопределенностей, использующее производные.

Основными видами неопределенностей являются два: и .

Остальные виды неопределенностей, как увидим дальше, приводятся к основным двум видам: и .

1 случай. Неопределенность вида (при ).

Примем ; тогда функции и будут непрерыв­ными в точке .

2 случай. Неопределенность вида (при ).

Правило Бернулли — Лопиталя не применимо, если не . Но отсюда еще не следует, что не существует предел отношения самих функций, т. е. . Последний может и существовать. Но он не может только быть в этом случае найден по пра­вилу Бернулли—Лопиталя.

Теорема Лагранжа, коши

Теорема Лагранжа Если функция f(x) непрерывна на отрезке [а, b] и дифференцируема в интервале (а,b), то существует такая точка с{а,b), что

Следствие 1. Если производная функции равна нулю в каждой точке некоторого промежутка, то функция есть тождественная постоянная в этом промежутке.

Следствие 2. Если две функции имеют равные производные в некотором промежутке, то они отличаются в этом промежутке лишь постоянным слагаемым.

Корнем (или нулем) функции у = f(x) называется такое значение х = х0 ее аргумента, при котором эта функция обращается в нуль. Геометрически корень функции означает абсциссу точки, в которой график функции пересекает ось их или касается ее.

Теорема Коши: Если y = f(x) и у = у(х) - две функции, непрерывные на отрезке [а, b] и дифференцируемые в интервале (а, b) причем ф'(x) не равно 0 для любого х(а, b), то между а и b найдется такая точка с, что

Экстремум функции

Функция называется возрастающей в промежутке , если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует и большее значение функции.

Таким образом, если то Аналогично функция называется убывающей в промежутке , если для двух любых значений аргумента, принадлежащих этому промежутку, большему из них соответствует меньшее значение функции.

Если то Те значения аргумента, при которых функция достигает своих наиболь­ших или наименьших, по сравнению с соседними, значений, называются точками максимума и минимума.

Определение. Точка называ­ется точкой максимума функции , а значение называется максимумом этой функции, если существует некото­рая окрестность точки [т. е. проме­жуток ], такая, что зна­чение функции в любой точке этой ок­рестности будет меньше, чем ее значение в самой точке , т. е. меньше, чем максимум : при (5.3)

Аналогично(с заменой слова «меньше» на «больше») определяются точка минимума и минимум функции.Если — точка минимума, a мини­мум, то имеют место следующие неравенства:

при (5.4)

Максимум и минимум функции представлены на рис. 5.4 и 5.5.

Точки минимума и максимума объединяются под общим названием точек экстремума, а минимум и максимум функции объединяются общим названием экстремум функции.

Экстремумы функции , опреде­ленные выше с помощью неравенств (5.3) и (5.4), часто называются стро­гими экстремумами, в отличие от нестро­гих, где предполагаются неравенства вида и соответственно .

Таким образом, понятия максимума и минимума функции носят харак­тер локальных (местных), а не абсолютных понятий.

Таблица интегралов

Несобственные интегралы

несобственные интегралы, т. е. определенный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв.

Пусть функция непрерывна на промежутке . Если существует конечный предел , то его называют несобственным интегралом первого рода и обозначают .

Таким образом, по определению

В этом случае говорят, что несобственный интеграл сходится.

Если же указанный предел не существует или он бесконечен, то говорят, что интеграл расходится.

Аналогично определяется несобственный интеграл на промежутке :

Несобственный интеграл с двумя бесконечными пределами определяется формулой

где с — произвольное число.

В этом случае интеграл слева сходится лишь тогда, когда сходятся оба интеграла справа. Отметим, что если непрерывная функция на промежутке и интеграл сходится, то он выражает площадь бесконечно длинной криволинейной трапеции.

Интеграл с бесконечными пределами

Теорема 1. (признак сравнения). Если на промежутке непрерывные функции и удовлетворяют условию , то из сходимости интеграла следует сходимость интеграла , а из расходимости интеграла следует расходимость интеграла .

Теорема 2. Если существует предел

и ,

то интегралы

и

одновременно оба сходятся или оба расходятся (т. е. ведут себя одинаково в смысле сходимости).

Формула Грина.

Пусть в плоскости Oxy задана область R, ограниченная замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некоторой области, содержащей R, задана непрерывная векторная функция

с непрерывными частными производными первого порядка . Тогда справедлива формула Грина - кривая C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки.
Если Q=x, P=-y, то формула Грина принимает вид

где S − это площадь области R, ограниченной контуром C.
Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля. Пусть векторное поле описывается функцией

Ротором или вихрем векторного поля называется вектор, обозначаемый или и равный

Формула Грина в векторной форме записывается в виде

формула Грина вытекает из "теоремы Стокса" при переходе от трехмерного случая к случаю двух координат.

Метод Бернулли.

Решение уравнения (1) ищем в виде . Подставляем данное выражение в (1),решением которого является функция

,

где - произвольная постоянная. Перемножая , получим (3).

Интегральная формула Коши.

Основная теорема Коши позволяет вывести формулу являющуюся основной во всей теории функций комплексного переменного.

Теорема. Если функция f(z) аналитическая в односвязной области D. Тогда для любой точки z0Î D и для любого кусочно-гладкого контура l, лежащего в области D и содержащего точку z0 внутри себя, справедливо равенство: где интегрирование производится в положительном направлении замкнутого контура l.

Доказательство этой теоремы основывается на основании теоремы Коши для многосвязной области, т.к. уединяя точку z₀ обводим ее контуром К, получаем двухсвязную область, затем вводим вспомогательную функцию, где z₀ фиксированная, а z – переменная, заменяем z на t для удобства интегрирования.

Вычисление вычетов.

Правильные или устранимые особые точки. Очевидно, если z=z₀ есть правильная или устранимая особая точка функции f(z), то Res f(z₀)=0 (в разложении Лорана в этих случаях отсутствует главная часть, поэтому c-1=0).

Полюс. Пусть точка z₀ является простым полюсом функции f(z). Тогда ряд Лорана для функции f(z) в окрестности точки z₀ имеет вид:

Отсюда

Поэтому, переходя в этом равенстве к пределу при z --z₀, получаем

Res f(z0)=

(22.15.5)

Существенно особая точка. Если точка z₀ - существенно особая точка функции f(z), то для вычисления вычета функции в этой точке обычно непосредственно определяют коэффициент c-1 в разложении функции в ряд Лорана.

Векторы, основные определения, понятия, действия над ними

Определение 1. Направленный отрезок будем называть вектором и обозначать

Определение 2. Вектор называется нулевым, если его начало и конец совпадают и обозначают

Отметим, что нулевой вектор не имеет определенного направления и имеет длину равную нулю. Это позволяет нам при записи отождествлять нулевой вектор с вещественным числом нуль.

Определение 3. Векторы называются коллинеарными, если они лежат на одной прямой, либо на параллельных прямых.

Определение 4. Два вектора называются равными, если выполнены следующие три условия: 1) длины векторов равны, 2) векторы параллельны (коллинеарны), 3) векторы направлены в одну и ту же сторону.

Определение 5. Два вектора называются противоположными, если для них выполнены первые два условия определения 4, а третье условие нарушается.

Сложение векторов

Суммой двух векторов называется вектор, идущий из начала вектора в конец вектора при условии, что вектор приложен к концу вектора (правило треугольника) и записывают (смотри рис.3.1).

Сложение векторов обладает следующими основными свойствами:

1. Коммутативность: + = +

2. Ассоциативность: для любых векторов , и выполняется равенство

3. Прибавление нулевого вектора к любому вектору не меняет последнего:

4. Сумма вектора и противоположного вектора ¹ равна нулевому вектору, т. е. + ¹ =0

Вычитание векторов

Разностью двух векторов и называется такой третий вектор , что = + и обозначает - = .

чтобы из одного вектора вычесть другой, нужно их отнести к общему началу и провести вектор из конечной точки вектора – вычитаемого в конечную точку вектора – уменьшаемого

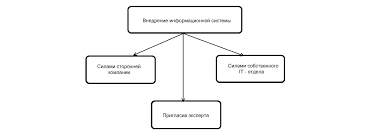Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...

ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры...

ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования...

Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор...

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: