|
|
Тема 1.ЭЛЕМЕНТЫ КОМБИНАТОРИКИСтр 1 из 7Следующая ⇒ Тема 1.ЭЛЕМЕНТЫ КОМБИНАТОРИКИ Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики. Комбинаторика происходит от латинского слова ”combinatio” соединение. Группы, составленные из каких-либо предметов, (безразлично каких, например, букв, цветных шаров, кубиков, чисел и т.п.), называются соединениями (комбинациями). Предметы, из которых состоят соединения, называются элементами. Различают три типа соединений: перестановки, размещения и сочетания.
Размещения Размещениями из n элементов по m в каждом называются такие соединения, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения. Число размещений из n элементов по m в каждом обычно обозначается символом
Понятие факториала Произведение n натуральных чисел от 1 до n обозначается сокращенно n!, то есть Например, Считается, что 0! = 1. Используя понятие факториала, формулу (1.1) можно представить так:
где Очевидно, что
Размещения с повторениями
Размещение с повторениями из n элементов по m(m × n) элементов может содержать любой элемент сколько угодно раз от 1 до m включительно, или не содержать его совсем, то есть каждое размещение с повторениями из n элементов по m элементов может состоять не только из различных элементов, но из m каких угодно и как угодно повторяющихся элементов. Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями. Число размещений с повторениями из n элементов по m элементов будем обозначать символом Можно доказать, что оно равно nm.
Сочетания Сочетаниями из n элементов по m в каждом называются такие соединения, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга по крайней мере одним элементом. Число сочетаний из n элементов по m в каждом обозначается символом
или
Сочетания с повторениями Сочетание с повторениями из n элементов по m(m Î n) элементов может содержать любой элемент сколько угодно раз от 1 до m включительно, или не содержать его совсем, то есть каждое сочетание из n элементов по m элементов может состоять не только из m различных элементов, но из m каких угодно и как угодно повторяющихся элементов. Следует отметить, что если, например, два соединения по m элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными сочетаниями. Число сочетаний с повторениями из n элементов по m будем обозначать символом
Замечание: m может быть и больше n. Перестановки Перестановками из n элементов называются такие соединения, каждое из которых содержит все n элементов, и которые отличаются друг от друга лишь порядком расположения элементов. Число перестановок их n элементов обозначается символом Рn, это то же самое, что число размещений из n элементов по n в каждом, поэтому
Перестановки с повторениями
Число перестановок с повторениями выражается при помощи формулы:
где
Правила комбинаторики
А В
|
Рис.2.2
Пересечение А и В (обозначается как A  B) есть набор, содержащий все элементы, которые являются членами и А и В.
B) есть набор, содержащий все элементы, которые являются членами и А и В.
Объединение А и В (обозначается A  B) есть набор, содержащий все элементы, которые являются членами или А, или В, или А и В вместе.(рис. 2.2)
B) есть набор, содержащий все элементы, которые являются членами или А, или В, или А и В вместе.(рис. 2.2)
БАЙЕСА
Часто мы начинаем анализ вероятностей имея предварительные, априорные значения вероятностей интересующих нас событий. Затем из источников информации, таких как выборка, отчет, опыт и т.д. мы получаем дополнительную информацию об интересующем нас событии. Имея эту новую информацию, мы можем уточнить, пересчитать значения априорных вероятностей. Новые значения вероятностей для тех же интересующих нас событий будут уже апостериорными ( послеопытными) вероятностями. Теорема Байеса дает нам правило для вычисления таких вероятностей.
Последовательность процесса переоценки вероятностей можно схематично изобразить так:





 Априорные Новая информация из Байесовский Апостериорные
Априорные Новая информация из Байесовский Апостериорные
вероятности каких-либо источников анализ вероятности
Пусть событие А может осуществиться лишь вместе с одним из событий Н1, Н2, Н3,..., Нn, образующих полную группу. Пусть известны вероятности P(H1), P(H2),…P(Hi),…P(Hn). Так как события Hi образуют полную группу, то  . Так же известны и условные вероятности события А: P(A/H1), P(A/H2), …P(A/Hi)…, P(A/Hn), i=1, 2, …, n. Так как заранее неизвестно с каким из событий Hi произойдет событие А, то события Hi называют гипотезами.
. Так же известны и условные вероятности события А: P(A/H1), P(A/H2), …P(A/Hi)…, P(A/Hn), i=1, 2, …, n. Так как заранее неизвестно с каким из событий Hi произойдет событие А, то события Hi называют гипотезами.
Необходимо определить вероятность события А и переоценить вероятности событий Hi с учетом полной информации о событии А.
Вероятность события А определяется как:
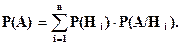 (3.1)
(3.1)
Эта вероятность называется полной вероятностью.
Если событие А может наступить только вместе с одним из событий Н1, Н2, Н3,..., Нn, образующих полную группу несовместных событий и называемых гипотезами, то вероятность события А равна сумме произведений вероятностей каждого из событий Н1, Н2,..., Нn на соответствующую условную вероятность события А.
Условные вероятности гипотез вычисляются по формуле:

или (3.2)

Это - формулы Байеса, (по имени английского математика Т.Байеса, опубликовавшего их в 1764 году) выражение в знаменателе - формула полной вероятности.
Дискретной случайной величиной называется такая переменная величина, которая может принимать конечную или бесконечную совокупность значений, причем принятие ею каждого из значений есть случайное событие с определенной вероятностью.
Соотношение, устанавливающее связь между отдельными возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения дискретной случайной величины.  Если обозначить возможные числовые значения случайной величины Х через х
Если обозначить возможные числовые значения случайной величины Х через х  , х
, х  ,...
,...  ..., а через
..., а через  вероятность появления значения
вероятность появления значения  , то дискретная случайная величина полностью определяется следующей таблицей 4.1:
, то дискретная случайная величина полностью определяется следующей таблицей 4.1:
Таблица 4.1

| 
| 
| ... | 
|

| p1 | 
| ... | 
|
где значения х  , х
, х  ,...,
,...,  ,записываются, как правило, в порядке возрастания. Таблица называется законом или рядом распределения дискретной случайной величины Х. Поскольку в верхней строчке ряда распределения записаны все значения случайной величины Х, то нижняя строчка обладает тем свойством, что
,записываются, как правило, в порядке возрастания. Таблица называется законом или рядом распределения дискретной случайной величины Х. Поскольку в верхней строчке ряда распределения записаны все значения случайной величины Х, то нижняя строчка обладает тем свойством, что
 (4.1)
(4.1)
Графическое изображение ряда распределения называется многоугольником распределения (полигоном распределения) (рис. 4.1):
 |





 |









Рис.4.1.
Для этого по оси абсцисс откладывают значения случайной величины, по оси ординат - вероятности значений. Полученные точки соединяют отрезками прямой. Построенная фигура и называется многоугольником распределения вероятностей.
Дискретная случайная величина может быть задана функцией распределения.
Функцией распределения случайной величины Х называется функция F (x), выражающая вероятность того, что Х примет значение, меньшее чем х:
 (4.2)
(4.2)
- здесь для каждого значения х суммируются вероятности тех значений  , которые лежат левее точки х.
, которые лежат левее точки х.
Функция F (x) есть неубывающая функция; 

Для дискретных случайных величин функция распределения F(x) есть разрывная ступенчатая функция, непрерывная слева (рис. 4.2):
F(x)
 | |||
 | |||
p3

 p2
p2

 p1
p1
 x1 x2 0 х3 x j
x1 x2 0 х3 x j
Рис.4.2.
Вероятность попадания случайной величины Х в промежуток от  до
до  (включая
(включая 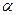 ) выражается формулой:
) выражается формулой:
 (4.3)
(4.3)
Числовые характеристики.
Математическим ожиданием дискретной случайной величины называется:

 (4.4)
(4.4)
В случае бесконечного множества значений  в правой части (4.4) находится ряд, и мы будем рассматривать только те значения Х, для которых этот ряд абсолютно сходится.
в правой части (4.4) находится ряд, и мы будем рассматривать только те значения Х, для которых этот ряд абсолютно сходится.
М(Х) представляет собой среднее ожидаемое значение случайной величины. Оно обладает следующими свойствами:
1) М(С)=С, где С=const
2) M (CX)=CM (X) (4.5)
3) M (X+Y)=M(X)+M(Y), для любых Х и Y. 
4) M (XY)=M (X)M(Y), если Х и Y независимы.
Для оценки степени рассеяния значений случайной величины около ее среднего значения M(X)= а вводятся понятия дисперсии D(X) и среднего квадратического (стандартного) отклонения  . Дисперсией называется математическое ожидание квадрата разности (X-
. Дисперсией называется математическое ожидание квадрата разности (X-  ), т.е.:
), т.е.:
D(X)=M(X-  )2=
)2=  pi,
pi,
 где
где  =М(X);
=М(X);  определяется как квадратный корень из дисперсии, т.е.
определяется как квадратный корень из дисперсии, т.е.  .
.
Для вычисления дисперсии пользуются формулой:
 (4.6)
(4.6)
Свойства дисперсии и среднего квадратического отклонения:
1) D(C)=0, где С=сonst
2) D(CX)=C2D(X),  (CX)= çCç
(CX)= çCç  (X) (4.7)
(X) (4.7)
3) D(X+Y) =D(X)+D(Y), 
если Х и У независимы.
Размерность величин  и
и  совпадает с размерностью самой случайной величины Х, а размерность D(X) равна квадрату размерности случайной величины Х.
совпадает с размерностью самой случайной величины Х, а размерность D(X) равна квадрату размерности случайной величины Х.
4.3. Математические операции над случайными величинами.
Пусть случайная величина Х принимает значения  с вероятностями
с вероятностями  а случайная величина Y- значения
а случайная величина Y- значения  с вероятностями
с вероятностями  Произведение КX случайной величины Х на постоянную величину К - это новая случайная величина, которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные произведениям на К значений случайной величины Х. Следовательно, ее закон распределения имеет вид таблица 4.2:
Произведение КX случайной величины Х на постоянную величину К - это новая случайная величина, которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные произведениям на К значений случайной величины Х. Следовательно, ее закон распределения имеет вид таблица 4.2:
Таблица 4.2

| 
| 
| ... | 
|

| 
| 
| ... | 
|
Квадрат случайной величины Х, т.е.  , - это новая случайная величина,которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные квадратам ее значений.
, - это новая случайная величина,которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные квадратам ее значений.
Сумма случайных величин Х и У - это новая случайная величина, которая принимает все значения вида  с вероятностями
с вероятностями  , выражающими вероятность того, что случайная величина Х примет значение
, выражающими вероятность того, что случайная величина Х примет значение  а У - значение
а У - значение  , то есть
, то есть
 (4.8)
(4.8)
Если случайные величины Х и У независимы, то:
 (4.9)
(4.9)
Аналогично определяются разность и произведение случайных величин Х и У.
Разность случайных величин Х и У - это новая случайная величина, которая принимает все значения вида  , а произведение - все значения вида
, а произведение - все значения вида  с вероятностями, определяемыми по формуле (4.8), а если случайные величины Х и У независимы, то по формуле (4.9).
с вероятностями, определяемыми по формуле (4.8), а если случайные величины Х и У независимы, то по формуле (4.9).
4.4. Распределения Бернулли и Пуассона.
Рассмотрим последовательность n идентичных повторных испытаний, удовлетворяющих следующим условиям:
1. Каждое испытание имеет два исхода, называемые успех и неуспех.
Эти два исхода - взаимно несовместные и противоположные события.
2. Вероятность успеха, обозначаемая p, остается постоянной от испытания к испытанию. Вероятность неуспеха обозначается q.
3. Все n испытаний - независимы. Это значит, что вероятность наступления события в любом из n повторных испытаний не зависит от результатов других испытаний.
Вероятность того, что в n независимых повторных испытаниях, в каждом из которых вероятность появления события равна  , событие наступит ровно m раз (в любой последовательности), равна
, событие наступит ровно m раз (в любой последовательности), равна
 (4.10)
(4.10)
где q=1-р.
Выражение (4.10) называется формулой Бернулли.
Вероятности того, что событие наступит:
а) менее m раз,
б) более m раз,
в) не менее m раз,
г) не более m раз - находятся соответственно по формулам:

Биномиальным называют закон распределения дискретной случайной величины Х - числа появлений события в n независимых испытаниях, в каждом из которых вероятность наступления события равна р; вероятности возможных значений Х = 0,1,2,..., m,...,n вычисляются по формуле Бернулли (таблица 4.3).
Таблица 4.3
| Число успехов Х=m | ... | m | ... | n | |||
Вероятность Р   
|

|

|

| ... |

| ... |

|
Так как правая часть формулы (4.10) представляет общий член биноминального разложения  , то этот закон распределения называют биномиальным. Для случайной величины Х, распределенной по биноминальному закону, имеем:
, то этот закон распределения называют биномиальным. Для случайной величины Х, распределенной по биноминальному закону, имеем:
M(X)=nр (4.11)
D(X)=nрq (4.12)
Если число испытаний велико, а вероятность появления события р в каждом испытании очень мала, то вместо формулы (4.10) пользуются приближенной формулой:
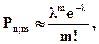 (4.13)
(4.13)
где m - число появлений события в n независимых испытаниях,  (среднее число появлений события в n испытаниях).
(среднее число появлений события в n испытаниях).
Выражение (4.13) называется формулой Пуассона. Придавая m целые неотрицательные значения m=0,1,2,...,n, можно записать ряд распределения вероятностей, вычисленных по формуле (4.13), который называется законом распределения Пуассона (таблица 4.4):
Таблица 4.4
| M | ... | m | ... | n | |||
| Pn;m | 
| 
| 
| ... | 
| ... | 
|
Распределение Пуассона часто используется, когда мы имеем дело с числом событий, появляющихся в промежутке времени или пространства. Например, число машин, прибывших на автомойку в течении часа, число дефектов на новом отрезке шоссе длиной в 10 километров, число мест утечки воды на 100 километров водопровода, число остановок станков в неделю, число дорожных происшествий.
Если распределение Пуассона применяется вместо биномиального распределения, то n должно иметь порядок не менее нескольких десятков, лучше нескольких сотен, а nр< 10.
Математическое ожидание к дисперсии случайной величины, распределенной по закону Пуассона, совпадают и равны параметру  , которая определяет этот закон, т.е.
, которая определяет этот закон, т.е.
M(X)=D(X)=n×p=  . (4.14)
. (4.14)
Нормальное распределение
Если плотность распределения (дифференциальная функция) случайной переменной определяется выражением:
 (5.10)
(5.10)
то говорят, что Х имеет нормальное распределение с параметрами а и  . Вероятностный смысл параметров:
. Вероятностный смысл параметров:  =М(X), а
=М(X), а  . Обозначение:
. Обозначение:
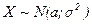
Для расчета вероятности попадания нормально распределенной случайной величины Х в промежуток от  до
до 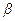 используется формула:
используется формула:
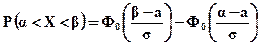 (5.11)
(5.11)
 (интеграл Лапласа)
(интеграл Лапласа)
Формула (5.11) иногда в литературе называется интегральной теоремой Лапласа.
Функция  обладает свойствами:
обладает свойствами:

3 ) 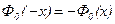 (см. таблицу приложения 2).
(см. таблицу приложения 2).
Функция  табулирована. В частности для симметричного относительно а промежутка
табулирована. В частности для симметричного относительно а промежутка 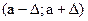 имеем:
имеем:
 (5.12)
(5.12)
Формула (5.12) применима и к частоте m, поскольку ее закон распределения при достаточно большом числе испытаний практически совпадает с нормальным. Применительно к случайной величине m, с учетом ее числовых характеристик
M(m) = np и  (5.13)
(5.13)
формула (5.12) примет вид:
 (5.14)
(5.14)
Формула (5.12) может быть применена и к относительной частоте  с числовыми характеристиками
с числовыми характеристиками  и
и 

 (5.15)
(5.15)
 (5.16)
(5.16)
С вероятностью, очень близкой к единице (равной  нормально распределенная случайная величина Х удовлетворяет неравенству:
нормально распределенная случайная величина Х удовлетворяет неравенству:
 (5.17)
(5.17)
В этом состоит правило трех сигм: если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает  .
.
Локальная теорема Муавра-Лапласа. При р  и p
и p 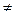 1 и достаточно большом n биноминальное распределение близко к нормальному закону (причем их математические ожидания и дисперсии совпадают), т.е. имеет место равенство:
1 и достаточно большом n биноминальное распределение близко к нормальному закону (причем их математические ожидания и дисперсии совпадают), т.е. имеет место равенство:
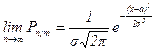 , где
, где  , a =nр
, a =nр
Тогда:
 (5.18)
(5.18)
для достаточно больших n (здесь  (х) - плотность вероятностей стандартной нормальной случайной величины
(х) - плотность вероятностей стандартной нормальной случайной величины 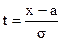 и
и  ).
).
Статистическое оценивание
Пусть из генеральной совокупности извлекается выборка объема n, причем значение признака х1 наблюдается m1 раз, х2 m2 раз,..., хk наблюдается mk раз,  - объем выборки.
- объем выборки.
Мы можем сопоставить каждому значению xi относительную частоту mi/n.
Статистическим распределением выборки называют перечень возможных значений признака xi и соответствующих ему частот или относительных частот (частостей) mi (wi).
Числовые характеристики генеральной совокупности, как правило неизвестные, (средняя, дисперсия и др.) называют параметрами генеральной совокупности (обозначают, например,  или
или  ,
,  ). Доля единиц, обладающих тем или иным признаком в генеральной совокупности, называется генеральной долей и обозначается р.
). Доля единиц, обладающих тем или иным признаком в генеральной совокупности, называется генеральной долей и обозначается р.
По данным выборки рассчитывают числовые характеристики, которые называют статистиками (обозначают  , или
, или  ,
,  , выборочная доля обозначается w). Статистики, получаемые по различным выборкам, как правило, отличаются друг от друга. Поэтому статистика, полученная из выборки, является только оценкой неизвестного параметра генеральной совокупности. Оценка параметра - определенная числовая характеристика, полученная из выборки. Когда оценка определяется одним числом, ее называют точечной оценкой.
, выборочная доля обозначается w). Статистики, получаемые по различным выборкам, как правило, отличаются друг от друга. Поэтому статистика, полученная из выборки, является только оценкой неизвестного параметра генеральной совокупности. Оценка параметра - определенная числовая характеристика, полученная из выборки. Когда оценка определяется одним числом, ее называют точечной оценкой.
В качестве точечных оценок параметров генеральной совокупности используются соответствующие выборочные характеристики. Теоретическое обоснование возможности использования этих выборочных оценок для суждений о характеристиках и свойствах генеральной совокупности дают закон больших чисел и центральная предельная теорема Ляпунова.
Выборочная средняя является точечной оценкой генеральной средней, т.е.  ≈
≈ 
Генеральная дисперсия имеет 2 точечные оценки: -  выборочная дисперсия;
выборочная дисперсия;  - исправленная выборочная дисперсия[3]. -
- исправленная выборочная дисперсия[3]. -  исчисляется при
исчисляется при  , а
, а  - при
- при  . Причем в математической статистике доказывается, что
. Причем в математической статистике доказывается, что
 или
или  (7.1)
(7.1)
При больших объемах выборки  и
и  практически совпадают.
практически совпадают.
Генеральное среднее квадратическое отклонение  так же имеет 2 точечные оценки:
так же имеет 2 точечные оценки:  - выборочное среднее квадратическое отклонение и
- выборочное среднее квадратическое отклонение и  - исправленное выборочное среднее квадратическое отклонение.
- исправленное выборочное среднее квадратическое отклонение.  используется для оценивания
используется для оценивания 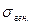 при
при  , а
, а  для оценивания
для оценивания 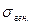 , при
, при  ;при этом
;при этом  , а
, а 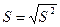 .
.
Ошибки выборки
Поскольку выборочная совокупность представляет собой лишь часть генеральной совокупности, то вполне естественно, что выборочные характеристики не будут точно совпадать с соответствующими генеральными. Ошибка репрезентативности может быть представлена как разность между генеральными и выборочными характеристиками изучаемой совокупности:  , либо
, либо  .
.
Применительно к выборочному методу из теоремы Чебышева следует, что с вероятностью сколь угодно близкой к единице можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности разность между выборочной средней и генеральной средней будет сколь угодно мала.
 (7.2)
(7.2)
где  - средняя по совокупности выбранных единиц,
- средняя по совокупности выбранных единиц,
 - средняя по генеральной совокупности,
- средняя по генеральной совокупности,
 - среднее квадратическое отклонение в генеральной совокупности.
- среднее квадратическое отклонение в генеральной совокупности.
Запись показывает, что о величине расхождения между параметром и статистикой  , можно судить лишь с определенной вероятностью, от которой зависит величина t.
, можно судить лишь с определенной вероятностью, от которой зависит величина t.
Формула (7.2) устанавливает связь между пределом ошибки  , гарантируемым с некоторой вероятностью Р, величиной tи средней ошибкой выборки
, гарантируемым с некоторой вероятностью Р, величиной tи средней ошибкой выборки  .
.
Cогласно центральной предельной теореме Ляпунова выборочные распределения статистик (при n ³ 30) будут иметь нормальное распределение независимо от того, какое распределение имеет генеральная совокупность. Следовательно:
 (7.3)
(7.3)
где Ф0(t) - функция Лапласа.
Значения вероятностей, соответствующие различным t, содержатся в специальных таблицах: при n ³ 30 - в таблице значений Ф0(t), а при n < 30 в таблице распределения t -Стьюдента. Неизвестное значение  при расчете ошибки выборки заменяется
при расчете ошибки выборки заменяется 
В зависимости от способа отбора средняя ошибка выборки определяется по разному:
Таблица 7.1
Интервальное оценивание
Мы уже знаем, что  . Если
. Если  представляет собой предел, которым ограничена сверху абсолютная величина
представляет собой предел, которым ограничена сверху абсолютная величина  , то
, то  . Следовательно,
. Следовательно,
 (7.4)
(7.4)
Мы получили интервальную оценку генеральной средней. Из теоремы Чебышева следует, что
 . (7.5)
. (7.5)
Интервальной оценкой называют оценку, которая определяется двумя числами - концами интервала, который с определенной вероятностью накрывает неизвестный параметр генеральной совокупности. Интервал, содержащий оцениваемый параметр генеральной совокупности, называют доверительным интервалом. Для его определения вычисляется предельная ошибка выборки  , позволяющая установить предельные границы, в которых с заданной вероятностью (надёжностью) должен находиться параметр генеральной совокупности.
, позволяющая установить предельные границы, в которых с заданной вероятностью (надёжностью) должен находиться параметр генеральной совокупности.
Предельная ошибка выборки равна t-кратному числу средних ошибок выборки. Коэффициент t позволяет установить, насколько надежно высказывание о том, что заданный интервал содержит параметр генеральной совокупности. Если мы выберем коэффициент таким, что высказывание в 95% случаев окажется правильным и только в 5% - неправильным, то мы говорим: со статистической надежностью в 95% доверительный интервал выборочной статистики содержит параметр генеральной совокупности. Статистической надежности в 95% соответствует доверительная вероятность - 0,95. В 5% случаев утверждение "параметр принадлежит доверительному интервалу" будет неверным. То есть 5% задает уровень значимости ( ) или 0,05 вероятность ошибки. Обычно в статистике уровень значимости выбирают таким, чтобы он не превысил 5% (
) или 0,05 вероятность ошибки. Обычно в статистике уровень значимости выбирают таким, чтобы он не превысил 5% ( < 0,05). Доверительная вероятность и уровень значимости дополняют друг друга до 1 (или 100%) и определяют надежность статистического высказывания.
< 0,05). Доверительная вероятность и уровень значимости дополняют друг друга до 1 (или 100%) и определяют надежность статистического высказывания.
С помощью доверительного интервала можно оценить не только генеральную среднюю, но и другие неизвестные параметры генеральной совокупности.
Для оценки математического ожидания а (генеральной средней ) [5]нормально распределенного количественного признака Х по выборочной средней  при известном среднем квадратическом отклонении s генеральной совокупности (на практике - при большом объеме выборки, т.е. при n ³ 30) и собственно-случайном повторном отборе формула (7.5.2) примет вид:
при известном среднем квадратическом отклонении s генеральной совокупности (на практике - при большом объеме выборки, т.е. при n ³ 30) и собственно-случайном повторном отборе формула (7.5.2) примет вид:
 (7.6)
(7.6)
где t определяется по таблицам функции Лапласа из соотношения
2F0(t) = g;
 - среднее квадратическое отклонение;
- среднее квадратическое отклонение;
n - объем выборки (число обследованных единиц).
D определяется по формуле:

Для оценки математического ожидания а (генеральной средней ) нормально распределенного количественного признака Х по выборочной средней 

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...

Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...

ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования...

Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все...
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: