Ну и последняя третья проблема из нашего списка когда у нас не
 а а  или не дай бог или не дай бог 
При иложении проблемы я буду неиного упрощать схему и критерии АШР буду говорить только о первом - Методе прямого отбора и о его критерии как минимуме остаточной дисперсии или максимуме точности модели- эти упрощения непринципиальны так как речь пойдет все о том же - о множкственности получаемых моделей и о необоснованности выбора структуры классическими алгоритмами.
И так принимаем в полном соответствии с критерием МНК синтезируемая модель должна стремиться к максимальной точности – мин МСЕ.
И так возращаемся к десткому вопросу при моделировании – что такое хорошо и что такое плохо. + То есть что такое хорошая модель и что такое плохая.
И вообще – мы часто подменяем суть задачи - хотим решать одну но не можем ее решить (получить качественную модель во всей области определения) - тогда решаем другую попроще, которую можем решить (точную только в известных точках) и пользуюмся ей как будто решили ту, более сложную
при нарушении условия 1. (а это также наиболее распространенный случай задач когда точек не тысячи а сотня или десяток –два -пять – особенно при структурно-пар синтезе) мы говорим о применении большой полезной группы методов под общим названием МИМ –Методы индуктивного К----- моделирования (в том числе МГУА – укр. изобретение - Ивахненко)
Метод группового учета аргументов
Понятие внешнего критерия. Критерий регулярности.
Таким образом появилась идея внешних критериев, идея подстройки структуры модели на новой, свежей информации, не использованной для оценки параметров. Эта идея позволяет разумно решить проблему множественности предлагаемых алгоритмами моделей, проблему, как найти среди этих моделей истинную или хотя бы ту которая, вела бы себя как истинная, касательно тех свойств которые нас интересуют прежде всего.
Формальное определение.
Под внешним критерием понимается мера наиболее важного для определения структуры модели свойства (точность аппроксимации или, прогноза, дискриминации или гладкости …..) вычисленная по информации, не использованной при оценке параметров модели.
Один из наиболее распространенных внешних критериев (критерий селекции структур) – это критерий регулярности 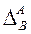 . .
Критерий регулярности.
Пусть полная выборка данных обозначена  . Поделим ее на 2 подвыборки . Поделим ее на 2 подвыборки 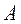 и и  такие что такие что  , ,  , ,
 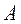 называют обучающей выборкой (learning) на которой оцениваем параметры модели. Для нее нормированная среднеквадратичная ошибка называют обучающей выборкой (learning) на которой оцениваем параметры модели. Для нее нормированная среднеквадратичная ошибка  равна равна  , где , где 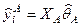
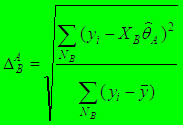
 - называют проверочной выборкой (training) на которой отбираем структуры. Нормированная среднеквадратичная ошибка - называют проверочной выборкой (training) на которой отбираем структуры. Нормированная среднеквадратичная ошибка  для той же модели равна для той же модели равна 
Что и называют критерием регулярности
В чем смысл критерия? - если модель без подстройки параметров (а только за счет структуры, ведь параметры оцениваем на А) неплохо угадывает прогноз или аппроксимацию на свежих точках (на В), то наверное и на некоторых других свежих (будущих - выборка С) точках следует ожидать неплохих результатов.
Данная идея и соответствующий подход впервые появились именно в Украине (кроме подхода кросс-валидейшн- о нем позже) – в школе ак. Ивахненко А.Г. в 1968гг. и получил название метода группового учета аргументов (МГУА).
Но идея МГУА гораздо шире критерия регулярности – это подход о необходимости выбора внешнего критерия для отбора структур.
А разнообразие внешних критериев дало возможность эффективного применения МГУА практически во всех типах задач моделирования – прогноза, аппроксимации, классификации подробно мы об этом поговорим видимо в другом курсе – технической кибернетики. Кстати именно А,Г, Ивахненко, 1959 автор этого термина.
Схема МГУА
В наиболее общем виде алгоритм МГУА нашел свое отражение в следующей обобщенной схеме:
    
                 1 2 …. K 1 2 …. K


Рис. Общая схема алгоритма МГУА
Схему проиллюстрируем для варианта МГУА на основе внешнего критерия – критерия регулярностиГ– блок: генератор частных описаний (моделей претендентов)
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|















 1 2 …. K
1 2 …. K






