|
|
Краткий курс математического анализаСтр 1 из 5Следующая ⇒ Галкин С.В.
Краткий курс математического анализа В лекционном изложении для студентов МГТУ им. Н. Э. Баумана (третий семестр)
Москва 2005.
Часть1 Кратные и криволинейные интегралы, теория поля. Лекция 1. Двойной интеграл. Вычисление двойного интеграла в декартовой системе координат.
Предположим, что D – плоская область, лежащая в некоторой плоскости и введем в этой плоскости декартову систему координат. Область D назовем правильной, если любая прямая, параллельная декартовым осям, пересекает ее не более чем в двух точках. Можно показать, что замкнутую ограниченную область с кусочно-гладкой границей можно представить в виде объединения правильных областей, не имеющих общих внутренних точек. Поэтому интеграл по области D можно вычислять как сумму интегралов (свойство 2) по правильным областям. Будем считать, что нам надо вычислить двойной интеграл по правильной области.
Подставляя
Примеры. Записать двойной интеграл по заданной области и повторные интегралы. 1.
Геометрический и физический «смысл» двойного интеграла.
К двойному интегралу В этом и состоит его геометрический смысл. Можно рассмотреть задачу о массе плоской пластины, представляющей собой плоскую область D, плотность которой равна Поэтому физический смысл двойного интеграла заключается в том, что
Пример. Вычислить объем V цилиндрического тела, ограниченного двумя параболическими цилиндрами z = 1-y2 и x = y2 и площадь его основания D, расположенного в плоскости OXY..
Приложения двойного интеграла.
С помощью двойного интеграла можно вычислить объем цилиндрического тела, площадь и массу плоской области. От этих задач мы и пришли к двойному интегралу. Но возможны и менее очевидные приложения. С помощью двойного интеграла можно вычислять площадь поверхности, определять статические моменты, моменты инерции и центр тяжести плоской области. Вычисление статических моментов, координат центра тяжести, моментов инерции.
Пусть задана плотность вещества плоской материальной области D r(x, y). Выделим элементарную ячейку с массой dm и применим к ней известные формулы для материальной точки: Статические моменты относительно осей OX, OY dmx = y dm = y r(x, y) ds, dmy = x dm = x r(x, y) ds. Моменты инерции относительно осей OX, OY dJx = y2 dm = y2 r(x, y) ds, dJy = x2 dm = x2 r(x, y) ds. Момент инерции относительно начала координат dJ0 = dJx + dJy.
Двойным интегралом по всей области D вычисляем те же характеристики для области D.
Координаты центра тяжести Пример. Вычислить координаты центра тяжести полукруга
Поэтому Пример. Вычислить момент инерции полукруга
Эта формула известна в теоретической механике.
Лекция 3 Тройной интеграл. Лекция 4. Приложения тройного интеграла.
Задача о работе силы.
1. Организуем разбиение области- дуги AB на элементы – элементарные дуги 2. Отметим на элементах разбиения «отмеченные точки» Mi и вычислим в них значения функции 3. Построим интегральную сумму 4. Переходя к пределу при условии
Теорема существования. Пусть вектор - функция
Замечание. Предел этот не зависит от - способа выбора разбиения, лишь бы выполнялось условие А - выбора «отмеченных точек» на элементах разбиения, - способа измельчения разбиения, лишь бы выполнялось условие В
Лекция 6. Формула Грина.
Теорема (формула) Грина. Пусть G – плоская односвязная область с кусочно-гладкой границей L. Пусть функции P(x, y), Q(x, y) непрерывны и имеют непрерывные частные производные по своим переменным в области G и на L. Тогда справедлива формула Грина
Доказательство. 1) Назовем плоскую область D (в плоскости OXY) правильной, если любая прямая, параллельная координатной оси (OX или OY) пересекает область не более, чем в двух точках. Можно показать, что область G можно представить как объединение конечного числа правильных областей Тогда по свойству аддитивности двойной интеграл в правой части формулы Грина равен сумме двойных интегралов по правильным областям. Криволинейный интеграл в левой части равен сумме криволинейных интегралов по границам правильных областей, так как криволинейные интегралы по общим границам любых правильных областей различны по знаку из-за различных направлений обхода границы и взаимно уничтожаются при суммировании. Поэтому доказательство может быть проведено для правильной области G. 2) Пусть G – правильная область. Так как P, Q могут быть произвольными функциями, то формула Грина сводится двум формулам
Формула Ньютона – Лейбница. Пусть выполнены условия теоремы о полном дифференциале и пусть выражение
Тогда справедлива формула Ньютона – Лейбница
Доказательство. В теореме о полном дифференциале доказано, что потенциал можно записать в виде Лекция 8 Скалярное и векторное поля. Говорят, что в области (плоской или пространственной) задано скалярное поле j (M), если в этой области задана скалярная функция j (M). Говорят, что в области (плоской или пространственной) задано векторное поле Например, масса или температура частиц в комнате – скалярные поля, скорость или силы взаимодействия частиц – векторные поля. В интегралах первого рода:двойных, криволинейных, поверхностных мы имели дело со скалярным полем – распределением масс точек кривой или поверхности в пространстве. В интегралах второго рода вычислялись характеристики векторных полей: работа векторного поля (силового поля) в криволинейном интеграле, поток векторного поля в поверхностном интеграле. Рассмотрим подробнее основные характеристики скалярных и векторных полей.
Скалярные поля.
Линии уровня плоского поля j (x, y) – кривые, на которых значения функции постоянны j (x, y) = С. Например, линии равной высоты, нанесенные на географической карты (h (x, y) = 0 – уровень моря, h = 7000м – немногие горные вершины, h = - 10000м – самые глубокие океанские впадины). Поверхности уровня пространственного поля j (x, y, z) – поверхности, на которых значения функции постоянны j (x, y, z) = С. Например, поверхности равной температуры или давления в атмосфере. Любая линия на поверхности уровня – это линия уровня. Пример. Задано поле Линии или поверхности различных уровней не пересекаются. Чем чаще (гуще) поверхности или линии уровня, тем интенсивнее изменение поля. Градиент поля – вектор Утверждение. Градиент скалярного поля ортогонален его поверхности уровня. Доказательство. Пусть точка (x, y, z) остается на поверхности уровня g(x, y, z) = 0 при вариациях переменных. Тогда равенство превращается в тождество, а тождество можно дифференцировать.
Вектор
Производная скалярного поля по направлению
Пример. Найти производную скалярного поля g(x, y, z) = x2 + y2 + z3 по направлению {1,3,2} в точке (1,0,4)
Векторное поле.
Векторная линия -линия, в каждой точке которой вектор поля направлен по касательной к ней. Уравнения векторной линии легко получить из условия коллинеарности векторов поля
Пример. Написать уравнения векторных линий векторного поля
Векторной трубкой называется поверхность, образованная векторными линиями.
Свойства дивергенции. 1) Линейность.
2)
3)
Лекция 9 Формула Стокса. Ротор векторного поля. Назовем ротором векторного поля
Свойства ротора. 1) Линейность
2)
3)
Теорема Стокса.
Пусть пространственно односвязная область V содержит кусочно-гладкую поверхность Пусть компоненты векторного поля Тогда справедлива формула Стокса
Замечание. Нормаль к поверхности
Доказательство теоремы Стокса.
представляет собой вектор Отсюда видно, что
(на поверхности = Используем формулу Грина для области D с ее границей
= В самом деле, на контуре Одна из частей формулы Стокса доказана.
Линейным интегралом векторного поля Линейный интеграл имеет смысл работы векторного поля при перемещении по дуге.
Циркуляцией векторного поля называется линейный интеграл по замкнутому контуру.
Вводя эти понятия, можно записать формулу Стокса в «полевой» форме
Мы определили ротор векторного поля в декартовой системе координат, однако ротор – это характеристика самого векторного поля Поэтому необходимо дать определение ротора, которое не зависит от выбора системы координат.
Инвариантное определение ротора. Рассмотрим произвольную точку M в области V. Проведем через нее поверхность
Здесь, как и ранее
Это и есть инвариантное определение ротора. Правая часть формулы – это поверхностная плотность циркуляции векторного поля (энергии в точке M вращения векторного поля или работы векторного поля при вращении вокруг некоторого направления, определяемого вектором Если направление Левая часть достигает максимума при коллинеарности направления и ротора векторного поля. Поэтому направление ротора векторного поля – это то направление, вокруг которого поверхностная плотность циркуляции векторного поля – наибольшая. Пример. Найти ротор линейной скорости вращения с постоянной угловой скоростью
Векторное поле линейной скорости
Ранее была сформулирована теорема о полном дифференциале для пространственной кривой. В ее доказательстве не хватало только одного пункта – перехода от пункта 3) к пункту 2). Все остальное доказывается аналогично случаю плоской кривой.
Оператор Гамильтона Оператор Гамильтона Применим оператор Гамильтона к скалярному полю Оператор Гамильтона представляет собой вектор-оператор. Его можно скалярно или векторно умножить на векторное поле
Это дифференциальные операции первого порядка над скалярным и векторным полями. От скалярного поля можно взять градиент, от векторного поля можно взять дивергенцию и ротор. Гармоническое поле. Скалярное поле
Векторное поле называется гармоническим, если оно потенциальное ( Теорема. Для того, чтобы векторное поле Необходимость. Если векторное поле Достаточность. Если векторное поле
Так как гармоническое поле потенциально и соленоидально, то его свойства – свойства соленоидального поля и свойства потенциального поля.
Свойства сходящихся рядов. 1. Члены сходящегося ряда можно умножить на одно и то же число k. Полученный ряд будет сходиться, а сумма его будет в k раз больше суммы исходного ряда.
Доказательство. Для второго ряда частичная сумма будет равна
2. Члены сходящегося ряда можно группировать. Полученный ряд будет сходиться, и сумма его не изменится.
Сгруппируем члены ряда, например, так
3. В сходящемся ряде можно отбросить конечное число первых членов
Запишем частичные суммы второго ряда Замечание. Ряд, полученный из исходного ряда отбрасыванием первых k членов, называется остатком ряда и обозначается
4. Для того чтобы ряд сходился необходимо и достаточно, чтобы сходился остаток ряда. (Докажите это самостоятельно, используя доказательство свойства 3). Поэтому сходимость ряда можно исследовать, «начиная с некоторого n».
5. Сходящиеся ряды можно складывать (или вычитать), получая сходящийся ряд с суммой, равной сумме (или разности) сумм исходных рядов.
Рассмотрим два сходящихся ряда
Примеры. 1. Ряд –5+7-8+100+1+0,5+0,25+0,125+… сходится. В самом деле, отбросив первых четыре члена ряда (свойства 3,4), получим сходящуюся бесконечно убывающую геометрическую прогрессию 2. Ряд 3. Ряд
Интегральный признак Коши.
Доказательство. Так как . Достаточность. Если интеграл сходится, то Необходимость. Если ряд Если ряд расходится, то и интеграл расходится и наоборот. Это легко доказывается от противного. Поэтому говорят, что несобственный интеграл и ряд сходятся или расходятся «одновременно», т.е. один из них сходится, то и другой сходится, если один расходится, то и другой расходится. Это понятие часто употребляют при сравнении рядов.
Пример. Применим интегральный признак к гармоническому ряду.
Пример. Рассмотрим «ряды Дирихле»
Интересно, что ряд Теперь становится яснее, где пролегает граница между сходящимися и расходящимися рядами. Заодно накоплена библиотека сходящихся и расходящихся рядов, которые можно использовать как эталонные при сравнении рядов. Сравнивать ряды можно с помощью признаков сравнения.
Признаки сравнения рядов. Второй признак сравнения. Пусть Доказательство. Раскроем определение предела.
Если ряд Если ряд Пусть ряд Пусть ряд
Пример. Ряд с   ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала... 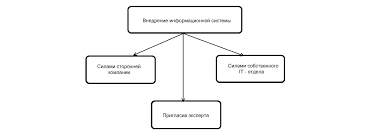 Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)... 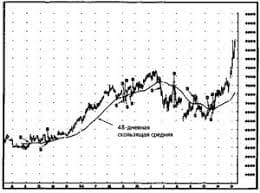 Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот... 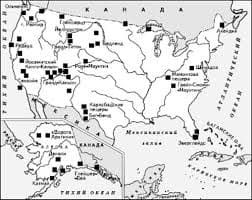 Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|