|
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ
Драчева И.А., Ершова Т.Г.
МАТЕМАТИКА
Методические указания
для самостоятельной работы и выполнения контрольной работы
для студентов заочной формы обучения
направления 39.03.02 «Социальная работа»
Керчь, 2015
УДК 51
| Авторы (составители):
| Драчева И.А., старший преподаватель кафедры математики, физики и информатики ФГБОУ ВО «КГМТУ»____________
Ершова Т.Г., преподаватель кафедры математики, физики и информатики ФГБОУ ВО «КГМТУ»____________
| |
|
| | Рецензент:
| Кузьменко С.Н., к. физ.-мат. наук, доцент кафедры математики, физики и информатики ФГБОУ ВО «КГМТУ» _______________
| | | | |
Методические указания рассмотрены и рекомендованы к утверждению на заседании кафедры математики, физики и информатики ФГБОУ ВО «КГМТУ»,
протокол № от 2015 г.
Заведующий кафедрой ___________________ Т. Н. Попова
Методические указания утверждены и рекомендованы к изданию на заседании методической комиссии технологического факультета ФГБОУ ВО «КГМТУ»,
протокол № от 2015 г.
| ©
| ФГБОУ ВО «Керченский государственный морской технологический университет», 2015 г.
|
Содержание
|
| ВВЕДЕНИЕ…………………………………………………………….
|
| | 1.
| КОНТРОЛЬНЫЕ ЗАДАНИЯ………………………………………….
|
| | 2.
| ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ………………………..
|
| | 3.
| КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ И РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ.....................................................................................................
|
| |
| 3.1 Задания типа 1-10…………………………………………….......
|
| |
| 3.2 Задания типа 11-20……………………………………………….
|
| |
| 3.3 Задания типа 21-30……………………………………………….
|
| |
| 3.4 Задания типа 31-40……………………………………………….
|
| |
| 3.5 Задания типа 41-50……………………………………………….
|
| |
| 3.6 Задания типа 51-60 ………………………………………………
|
| |
| 3.7 Задания типа 61-70……………………………………………….
|
| | 4.
| ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЧЕТУ………………………...
|
| |
| СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ…………………….
|
|
ВВЕДЕНИЕ
«Математика» является одной из базовых дисциплин математического и естественнонаучного цикла подготовки бакалавров по направлению 39.03.02 «Социальная работа». Знания, приобретенные в результате изучения математики, необходимы для успешного изучения информатики, методики и техники социологических исследований, методах исследования в социальной работе, социальной квалиметрии, социальной информатики.
В результате изучения математики формируются общекультурные и профессиональные компетенции: владение культурой мышления, способность к обобщению, анализу, восприятию информации, постановке цели и выбору путей её достижения; умение логически верно, аргументировано и ясно строить устную и письменную речь; стремление к саморазвитию, повышению своей квалификации и мастерства; использование в профессиональной деятельности методов математического анализа и моделирования, теоретического и экспериментального исследования; способность к участию в работе научных коллективов, проводящих исследования по различным направлениям обеспечения социального благополучия.
Настоящие методические указания содержат вопросы для подготовки к зачету по математике, контрольные задания и методические указания к решению задач. Методические указания включают следующие разделы математики: линейная алгебра, функция, предел функции, производная функции, интегральное исчисление, теория вероятностей и математическая статистика.
Студент заочной формы обучения при выполнении контрольных работ должен знать следующие рекомендации:
- контрольную работу необходимо выполнить в отдельной тетради, на обложке которой должны быть указаны фамилия и инициалы студента, полный шифр, дата регистрации работы в университете;
- при решении задач необходимо указать номер задачи ее содержание;
- решение задачи должно сопровождаться достаточно подробными пояснениями;
- все вычисления должны быть приведены полностью, чертежи и графики выполнены аккуратно;
- для удобства рецензирования преподавателем контрольной работы следует на каждой странице оставлять поля.
После получения отрецензированной работы студент должен исправить в ней все ошибки. Если работа не допущена к защите, то в кратчайший срок студенту необходимо после устранения замечаний преподавателя представить работу на повторное рецензирование. Ошибки следует исправлять в той же тетради. Перед экзаменом или зачетом студент должен защитить контрольную работу. При защите студент должен быть готов дать пояснения к решенным задачам или решить подобные задачи. На экзамен (или зачет) необходимо представить преподавателю все запланированные контрольные работы.
Студент выполняет тот вариант контрольной работы, который совпадает с последней цифрой его учебного шифра.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Таблица 1.
| Вариант
| Номера задач контрольных заданий
| Вариант
| Номера задач контрольных заданий
| |
| 1, 11, 21, 31, 41, 51, 61
|
| 6, 16, 26, 36, 46, 56, 66
| |
| 2, 12, 22, 32, 42, 52, 62
|
| 7, 17, 27, 37, 47, 57, 67
| |
| 3, 13, 23, 33, 43, 53, 63
|
| 8, 18, 28, 38, 48, 58, 68
| |
| 4, 14, 24, 34, 44, 54, 64
|
| 9, 19, 29, 39, 49, 59, 69
| |
| 5, 15, 25, 35, 45, 55, 65
|
| 10, 20, 30, 40, 50, 60, 70
|
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ
Задания 1-10.
Дана система линейных уравнений. Решить систему по формулам Крамера.
| 1.
| 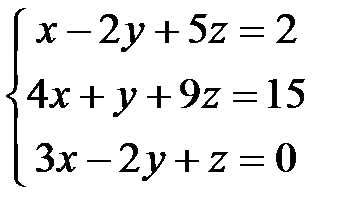
| 2.
| 
| | 3.
| 
| 4.
| 
| | 5.
| 
| 6.
| 
| | 7.
| 
| 8.
| 
| | 9.
| 
| 10.
| 
|
Задания 11-20.
Найти указанные пределы (не пользуясь правилом Лопиталя).
|
11.
| а)  б) б) 
| |
12.
| а)  б) б) 
| |
13.
| а)  б) б) 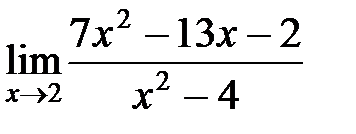
| |
14.
| а)  б) б) 
| |
15.
| а)  б) б) 
| |
16.
| а)  б) б) 
| |
17.
| а)  б) б) 
| |
18.
| а)  б) б) 
| |
19.
| а)  б) б) 
| |
20.
| а)  б) б) 
| Задания 21-30. Найти экстремумы функции, интервалы возрастания, убывания.
21. 
| 22. 
| 23. 
| 24. 
| 25. 
| 26. 
| 27. 
| 28. 
| 29. 
| 30. 
|
Задания 31 -40.
Сделать чертеж и вычислить площадь плоской фигуры, ограниченной линиями.
| 31.
| 
| 36.
| 
| | 32.
| 
| 37.
| 
| | 33.
| 
| 38.
| 
| | 34.
| 
| 39.
| 
| | 35.
| 
| 40.
| 
|
Задания 41-50.
| 41.
| В партии из шести деталей вероятность того, что деталь стандартная 0,7. Наудачу отобраны три детали. Составить закон распределения случайной величины Х – числа стандартных деталей среди отобранных. Найти числовые характеристики М (Х), D (Х),  (Х). (Х).
| | 42.
| Вероятность отказа прибора за время истечения на надежность равна 0,2. Построить закон распределения случайной величины Х - числа отказавших приборов, если испытанию будут подвергнуты четыре прибора. Найти числовые характеристики М (Х), D (Х),  (Х). (Х).
| | 43.
| Игральная кость брошена три раза. Написать ряд распределения случайной величины Х – числа выпадений шестерки. Найти числовые характеристики М (Х), D (Х),  (Х). (Х).
| | 44.
| Рабочий обслуживает три станка. Вероятность того, что в течение часа станок не потребует внимания рабочего– 0,8. Составить ряд распределения случайной величины Х – числа станков, которые не потребуют внимания рабочего в течение часа. Найти числовые характеристики М (Х), D (Х),  (Х). (Х).
| | 45.
| Производится три независимых опыта, в каждом из которых событие А появляется с вероятностью 0,4. Построить ряд распределения случайной величины Х – числа появлений события А. Найти числовые характеристики М (Х), D (Х),  (Х). (Х).
| | 46.
| Вероятность того, что студент найдет в справочнике нужную ему формулу, равна 0,4. Студент просмотрел четыре справочника. Построить ряд распределения числа справочников, в которых студент найдет нужную формулу. Найти числовые характеристики М (Х), D (Х),  (Х). (Х).
| | 47.
| Приобретено четыре лотерейных билета. Составить ряд распределения числа лотерейных билетов, на которые выпадут выигрыши, если вероятность выигрыша по одному билету 0,3. Найти числовые характеристики М (Х), D (Х),  (Х). (Х).
| | 48.
| Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при одном выстреле равна 0,3. Построить ряд распределения числа попаданий. Найти числовые характеристики М (Х), D (Х),  (Х). (Х).
| | 49.
| Баскетболист делает два штрафных броска. Вероятность попадания в корзину при одном броске 0,6. Составить ряд распределения случайной величины Х – числа попаданий мяча в корзину. Найти числовые характеристики М (Х), D (Х),  (Х). (Х).
| | 50.
| В некотором цехе брак составляет 5% всех изделий. Составить ряд распределения числа бракованных изделий из шести взятых наугад. Найти числовые характеристики М (Х), D (Х),  (Х). (Х).
|
Задания 51 - 60.
При изучении случайной величины Х в результате n независимых наблюдений получили выборку. Необходимо:
1. Построить дискретное статистическое распределение для этой выборки, а также полигон относительных частот.
2. Найти: выборочную среднюю  и среднее квадратическое отклонение и среднее квадратическое отклонение  ; моду ; моду  . .
| 51.
| 6, 10, 12, 2, 14, 12, 14, 12, 16, 4, 12, 14, 12, 16, 12, 10, 4, 6, 14, 6, 8, 12, 16, 8, 12, 8, 10, 16, 8, 10, 14, 10, 12, 12, 14, 16,12, 14, 12, 16, 4, 12, 14, 4, 6, 14, 6, 8, 12, 16.
| | 52.
| 25, 15, -5, 15, -10, 15, -15, -5, 10, 15, -10, -5, 15, -5, 5, 15,
-10, 5, -5, -5, -5, 10, 5, 10, 5, 10, -5, 10, 15, 10, 15, 20, 25, -5, -10, -15, 25, 15, -5, 15, -10, 15, -15, -5, 10, 15, 10, 15, 20, 25.
| | 53.
| 4, 32, 4, 20, 12, 4, 16, 20, 12, 20, 12, 28, 12, 20, 20, 20, 4, 24, 8, 20, 24, 16, 8, 8, 8, 20, 8, 8, 16, 8, 12, 8, 8, 16, 16, 8, 8, 12, 8, 12, 16, 20, 20, 24, 28, 28, 16, 28, 16, 28.
| | 54.
| 40, 5, 5, 25, 5, 15, 5, 30, 5, 15,5, 20, 5, 5, 20, 5, 25, 5, 10, 10, 25, 30, 25, 10, 35, 10, 25, 10, 30, 25, 25, 30, 10, 40, 10, 10, 15, 15, 40, 15, 15, 20, 20, 25, 25, 25, 30, 30, 35, 35.
| | 55.
| 30, 6, 24, 24, 24, 36, 18, 30, 30, 6, 48, 6, 36, 6, 30, 36, 6, 18, 24, 6, 42, 6, 6, 42, 6, 12, 12, 24, 30, 12, 42, 12, 48, 12, 12, 12, 18, 18, 18, 24,18, 24, 30, 36, 36, 12, 12, 36, 36, 12.
| | 56.
| 56, 7, 7, 14,, 14, 21, 21, 7, 7, 21, 28, 35, 28, 21, 21, 28, 28, 35, 35, 35, 42, 35, 42, 42, 42, 49, 7, 7, 7, 49, 7, 7, 49, 56, 56, 21, 21, 56,14, 7, 14, 14, 56, 14.
| | 57.
| 8, 40, 48, 8, 8, 16, 16, 8, 16, 32, 16, 16, 32, 16, 32, 16, 32, 16, 24, 16, 24, 24, 32, 64, 32, 8, 32, 8, 8, 32, 32, 40, 40, 8, 8, 40, 8, 16, 48, 56, 56, 16, 16, 56, 64, 64, 32, 32,64, 24, 32, 64.
| | 58.
| 17, 24, 24, 3, 3, 10, 10, 17, 17, 3, 3, 17, 52, 17, 24, 24, 31, 31, 31, 3, 10, 10, 31, 31, 38, 38, 38, 3, 3, 3, 38, 17, 17, 38, 38, 3, 38, 38, 45, 45, 10, 10, 45, 45, 45, 24, 24, 31, 31, 45.
| | 59.
| 28, 28, 4, 4, 28, 34, 34, 4, 4, 22, 22, 4, 10, 10, 28, 28, 10, 10, 22, 28, 10, 34, 40, 10, 10, 28, 46, 28, 10, 16, 16, 46, 16, 16, 28, 28, 16, 16, 22, 16, 16, 22, 28, 28, 34, 40, 16, 16, 40, 40.
| | 60.
| 65, 65, 75, 75, 5, 15, 65, 25, 5, 75, 5, 15, 75, 25, 25, 25, 35, 65, 65, 65, 35, 55, 65, 35, 45, 45, 45, 45, 55, 55, 55, 55, 65, 65, 65, 45, 45, 65, 65, 75, 75, 25, 35, 75, 45, 55, 75, 45, 75, 25.
|
Задание 61 – 70
Результаты измерений величин X и Y представлены таблицей.
1. Построить в прямоугольной системе координат заданные точки  . Убедиться, что величины X и Y связаны линейной зависимостью. . Убедиться, что величины X и Y связаны линейной зависимостью.
2. Составить уравнение регрессии  на на  . Построить полученную прямую. . Построить полученную прямую.
3. Найти коэффициент корреляции  , оценить тесноту связи, найти ошибку , оценить тесноту связи, найти ошибку  коэффициента корреляции. коэффициента корреляции.
| 61.
| x
|
|
|
|
|
|
|
|
|
|
| | y
| 15,1
| 16,9
|
| 21,1
| 16,5
| 16,5
| 26,3
| 22,3
| 26,3
| 15,3
| | 62.
| x
|
|
|
|
|
|
|
|
|
|
| | y
| 17,1
| 18,2
| 16,9
| 19,4
| 20,1
| 24,0
| 23,1
| 19,0
| 17,5
| 18,0
| | 63.
| x
|
|
|
|
|
|
|
|
|
|
| | y
| 27,9
| 22,0
| 30,5
| 25,4
| 24,1
| 34,0
| 35,2
| 39,2
| 29,7
| 28,0
| | 64.
| x
|
|
|
|
|
|
|
|
|
|
| | y
| 22,0
| 16,9
| 20,0
| 28,5
| 17,0
| 26,5
| 27,0
| 30,1
| 27,9
| 18,0
| | 65.
| x
|
|
|
|
|
|
|
|
|
|
| | y
| 17,0
| 13,4
| 15,2
| 18,2
| 22,5
| 20,0
| 25,0
| 23,0
| 18,4
| 14,9
| | 66.
| x
|
|
|
|
|
|
|
|
|
|
| | y
| 21,0
| 22,9
| 26,9
| 30,9
| 25,1
| 33,0
| 23,5
| 33,2
| 22,1
| 31,2
| | 67.
| x
|
|
|
|
|
|
|
|
|
|
| | y
| 7,9
| 11,0
| 21,0
| 8,5
| 14,2
| 20,0
| 24,1
| 17,1
| 15,0
| 23,9
| | 68.
| x
|
|
|
|
|
|
|
|
|
|
| | y
| 6,0
| 8,1
| 14,5
| 10,5
| 16,5
| 1,0
| 12,1
| 18,5
| 20,2
| 22,0
| | 69.
| x
|
|
|
|
|
|
|
|
|
|
| | y
| 6,5
| 5,0
| 8,3
| 7,4
| 4,0
| 7,2
| 6,5
| 8,4
| 4,0
| 10,0
| | 70.
| x
|
|
|
|
|
|
|
|
|
|
| | y
| 9,9
| 12,0
| 8,1
| 16,5
| 24,5
| 22,0
| 18,2
| 20,5
| 18,5
| 14,2
|
|
| 3. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ И РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
3.1 Задания типа 1-10
Дана система линейных уравнений  Решить по формулам Крамера.
Решение.
Дадим некоторые определения и понятия необходимые для решения задачи.
Прямоугольная таблица из чисел или иных математических объектов, содержащая m строк и n столбцов, называется матрицей. Обозначается заглавными буквами: А, В, С, D,… Общий вид матрицы
Решить по формулам Крамера.
Решение.
Дадим некоторые определения и понятия необходимые для решения задачи.
Прямоугольная таблица из чисел или иных математических объектов, содержащая m строк и n столбцов, называется матрицей. Обозначается заглавными буквами: А, В, С, D,… Общий вид матрицы
 .
Размерность матрицы m×n.
Если число строк n матрицы равно числу столбцов, то такая матрица называется квадратной и n ее порядок.
Пример квадратной матрицы второго порядка .
Размерность матрицы m×n.
Если число строк n матрицы равно числу столбцов, то такая матрица называется квадратной и n ее порядок.
Пример квадратной матрицы второго порядка  .
Пример квадратной матрицы третьего порядка .
Пример квадратной матрицы третьего порядка  .
Определителем матрицы второго порядка называется число, равное разности между произведением чисел, образующих главную диагональ, и произведением чисел, стоящих на побочной диагонали, можно встретить следующие обозначения определителя: .
Определителем матрицы второго порядка называется число, равное разности между произведением чисел, образующих главную диагональ, и произведением чисел, стоящих на побочной диагонали, можно встретить следующие обозначения определителя:  ; ;  ; ;  ; detA (детерминант). ; detA (детерминант).
 .
Пример: .
Пример:  .
Определителем матрицы третьего порядка называется число или математическое выражение, вычисляемое по следующему правилу .
Определителем матрицы третьего порядка называется число или математическое выражение, вычисляемое по следующему правилу
 Наиболее простым способом вычисления определителя третьего порядка является дописывание снизу определителя двух первых строк.
В образованной таблице чисел перемножаются элементы, стоящие на главной диагонали и на диагоналях параллельных главной, знак результата произведения не изменяется. Следующим этапом вычислений является аналогичное перемножение элементов, стоящих на побочной диагонали и на параллельных ей. Знаки у результатов произведений меняются на противоположные. Затем складываем полученные шесть слагаемых.
Пример: Наиболее простым способом вычисления определителя третьего порядка является дописывание снизу определителя двух первых строк.
В образованной таблице чисел перемножаются элементы, стоящие на главной диагонали и на диагоналях параллельных главной, знак результата произведения не изменяется. Следующим этапом вычислений является аналогичное перемножение элементов, стоящих на побочной диагонали и на параллельных ей. Знаки у результатов произведений меняются на противоположные. Затем складываем полученные шесть слагаемых.
Пример:
 Минором элемента Минором элемента  определителя n –го порядка называется определитель (n -1) –го порядка, полученный из данного определителя вычеркиванием i –ой строки и j –го столбца. Минор элемента определителя n –го порядка называется определитель (n -1) –го порядка, полученный из данного определителя вычеркиванием i –ой строки и j –го столбца. Минор элемента  определителя обозначается определителя обозначается  .
Алгебраическим дополнением элемента .
Алгебраическим дополнением элемента  определителя n –го порядка называется его минор определителя n –го порядка называется его минор  , взятый со знаком , взятый со знаком  . Алгебраическое дополнение элемента . Алгебраическое дополнение элемента  обозначается обозначается  . Следовательно, . Следовательно,  .
Правило вычисления определителя любого порядка: определитель любого порядка n равен сумме произведений элементов какой–либо строки (или столбца) на их алгебраические дополнения.
Найдем определитель третьего порядка путем разложения по элементам первой строки: .
Правило вычисления определителя любого порядка: определитель любого порядка n равен сумме произведений элементов какой–либо строки (или столбца) на их алгебраические дополнения.
Найдем определитель третьего порядка путем разложения по элементам первой строки:
 .
Аналогично можно вычислить определитель третьего порядка, разложив по любой строке или столбцу. Удобно раскладывать определитель по той строке (или столбцу), в которой содержится больше нулей.
Пример: .
Аналогично можно вычислить определитель третьего порядка, разложив по любой строке или столбцу. Удобно раскладывать определитель по той строке (или столбцу), в которой содержится больше нулей.
Пример:  .
Рассмотрим систему из трех уравнений с тремя неизвестными (m=n): .
Рассмотрим систему из трех уравнений с тремя неизвестными (m=n):
 Матрица
Матрица  , составленная из коэффициентов, стоящих перед неизвестными, называется матрицей системы или главной матрицей. , составленная из коэффициентов, стоящих перед неизвестными, называется матрицей системы или главной матрицей.
 - матрица-столбец неизвестных, - матрица-столбец неизвестных,  - матрица-столбец свободных членов.
Теорема Крамера. Если определитель матрицы системы n -го порядка отличен от нуля - матрица-столбец свободных членов.
Теорема Крамера. Если определитель матрицы системы n -го порядка отличен от нуля  , то система совместна и имеет единственное решение, которое определяется по формулам , то система совместна и имеет единственное решение, которое определяется по формулам  . .  - вспомогательный определитель, полученный из главного путем замены столбца коэффициентов при хi на столбец свободных членов. В частности, для матрицы 3-го порядка - вспомогательный определитель, полученный из главного путем замены столбца коэффициентов при хi на столбец свободных членов. В частности, для матрицы 3-го порядка  .
Вернемся к нашей системе, решим ее по формулам Крамера. .
Вернемся к нашей системе, решим ее по формулам Крамера.
| 1) Вычислим главный определитель системы и вспомогательные определители.
Главный определитель системы составляется из коэффициентов при неизвестных:
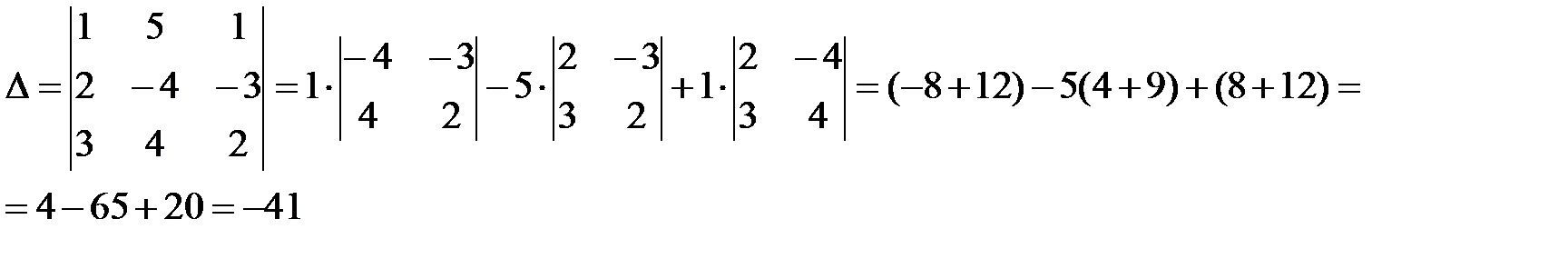
Определитель системы отличен от нуля, следовательно, система совместна и имеет единственное решение.
Вычислим вспомогательные определители, чтобы их получить, заменим соответственно первый, второй или третий столбец определителя системы столбцом свободных членов. Определители вычисляем разложением по первой строке:
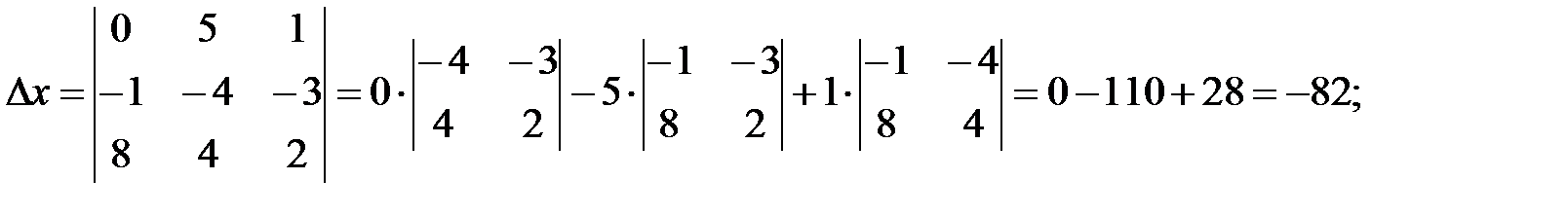

 . .
По правилу Крамера:  , ,  , ,  . .
Ответ: x=2, y=-1, z=3.
Чтобы проверить правильность решения, нужно подставить эти числа в каждое уравнение данной системы и получить верные тождества.
Задания типа 11-20
Если каждому значению переменной х из множества Х по некоторому правилу поставлено в соответствие единственное вполне определенное значение y, то переменную y называют функцией от х.
Записывают  или или  . Говорят ещё, что функция отображает множество Х на множество Y. . Говорят ещё, что функция отображает множество Х на множество Y.
Множество Х называется областью определения функции и обозначается  . Множество всех . Множество всех  называется множеством значений функции и обозначается называется множеством значений функции и обозначается  . .
х – независимая переменная величина или аргумент, y – функция или зависимая переменная.
Число А называется пределом функции 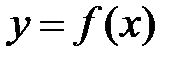 при при  , если для любого положительного числа , если для любого положительного числа  найдется такое положительное число найдется такое положительное число 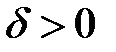 , что для всех , что для всех  , удовлетворяющих неравенству , удовлетворяющих неравенству  , выполняется неравенство , выполняется неравенство  . Записывают . Записывают  . .
Аналогично:
 , если , если  при при  , N – произвольное положительное число. , N – произвольное положительное число.
 , если , если  при при  , где М – произвольное сколько угодно большое положительное число. В этом случае функция , где М – произвольное сколько угодно большое положительное число. В этом случае функция 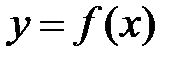 называется бесконечно большой величиной при называется бесконечно большой величиной при  . .
Если  , то функция , то функция 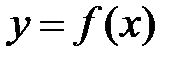 называется бесконечно малой величиной при называется бесконечно малой величиной при  . .
Простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A ≠ 0
 . .
Практическое вычисление пределов основывается на следующих теоремах.
Если существуют конечные  и и  , то , то
1) 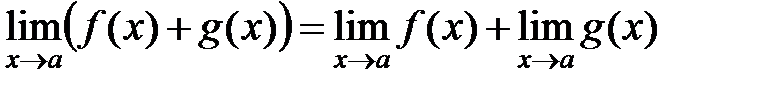
2) 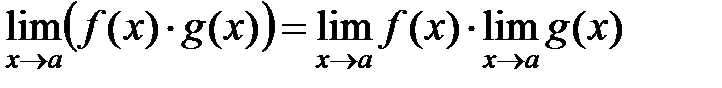
3)  (с – константа) (с – константа)
4)  , ( , ( ). ).
Используются также следующие пределы:
 ; ;  - первый замечательный предел; - первый замечательный предел;
 ; ;  - второй замечательный предел. Число е≈2,71828. - второй замечательный предел. Число е≈2,71828.
С числом е связана система логарифмов, более удобная, чем десятичная.
 - называется натуральный логарифм. - называется натуральный логарифм.
Число е называют ещё неперовым числом (по имени одного из первых изобретателей логарифмических таблиц Непера (1550-1617)). Показательная функция  играет большую роль при изучении различных явлений в механике (теория колебаний), в электротехнике, радиотехнике. Функцию играет большую роль при изучении различных явлений в механике (теория колебаний), в электротехнике, радиотехнике. Функцию  часто называют экспонентой и обозначают часто называют экспонентой и обозначают  . .
Разберем подобные примеры из контрольной работы. Найти пределы, не пользуясь правилом Лопиталя:
а)  б) б) 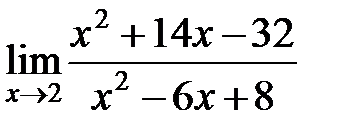
Обычно для отыскания предела используют теоремы о пределах. Из этих теорем следует: если предельная точка входит в область определения функции, стоящей под знаком предела, то для его отыскания нужно найти значение функции в этой точке.
 . . 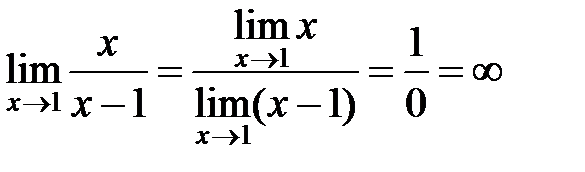
Но часто теоремы о пределах применить нельзя. Это бывает в случаях, так называемых, неопределенных выражений:  . .
Рассмотрим основные способы раскрытия неопределенностей на указанных выше примерах.
а) 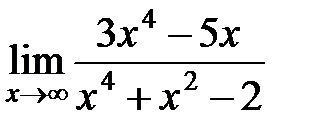
Решение. Теорему о пределе частного применять нельзя, т.к. числитель и знаменатель неограниченно возрастают при  . Имеем неопределенность вида . Имеем неопределенность вида  . В подобных примерах числитель и знаменатель дроби целесообразно разделить на высшую степень переменной. В нашем примере разделим числитель и знаменатель на . В подобных примерах числитель и знаменатель дроби целесообразно разделить на высшую степень переменной. В нашем примере разделим числитель и знаменатель на  , затем перейдем к пределу. , затем перейдем к пределу.
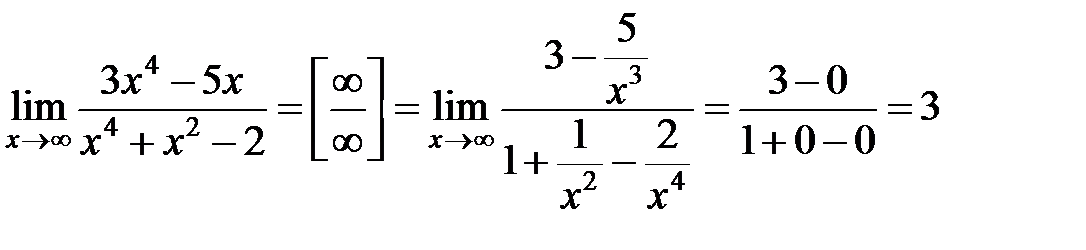
б) 
Решение. Подставляя х=2 в числитель и знаменатель дроби получим неопределенность вида  . В подобных примерах, когда числитель и знаменатель многочлены, их необходимо разложить на множители, после этого дробь сократить и прейти к пределу. Для разложения на множители квадратного трехчлена используем формулу . В подобных примерах, когда числитель и знаменатель многочлены, их необходимо разложить на множители, после этого дробь сократить и прейти к пределу. Для разложения на множители квадратного трехчлена используем формулу  , где х1,х2 – корни соответствующего квадратного уравнения , где х1,х2 – корни соответствующего квадратного уравнения
 . .
Задания типа 21-30
Производная функции.
Пусть имеем функцию  , определенную на некотором промежутке. Рассмотрим два значения аргумента: исходное x0 и новое x. Разность , определенную на некотором промежутке. Рассмотрим два значения аргумента: исходное x0 и новое x. Разность  называется приращением аргумента x в точке x0 и обозначается называется приращением аргумента x в точке x0 и обозначается  . .
Разность  называется приращением функции называется приращением функции  в точке x0 и обозначается символом Δy. в точке x0 и обозначается символом Δy.
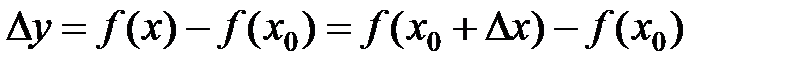
Производной функции  называется предел отношения приращения функции Δy к приращению аргумента Δx, когда последнее произвольным образом стремится к нулю. называется предел отношения приращения функции Δy к приращению аргумента Δx, когда последнее произвольным образом стремится к нулю. 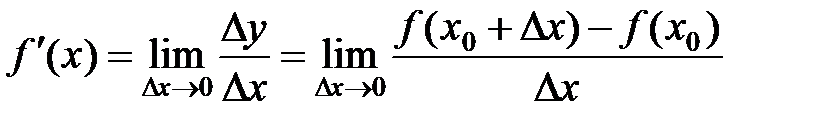
Заметим, что для одной и той же функции производная в различных точках x может принимать различные значения, т.е. производную можно рассматривать как функцию аргумента x. Эта функция обозначается f '(x).
Производная обозначается символами  . Операция нахождения производной от функции f(x) называется дифференцированием этой функции. . Операция нахождения производной от функции f(x) называется дифференцированием этой функции.
Правила дифференцирования:
1. 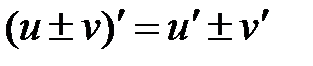
2.  ; ;  с-const с-const
3.  ; ;  с-const с-const
4.  , если , если 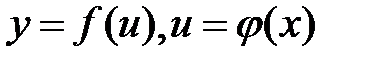 , т.е. , т.е. 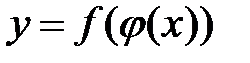
5.  , если , если  и и  - взаимно обратные функции. - взаимно обратные функции.
Формулы дифференцирования.
Примеры:
Пользуясь правилами и формулами дифференцирования, найти производные следующих функций:
1) 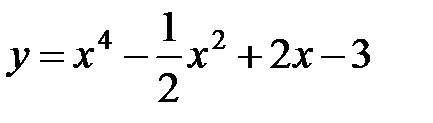
Воспользуемся формулой дифференцирования степенной функции  : :
 . .
2)  . .
Воспользуемся формулой производной произведения 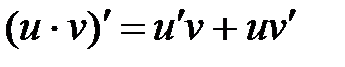
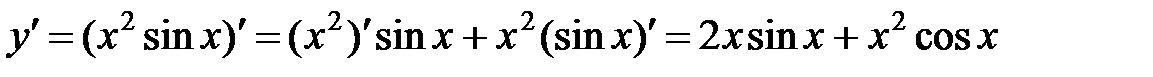
Экстремумы функции.
Точка  называется точкой максимума функции называется точкой максимума функции  , если значение , если значение  является наибольшим в некоторой окрестности этой точки. является наибольшим в некоторой окрестности этой точки.
Точка  называется точкой минимума функции называется точкой минимума функции  , если значение , если значение  является наименьшим в некоторой окрестности этой точки. является наименьшим в некоторой окрестности этой точки.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках – экстремумами функции.
Теорема (Ферма – необходимое условие экстремума). Если  - точка экстремума для функции - точка экстремума для функции  , то в этой точке производная функции либо равна нулю , то в этой точке производная функции либо равна нулю  , либо не существует. , либо не существует.
Точки области определения функции 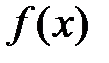 , в которых ее производная не существует или равна нулю, называются критическими точками функции. , в которых ее производная не существует или равна нулю, называются критическими точками функции.
В силу теоремы Ферма экстремумы функции находятся среди ее критических точек.
Первое достаточное условие экстремума. Если при переходе (слева направо) через критическую точку  производная производная  меняет знак с (+) на (-), то точка меняет знак с (+) на (-), то точка  является точкой максимума; если с (-) на (+), то точкой минимума; если знака не меняет, то экстремума нет. является точкой максимума; если с (-) на (+), то точкой минимума; если знака не меняет, то экстремума нет.
Второе достаточное условие экстремума. Пусть в точке  производная равна нулю производная равна нулю  , а вторая производная , а вторая производная  . Тогда, если . Тогда, если  , то , то  - точка минимума; если - точка минимума; если  , то , то  - точка максимума. - точка максимума.
Пример.
Найти экстремумы функции, интервалы возрастания и убывания
 . .
Решение.
Найдем производную  и решим уравнение и решим уравнение  . .
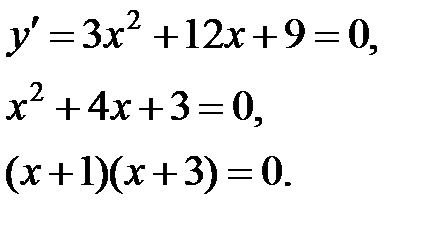
Производная обращается в ноль при  или или  . .
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|
 называется точкой минимума функции
называется точкой минимума функции  , если значение
, если значение  является наименьшим в некоторой окрестности этой точки.
является наименьшим в некоторой окрестности этой точки.




