|
|
Понятие неопределенного интегралаВ дифференциальном исчислении решается задача: по данной функции Функция
Например, первообразной функции
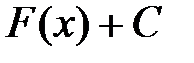 для для 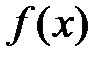 называется неопределенным интегралом от функции называется неопределенным интегралом от функции 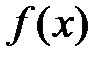 и обозначается символом и обозначается символом  , т.е. , т.е.  , ,
х – переменная интегрирования; Операция нахождения неопределенного интеграла от функции Свойства неопределенного интеграла. 1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная интеграла равна подынтегральной функции 2. 3. 4. 5. Инвариантность формулы интегрирования. Если Таблица основных неопределенных интегралов. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11 14.
16.
Метод непосредственного интегрирования Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. Примеры: 1. 2.
3.
Определенный интеграл. Площадь криволинейной трапеции Пусть функция f (x) определена на отрезке [ а; b ]. Разобьем этот отрезок на n частей произвольным образом точками х 0 = а < x 1 < x 2 < …< x n = b. Пусть
Определенным интегралом от функции f (x) на отрезке [ а; b ] называется предел последовательности интегральных сумм при условии, что длина наибольшего из частичных отрезков
Свойства определенного интеграла
Вычисление определенного интеграла. Формула Ньютона – Лейбница. Определенный интеграл от непрерывной функции f (x) равен разности значений ее первообразной F (x) при х=b и х=а, где а и b нижний и верхний пределы интегрирования, т.е. имеет место формула
Пример: Вычисление площади плоской фигуры
Пример 1. Вычислить площадь фигуры, ограниченной линиями Решение. Построим фигуру, площадь которой надо найти. Графиком функции Тогда:
Если фигура ограничена линиями у = f 1(x) и у = f 2(x), где f 2(x) ≥ f 1(x), и прямыми х=а и х= b, то ее площадь определяется по формуле
Пример 2. Найти площадь фигуры, ограниченной линиями:
Решим уравнение:
Тогда
Задания типа 41-50
Основы теории вероятностей Математическая наука, которая изучает закономерности массовых событий, называется теорией вероятности. Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать. Науку, которая использует теорию вероятностей для обработки численных единиц информации как результатов эксперимента, называют математической статистикой. Последовательность операций, выполняемых с соблюдением конкретного комплекса условий, называют экспериментом или испытанием. Результат испытания называют событием. Пример. Брошена монета – испытание; появление герба – событие. Наблюдаемые нами события можно подразделить на следующие три вида: достоверные; невозможные; случайные. Достовернымназывают событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S. Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий S. Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти в зависимости от действия многочисленных факторов, учесть которые исследователь не в силах. Случайные события обозначают символами А, В, С. Пример. В урне находятся 10 одинаковых шаров, пронумерованных от 1 до 10. Наугад берется один шар. Возможны следующие события: 1) появление шара с номером от 1 до 10 – событие достоверное; 2) появление шара с номером 12 – событие невозможное; 3) появление шара с номером 2 – событие случайное. Виды случайных событий. События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. События называют совместными, если появление одного из них не исключает появление других событий в одном и том же испытании. События называют единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием. События называют равновозможными, если есть основание считать, что ни одно из этих событий не является более возможным, чем другие. Совокупность всех единственно возможных событий испытания называют полной группой событий. Пример. Стрелок произвел 2 выстрела. Полная группа событий: Событие Событие Событие Противоположныминазывают два единственно возможных события образующих полную группу событий. Обозначение: Пример. Монета брошена 1 раз. События: Брошена игральная кость. События:   Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...  ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования...  Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот...  ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|