|
|
Теорема о четырех точках трапеции ⇐ ПредыдущаяСтр 5 из 5
Обозначим через  и и  середины оснований середины оснований  и и 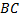 трапеции трапеции 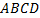 ; ;  – точка пересечения ее диагоналей, – точка пересечения ее диагоналей,  – точка пересечения продолжений боковых сторон. – точка пересечения продолжений боковых сторон. Заметим, что точки  , ,  и и  лежат на одной прямой. Это следует из подобия треугольников лежат на одной прямой. Это следует из подобия треугольников  и и  . В каждом из них отрезки . В каждом из них отрезки  и и  соответственно являются медианами, а значит, они делят угол при вершине соответственно являются медианами, а значит, они делят угол при вершине  на одинаковые части. на одинаковые части. Точно так же на одной прямой расположены точки  , ,  и и  . (Здесь это следует из подобия треугольников . (Здесь это следует из подобия треугольников  и и  .) Значит, все четыре токи .) Значит, все четыре токи  , ,  , ,  и и  лежат на одной прямой, т.е. прямая лежат на одной прямой, т.е. прямая  проходит через проходит через  и и  . .
Определение: Квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин его катетов. Доказательство: Проведем высоту BH из угла B к стороне AC. Δ Билет 36. Теорема синусов Определение: Стороны треугольника пропорциональны синусам противолежащих углов. Доказательство: Пусть дан треугольник со сторонами Билет 37. Теорема косинусов
 . Из вершины . Из вершины 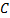 на сторону на сторону  опущена высота опущена высота  . Из треугольника . Из треугольника  следует, что следует, что 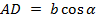 и и  Запишем теорему Пифагора для двух прямоугольных треугольников Запишем теорему Пифагора для двух прямоугольных треугольников  и и  : : (1) (1)
Приравниваем правые части уравнений (1) и (2):
Окружность Аполлония –геометрическое место точек плоскости, отношение расстояний от которых до двух заданных точек – величина постоянная. Пусть на плоскости даны две точки Свойства окружности Апполония 1) Радиус окружности Апполония равен 2) Отрезок между точкой на окружности и точкой пересечения ее с прямой Билет 39. Теорема Чевы Определение: В произвольном треугольнике а) прямые
 (Условие Чевы) (Условие Чевы)
Доказательство: Доказать теорему Чевы проще всего, заменив отношения отрезков в условии Чевы на отношение площадей:

Следовательно,
Точно так же получим, что Теперь осталось только перемножить эти три равенства:
Обратная теорема Чевы Пусть Билет 40. Построение касательной к окружности Касательную из точки 1. На отрезке 2. Точки 3. Отрезки Билет 41. Выражение координат середины отрезка через координаты его концов
Билет 42. Радиус вписанной в треугольник и описанной вокруг него окружности Исходя из формулы Радиус описанной окружности *Примечание: к сожалению, эксперты Волшебной Формулы не смогли найти доказательство данной теоремы. Билет 43. Вывод формулы окружности Выведем формулу окружностью с радиусом Билет 44. Правильный многоугольник – такой многоугольник, стороны которого равны. Построение квадрата Построим на плоскости окружность и проведем ее диаметр. Затем построим другой диаметр, перпендикулярный** предыдущему. Соединив точки пересечения диаметра, мы получаем квадрат. Для того чтобы получить квадрат со стороной ** см. Билет 28.
Схема построения квадрата:
Построение правильного шестиугольника со стороной Построим окружность с радиусом Схема построения правильного шестиугольника:
Билет 45.   ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала...  Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом...  Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...  Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|