|
|
Признаки равенства прямоугольных треугольниковСм. Билет 6. Примечание: при доказательстве признаков равенства прямоугольных треугольников следует принимать во внимание, что один прямой угол у них итак равен. Билет 17.
I.
Доказательство: Пусть 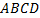 – данный четырехугольник, – данный четырехугольник, 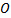 – точка пересечения диагоналей данного параллелограмма. – точка пересечения диагоналей данного параллелограмма. Δ 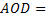 Δ Δ  по первому признаку равенства треугольников ( по первому признаку равенства треугольников ( по условию теоремы, по условию теоремы,  , как вертикальные углы). Следовательно, , как вертикальные углы). Следовательно,  . А они являются внутренними накрест лежащими для прямых . А они являются внутренними накрест лежащими для прямых  и и 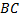 и секущей и секущей  . По признаку параллельности прямых прямые . По признаку параллельности прямых прямые  и и 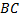 параллельны. Так же доказываем, что параллельны. Так же доказываем, что  и и  тоже параллельны. По определению данный четырехугольник параллелограмм. Теорема доказана. тоже параллельны. По определению данный четырехугольник параллелограмм. Теорема доказана.
II.
Доказательство: Пусть 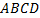 – данный четырехугольник. – данный четырехугольник.  и и  . . Тогда Δ 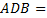 Δ Δ  по первому признаку равенства треугольников ( по первому признаку равенства треугольников ( , как внутренние накрест лежащие между прямыми , как внутренние накрест лежащие между прямыми  и и 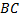 и секущей и секущей  , ,  по условию, по условию,  – общая). – общая). Следовательно,  , а эти углы являются внутренними накрест лежащими для прямых , а эти углы являются внутренними накрест лежащими для прямых  и и  и секущей и секущей  . По теореме признаке параллельности прямых . По теореме признаке параллельности прямых  и и  параллельны. Значит, параллельны. Значит, 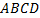 – параллелограмм. Теорема доказана. – параллелограмм. Теорема доказана.
III.
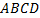 . .  и и  . Проведем диагональ DB. Сумма углов четырех угольника равна сумме углов треугольников . Проведем диагональ DB. Сумма углов четырех угольника равна сумме углов треугольников  и и  . По теореме о сумме углов треугольника, получаем: . По теореме о сумме углов треугольника, получаем: . Так как противолежащие углы в четырехугольнике равны, то . Так как противолежащие углы в четырехугольнике равны, то  и и  . . Углы  и и  являются внутренними односторонними для прямых являются внутренними односторонними для прямых  и и 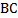 и секущей и секущей  , их сумма равна , их сумма равна 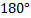 , поэтому из следствия к теореме о признаке параллельности прямых, прямые , поэтому из следствия к теореме о признаке параллельности прямых, прямые  и и 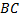 параллельны. Так же доказывается, что параллельны. Так же доказывается, что  . Таким образом, четырехугольник . Таким образом, четырехугольник 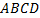 – параллелограмм по определению. Теорема доказана. – параллелограмм по определению. Теорема доказана.
Билет 18. Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.
I.
Доказательство: Пусть 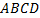 – параллелограмм. Диагональ – параллелограмм. Диагональ  делит его на два треугольника: Δ делит его на два треугольника: Δ  и Δ и Δ  . Эти треугольники равны по стороне и двум углам ( . Эти треугольники равны по стороне и двум углам (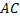 – общая, – общая,  , , 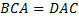 – как накрест лежащие). Отсюда, – как накрест лежащие). Отсюда,  . Теорема доказана. . Теорема доказана.
II. В параллелограмме противоположные углы равны. III.
Доказательство: Пусть 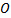 – точка пересечения диагоналей параллелограмма ABCD. Δ – точка пересечения диагоналей параллелограмма ABCD. Δ  Δ Δ  по стороне и двум углам ( по стороне и двум углам ( как вертикал., как вертикал.,  , ,  как накрест лежащие). Отсюда как накрест лежащие). Отсюда  , , 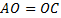 , ч. т. д. , ч. т. д.
Билет 19. Прямоугольником называют параллелограмм, у которого все углы прямые
Доказательство: Рассмотрим прямоугольник 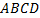 . . Δ  Δ Δ  по двум катетам. Отсюда диагонали по двум катетам. Отсюда диагонали  Обратное утверждение (признак): Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником. Билет 20. Ромбом называется параллелограмм, у которого все стороны равны.
Доказательство: Рассмотрим ромб  , требуется доказать, что , требуется доказать, что 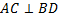 , и что диагонали ромба делят его углы пополам. Докажем, например, что , и что диагонали ромба делят его углы пополам. Докажем, например, что  . Т. к. . Т. к.  , то Δ , то Δ  – равнобедренный. Так как ромб – параллелограмм, то точкой пресечения его диагонали делятся пополам, значит – равнобедренный. Так как ромб – параллелограмм, то точкой пресечения его диагонали делятся пополам, значит 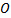 – медиана равнобедренного треугольника – медиана равнобедренного треугольника  , а значит его биссектриса и высота. Поэтому , а значит его биссектриса и высота. Поэтому 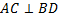 и и  . .
Теорема Менелая
 , , 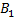 , ,  лежат соответственно на сторонах лежат соответственно на сторонах 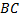 , ,  и и  треугольника Δ треугольника Δ  или на их продолжениях, то они лежат на одной прямой тогда и только тогда, когда или на их продолжениях, то они лежат на одной прямой тогда и только тогда, когда  . .
Доказательство: Проведем через точку Билет 22. Средняя линия треугольника Средняя линия треугольника – отрезок, соединяющий середины двух сторон этого треугольника. Обладает следующими свойствами: 1) Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине. 2) При проведении всех трех средних линий образуются 4 равных треугольника, подобных исходному с коэффициентом 0,5. 3) Средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четверти площади исходного треугольника. Средняя линия трапеции Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Обладает следующими свойствами: 1) средняя линия параллельна основаниям трапеции и равна их полусумме; 2) середины сторон равнобедренной трапеции являются вершинами ромба.
Определение: Доказательство: Расстояние между началом координат и заданной точкой:
Билет 24. Окружностью называется геометрическое место точек, равноудаленных от заданной. Длина окружности: Длина дуги окружности Так как длина окружности равна Билет 25.   Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам...  Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...  Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...  ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|