|
|
Первый признак равенства треугольниковОпределение: Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
 и Δ и Δ  , у которого , у которого  , ,  и и  . Так как . Так как  , то Δ , то Δ  можно наложить на Δ можно наложить на Δ  так, что вершина так, что вершина  совместится с вершиной совместится с вершиной  , а стороны , а стороны  и и 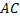 наложатся соответственно на лучи наложатся соответственно на лучи  и и  . Поскольку . Поскольку  , ,  , то точка , то точка  совместится с точкой совместится с точкой 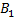 , а точка , а точка  – с точкой – с точкой  . Итак, Δ . Итак, Δ  и Δ и Δ  равны. равны.
Определение: Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Доказательство: Рассмотрим Δ
Определение: Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Доказательство: Рассмотрим Δ ** см. Билет 31.
На чертеже:
 , и секущая , и секущая  , пересекающая их, образует накрест лежащие углы , пересекающая их, образует накрест лежащие углы  и и  . Проведем перпендикуляр из точки . Проведем перпендикуляр из точки  к прямой к прямой  и из точки и из точки  к прямой к прямой  . Данные треугольники будут равны по углу и двум сторонам ( . Данные треугольники будут равны по углу и двум сторонам ( общ.), отсюда общ.), отсюда  . .
Теорема: Если две параллельные прямые пересечены секущей, то соответственные углы равны. Доказательство: Обратимся к рис. 7.1. Докажем, что соответственные углы, Теорема: Если две параллельные прямые пересечены секущей, сумма односторонних углов равна Доказательство: Обратимся к рис. 7.1. Докажем, что сумма односторонних углов, Билет 8. Часть плоскости, ограниченная окружностью, называется кругом. Площадь круга: Площадь кругового сектора Так как площадь круга равна Билет 9.
Пусть Выразим гипотенузу
Т. к. синус – отношение противолежащего катета к гипотенузе, то:
Аналогично,
Вывод формулы площади треугольника За основу возьмем формулу площади треугольника Так как синус по определению – это отношение противолежащего
 . Отсюда, . Отсюда,  . .
Подставив в исходную формулу, получаем: иными словами, * см. Билет 32. Билет 11. Нахождение гипотенузы, катета и острого угла прямоугольного треугольника по данным его второго катета и острому углу
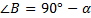 (по теореме о сумме углов треугольника**) (по теореме о сумме углов треугольника**)
** см. Билет 15. Билет 12. Теорема о сумме углов выпуклого многоугольника Определение: Сумма углов n-угольника равна Доказательство: Пусть Билет 13. Деление отрезка на
 – данный отрезок. Проведем из точки – данный отрезок. Проведем из точки  луч луч  , не содержащий отрезок , не содержащий отрезок  . Отложим от точки . Отложим от точки  на построенном луче равные отрезки: на построенном луче равные отрезки:  , ,   . Соединим точки . Соединим точки  и и  . Проведем через точки . Проведем через точки  , ,  прямые, параллельные* прямой прямые, параллельные* прямой 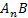 . Они пересекают отрезок . Они пересекают отрезок  в точках в точках 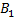 , ,    . Отрезки . Отрезки  , ,   – искомые отрезки. – искомые отрезки.
* см. Билет 45. Билет 14.
 где где 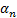 – величина угла правильного n-угольника. Эту величину можно найти по формуле – величина угла правильного n-угольника. Эту величину можно найти по формуле  (следствие из теоремы о сумме углов многоугольника**). Отсюда (следствие из теоремы о сумме углов многоугольника**). Отсюда  . Тогда сторона . Тогда сторона  ; а ; а  . Из . Из последней формулы выразим  . Подставим вместо . Подставим вместо  получившееся выражение: получившееся выражение:  . .
Рассмотрим несколько частных случаев: Для равностороннего треугольника: Для квадрата: Для правильного шестиугольника: ** см. Билет 12. Билет 15. Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки.
Определение: Сумма углов треугольника равна
 и и  равны как накрест лежащие. Аналогично, равны как накрест лежащие. Аналогично,  . Но углы . Но углы  , ,  и и  образуют развернутый угол, следовательно, их сумма равна образуют развернутый угол, следовательно, их сумма равна 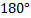 . тогда сумма соответствующих углов треугольника также равна . тогда сумма соответствующих углов треугольника также равна 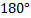 , ч. т. д. , ч. т. д.
Билет 16.   Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор...  Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...  ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры...  Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|