|
|
Свойства равнобедренного треугольникаСтр 1 из 5Следующая ⇒ Билет 1. Треугольник называется равнобедренным, если у него две стороны равны. Эти стороны называются боковыми, а третья сторона – основанием. Свойства равнобедренного треугольника 1) Углы при основании равны и являются острыми; 2) Медиана, проведенная к основанию, является биссектрисой и высотой. Теорема о свойстве медианы равнобедренного треугольника
 – равнобедренный, с основанием – равнобедренный, с основанием  , и , и  – медиана, проведенная к основанию. В треугольниках – медиана, проведенная к основанию. В треугольниках  и и  углы углы  и и  равны, как углы при основании равнобедренного, стороны равны, как углы при основании равнобедренного, стороны  и и 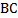 равны по определению равнобедренного треугольника, стороны равны по определению равнобедренного треугольника, стороны  и и  равны, потому что равны, потому что  – середина отрезка – середина отрезка  . Отсюда получаем, что Δ . Отсюда получаем, что Δ  Δ Δ  . .
Билет 2. Геометрическое место точек – это множество всех точек, удовлетворяющих определенным заданным условиям. 1) Срединный перпендикуляр любого отрезка есть геометрическое место точек, равноудаленных от концов этого отрезка. 2) Биссектриса угла есть геометрическое место точек, равноудаленных от его сторон. 3) Окружность есть геометрическое место точек, равноудаленных от ее центра. Теорема о геометрическом месте точек, равноудаленных от двух данных точек
 к к  — данные точки, — данные точки,  — прямая, проходящая через середину — прямая, проходящая через середину 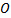 отрезка отрезка  перпендикулярно к нему. Любая точка перпендикулярно к нему. Любая точка 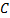 прямой прямой  находится на одинаковом расстоянии от точек находится на одинаковом расстоянии от точек  и и  , следует из равенства треугольников , следует из равенства треугольников  и и  . У этих треугольников углы при вершине . У этих треугольников углы при вершине 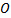 прямые, сторона прямые, сторона  общая, а общая, а  , так как , так как 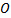 — середина отрезка — середина отрезка  . .
Билет 3. Углы, смежные с углами треугольника, называются внешними углами треугольника. Сумма внешних углов многоугольника всегда равна Теорема о внешнем угле треугольника
 – данный треугольник. Из теоремы о сумме углов треугольника, – данный треугольник. Из теоремы о сумме углов треугольника,  . Но . Но  — величина внешнего угла при вершине — величина внешнего угла при вершине 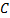 , значит, внешний угол равен , значит, внешний угол равен  . .
Билет 4. Прямые, на всем своем протяжении не имеющие точек пересечения, называются параллельными. Признаки параллельности прямых 1) Две прямые, параллельные третьей параллельны. 2) Если внутренние накрест лежащие* углы равны, то прямые параллельны. 3) Если сумма внутренних односторонних* углов равна 180°, то прямые параллельны. 4) Если соответственные* углы равны, то прямые параллельны. * см. Билет 7. Билет 5. Соотношения между прямыми и отрезками окружности Произведение отрезков пересекающихся хорд окружности равны. 2)
3)

4) Произведения отрезков секущих, проведенных из одной точки, равны:
Билет 8. Часть плоскости, ограниченная окружностью, называется кругом. Площадь круга: Площадь кругового сектора Так как площадь круга равна Билет 9.
Пусть Выразим гипотенузу
Т. к. синус – отношение противолежащего катета к гипотенузе, то:
Аналогично,
Вывод формулы площади треугольника За основу возьмем формулу площади треугольника Так как синус по определению – это отношение противолежащего
 . Отсюда, . Отсюда,  . .
Подставив в исходную формулу, получаем: иными словами, * см. Билет 32. Билет 11. Нахождение гипотенузы, катета и острого угла прямоугольного треугольника по данным его второго катета и острому углу
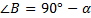 (по теореме о сумме углов треугольника**) (по теореме о сумме углов треугольника**)
** см. Билет 15. Билет 12. Билет 13. Деление отрезка на
 – данный отрезок. Проведем из точки – данный отрезок. Проведем из точки  луч луч  , не содержащий отрезок , не содержащий отрезок  . Отложим от точки . Отложим от точки  на построенном луче равные отрезки: на построенном луче равные отрезки:  , ,   . Соединим точки . Соединим точки  и и  . Проведем через точки . Проведем через точки  , ,  прямые, параллельные* прямой прямые, параллельные* прямой 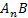 . Они пересекают отрезок . Они пересекают отрезок  в точках в точках 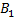 , ,    . Отрезки . Отрезки  , ,   – искомые отрезки. – искомые отрезки.
* см. Билет 45. Билет 14.
 где где 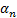 – величина угла правильного n-угольника. Эту величину можно найти по формуле – величина угла правильного n-угольника. Эту величину можно найти по формуле  (следствие из теоремы о сумме углов многоугольника**). Отсюда (следствие из теоремы о сумме углов многоугольника**). Отсюда  . Тогда сторона . Тогда сторона  ; а ; а  . Из . Из последней формулы выразим  . Подставим вместо . Подставим вместо  получившееся выражение: получившееся выражение:  . .
Рассмотрим несколько частных случаев: Для равностороннего треугольника: Для квадрата: Для правильного шестиугольника: ** см. Билет 12. Билет 15. Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки.
Определение: Сумма углов треугольника равна
 и и  равны как накрест лежащие. Аналогично, равны как накрест лежащие. Аналогично,  . Но углы . Но углы  , ,  и и  образуют развернутый угол, следовательно, их сумма равна образуют развернутый угол, следовательно, их сумма равна 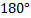 . тогда сумма соответствующих углов треугольника также равна . тогда сумма соответствующих углов треугольника также равна 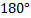 , ч. т. д. , ч. т. д.
Билет 16. Билет 17.
I.
Доказательство: Пусть 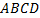 – данный четырехугольник, – данный четырехугольник, 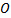 – точка пересечения диагоналей данного параллелограмма. – точка пересечения диагоналей данного параллелограмма. Δ 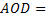 Δ Δ  по первому признаку равенства треугольников ( по первому признаку равенства треугольников ( по условию теоремы, по условию теоремы,  , как вертикальные углы). Следовательно, , как вертикальные углы). Следовательно,  . А они являются внутренними накрест лежащими для прямых . А они являются внутренними накрест лежащими для прямых  и и 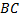 и секущей и секущей  . По признаку параллельности прямых прямые . По признаку параллельности прямых прямые  и и 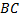 параллельны. Так же доказываем, что параллельны. Так же доказываем, что  и и  тоже параллельны. По определению данный четырехугольник параллелограмм. Теорема доказана. тоже параллельны. По определению данный четырехугольник параллелограмм. Теорема доказана.
II.
Доказательство: Пусть 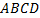 – данный четырехугольник. – данный четырехугольник.  и и  . . Тогда Δ 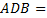 Δ Δ  по первому признаку равенства треугольников ( по первому признаку равенства треугольников ( , как внутренние накрест лежащие между прямыми , как внутренние накрест лежащие между прямыми  и и 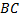 и секущей и секущей  , ,  по условию, по условию,  – общая). – общая). Следовательно,  , а эти углы являются внутренними накрест лежащими для прямых , а эти углы являются внутренними накрест лежащими для прямых  и и  и секущей и секущей  . По теореме признаке параллельности прямых . По теореме признаке параллельности прямых  и и  параллельны. Значит, параллельны. Значит, 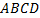 – параллелограмм. Теорема доказана. – параллелограмм. Теорема доказана.
III.
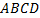 . .  и и  . Проведем диагональ DB. Сумма углов четырех угольника равна сумме углов треугольников . Проведем диагональ DB. Сумма углов четырех угольника равна сумме углов треугольников  и и  . По теореме о сумме углов треугольника, получаем: . По теореме о сумме углов треугольника, получаем: . Так как противолежащие углы в четырехугольнике равны, то . Так как противолежащие углы в четырехугольнике равны, то  и и  . . Углы  и и  являются внутренними односторонними для прямых являются внутренними односторонними для прямых  и и 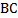 и секущей и секущей  , их сумма равна , их сумма равна 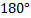 , поэтому из следствия к теореме о признаке параллельности прямых, прямые , поэтому из следствия к теореме о признаке параллельности прямых, прямые  и и 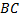 параллельны. Так же доказывается, что параллельны. Так же доказывается, что  . Таким образом, четырехугольник . Таким образом, четырехугольник 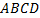 – параллелограмм по определению. Теорема доказана. – параллелограмм по определению. Теорема доказана.
Билет 18. Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.
I.
Доказательство: Пусть 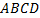 – параллелограмм. Диагональ – параллелограмм. Диагональ  делит его на два треугольника: Δ делит его на два треугольника: Δ  и Δ и Δ  . Эти треугольники равны по стороне и двум углам ( . Эти треугольники равны по стороне и двум углам (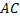 – общая, – общая,  , , 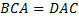 – как накрест лежащие). Отсюда, – как накрест лежащие). Отсюда,  . Теорема доказана. . Теорема доказана.
II. В параллелограмме противоположные углы равны. III.
Доказательство: Пусть 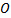 – точка пересечения диагоналей параллелограмма ABCD. Δ – точка пересечения диагоналей параллелограмма ABCD. Δ  Δ Δ  по стороне и двум углам ( по стороне и двум углам ( как вертикал., как вертикал.,  , ,  как накрест лежащие). Отсюда как накрест лежащие). Отсюда  , , 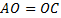 , ч. т. д. , ч. т. д.
Билет 19. Прямоугольником называют параллелограмм, у которого все углы прямые
Доказательство: Рассмотрим прямоугольник 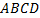 . . Δ  Δ Δ  по двум катетам. Отсюда диагонали по двум катетам. Отсюда диагонали  Обратное утверждение (признак): Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником. Билет 20. Ромбом называется параллелограмм, у которого все стороны равны.
Доказательство: Рассмотрим ромб  , требуется доказать, что , требуется доказать, что 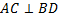 , и что диагонали ромба делят его углы пополам. Докажем, например, что , и что диагонали ромба делят его углы пополам. Докажем, например, что  . Т. к. . Т. к.  , то Δ , то Δ  – равнобедренный. Так как ромб – параллелограмм, то точкой пресечения его диагонали делятся пополам, значит – равнобедренный. Так как ромб – параллелограмм, то точкой пресечения его диагонали делятся пополам, значит 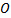 – медиана равнобедренного треугольника – медиана равнобедренного треугольника  , а значит его биссектриса и высота. Поэтому , а значит его биссектриса и высота. Поэтому 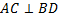 и и  . .
Теорема Менелая
 , , 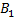 , ,  лежат соответственно на сторонах лежат соответственно на сторонах 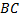 , ,  и и  треугольника Δ треугольника Δ  или на их продолжениях, то они лежат на одной прямой тогда и только тогда, когда или на их продолжениях, то они лежат на одной прямой тогда и только тогда, когда  . .
Доказательство: Проведем через точку Билет 22. Средняя линия треугольника Средняя линия треугольника – отрезок, соединяющий середины двух сторон этого треугольника. Обладает следующими свойствами: 1) Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине. 2) При проведении всех трех средних линий образуются 4 равных треугольника, подобных исходному с коэффициентом 0,5. 3) Средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четверти площади исходного треугольника. Средняя линия трапеции Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Обладает следующими свойствами: 1) средняя линия параллельна основаниям трапеции и равна их полусумме; 2) середины сторон равнобедренной трапеции являются вершинами ромба.
Определение: Доказательство: Расстояние между началом координат и заданной точкой:
Билет 24. Окружностью называется геометрическое место точек, равноудаленных от заданной. Длина окружности: Длина дуги окружности Так как длина окружности равна Билет 25. Билет 26. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Свойства биссектрис треугольника 1) Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла. 2) Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам. 3) Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник. Построение биссектрисы угла Из вершины
Билет 28. Билет 29. Четырехугольник, все вершины которого лежат на окружности, называется вписанным. Билет 30. Вывод формулы Герона
Замечая, что
Билет 33.
Пусть Опустим перпендикуляр Треугольники
Пусть в данном произвольном параллелограмме диагонали равны Билет 34. Трапеция – четырехугольник, у которого только одна пара противолежащих сторон параллельна.
Пусть  Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам...  Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...  Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все...  Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|