|
РАСЧЁТЫ НА ПРОЧНОСТЬ ЗУБЧАТЫХ ПЕРЕДАЧ
Для зубчатых передач ведутся расчёты на прочность по допускаемым напряжениям. Согласно этому методу максимальные напряжения, возникающие в зубчатых колесах при работе, не должны превышать допускаемой величины, свойственной материалу колеса.
При расчёте на контактную выносливость активных поверхностей зубьев, предотвращающую появление питтинга, расчётное контактное напряжение в полюсе зацепления (σH), МПа должно удовлетворять условию
σH ≤ σHP, (5)
где σHP, МПа – допускаемое контактное напряжение.
При расчёте зубьев на выносливость при изгибе расчётное напряжение изгиба зубьев (σF), МПа должно удовлетворять условию
σF ≤ σFP, (6)
где σFP, МПа – допускаемое напряжение изгиба зубьев.
Определение допускаемых контактных напряжений
Допускаемые контактные напряжения определяется раздельно для шестерни и колеса по формуле [6]:
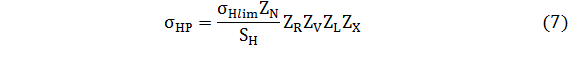
где  – предел контактной выносливости, МПа (табл. 5); – предел контактной выносливости, МПа (табл. 5);  - коэффициент запаса прочности (для зубчатых колес с поверхностным упрочнением - коэффициент запаса прочности (для зубчатых колес с поверхностным упрочнением  =1,2; для колес с однородной структурой (нормализация, улучшение) материала =1,2; для колес с однородной структурой (нормализация, улучшение) материала  =1,1; =1,1; 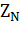 - коэффициент долговечности, определяемый по формулам: - коэффициент долговечности, определяемый по формулам:
 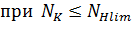 , (8) , (8)
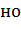 не более 2,6 при SH = 1,1 и не более 1,8 при SH = 1,2. не более 2,6 при SH = 1,1 и не более 1,8 при SH = 1,2.
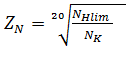 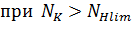 , (9) , (9)
но не менее 0,75.
Здесь 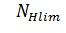 - базовое число циклов напряжений, соответствующее пределу выносливости: - базовое число циклов напряжений, соответствующее пределу выносливости:
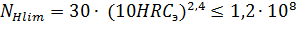 циклов; (10) циклов; (10)
 - число циклов напряжений в соответствии с заданным сроком службы: - число циклов напряжений в соответствии с заданным сроком службы:
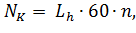 (11) (11)
 где где 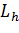 - срок службы в часах; n – частота вращения колеса, для материала которого определяют допускаемые напряжения, мин-1. - срок службы в часах; n – частота вращения колеса, для материала которого определяют допускаемые напряжения, мин-1.
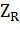 – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев; – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев; 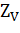 – коэффициент, учитывающий окружную скорость; – коэффициент, учитывающий окружную скорость; 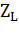 – коэффициент, учитывающий влияние смазки; – коэффициент, учитывающий влияние смазки; 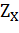 - коэффициент, учитывающий размер зубчатого колеса. Для проектировочного расчета можно принять - коэффициент, учитывающий размер зубчатого колеса. Для проектировочного расчета можно принять 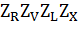 = 0,9 [6]. = 0,9 [6].
Таблица 5. Расчетные формулы для определения предела
контактной выносливости
| Способ термической обработки
| Средняя твердость поверхности зубьев
| Сталь
| Формула для расчета значений  , МПа , МПа
| | Нормализация или улучшение
| менее 350 НВ
|
углеродистая и легированная
| 
| | Объемная или поверхностная закалка
| 38 …50 HRCэ
|  = 17 = 17  + 200 + 200
| | Цементация или нитроцементация
| более 56 HRCэ
|
легированная
|  = 23 = 23 
| | Азотирование
| более 550 НВ
|  = 1050 = 1050
| Таблица 6. Результаты расчета допускаемых контактных напряжений
| Объект расчета
| Сталь
| Средняя твердость
| 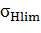 , МПа (табл. 5) , МПа (табл. 5)
| 
|  циклов
ф-ла (11) циклов
ф-ла (11)
|  циклов
ф-ла (10)
циклов
ф-ла (10)
| 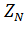
|  МПа
ф-ла (7)
МПа
ф-ла (7)
| | Шестерня 1 ступени
| 40ХН
| 50,5
| 1058,5
| 1,2
| 10,48.108
| 0,98.108
| 0,89
| 706,5
| | Колесо 1 ступени
| 40Х
| 47,5
| 1007,5
| 1,2
| 1,47.108
| 0,8.108
| 0,97
|
| | Шестерня 2 ступени
| 40ХН
| 50,5
| 1058,5
| 1,2
| 1,47.108
| 0,98.108
| 0,98
|
| | Колесо 2 ступени
| 40Х
| 47,5
| 1007,5
| 1,2
| 0,4.108
| 0,8.108
| 1,12
|
| В результате расчета принимаем:
для I-ой ступени  = 706,5 МПа, = 706,5 МПа,
для II-ой ступени  = 778 МПа. = 778 МПа.
Определение допускаемых напряжений при изгибе зуба
Допускаемые напряжения при изгибе зуба 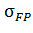 определяют для шестерни и колеса по формуле [6]: определяют для шестерни и колеса по формуле [6]:
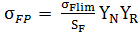 , (12) , (12)
где 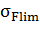 - предел выносливости зубьев при изгибе, определяемый по таблице 8; - предел выносливости зубьев при изгибе, определяемый по таблице 8; 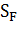 - коэффициент запаса прочности, значения которого для вероятности неразрушения 0,99 принимают - коэффициент запаса прочности, значения которого для вероятности неразрушения 0,99 принимают 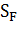 = 1,55…1,7 (табл. 7); = 1,55…1,7 (табл. 7);
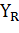 – коэффициент, учитывающий шероховатость переходной поверхности зуба. При шероховатости не более R а = 1,6 мкм, – коэффициент, учитывающий шероховатость переходной поверхности зуба. При шероховатости не более R а = 1,6 мкм, 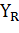 = 1; = 1;
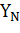 - коэффициент долговечности для зубчатых колес с однородной структурой и для зубчатых колес, закаленных при нагреве ТВЧ, определяется по формуле: - коэффициент долговечности для зубчатых колес с однородной структурой и для зубчатых колес, закаленных при нагреве ТВЧ, определяется по формуле:
 , (13) , (13)
где 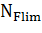 - базовое число циклов нагружения ( - базовое число циклов нагружения (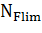 =4 . 106). =4 . 106).
Если 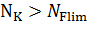 , следует принять , следует принять 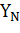 = 1. Результаты вычисления = 1. Результаты вычисления 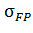 по формуле (12) приведены в таблице 8. по формуле (12) приведены в таблице 8.
Таблица 7. Расчетные формулы для определения предела
выносливости зубьев при изгибе [6]
| Марка стали
| Способ термической обработки
| Твердость зубьев
| 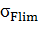 , МПа , МПа
| Коэффициент запаса прочности 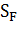
| | Углеродистая и легированная марок 45, 40ХН, 45Х
| Нормализация или улучшение
| 180…350НВ
| 1,75HНВ
| 1,7
| | Легированная марок 40Х, 45Х, 40ХН
| Объемная
закалка
| 45…55 HRCэ
|
| 1,7
| | Цементуемая сталь 18ХГТ, 20Х, 20ХГТ
| Цементация и закалка
| 57…63 HRCэ
|
| 1,55
|
Таблица 8. Результаты расчета допускаемых напряжений при изгибе
| Объект расчета
| Сталь
| Средняя твердость НВ
| 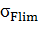 , МПа , МПа
| Коэффициенты
| 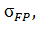 МПа
МПа
| 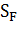
| 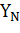
| 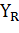
| | Шестерня 1 ступени
| 40ХН
| 285,5
|
| 1,7
|
|
|
| | Колесо 1 ступени
| 40Х
| 285,5
|
| 1,7
|
|
|
| | Шестерня 2 ступени
| 40ХН
| 285,5
|
| 1,7
|
|
|
| | Колесо 2 ступени
| 40Х
| 285,5
|
| 1,7
|
|
|
|
ПРОЕКТИРОВОЧНЫЙ РАСЧЕТ ЗАКРЫТОЙ
ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ
Ориентировочное значение межосевого расстояния aw (мм) из условия контактной выносливости определяют по формуле [3]:
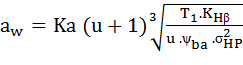 , (14) , (14)
где 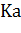 – вспомогательный коэффициент. Для прямозубых передач – вспомогательный коэффициент. Для прямозубых передач 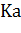 = 495, для косозубых передач = 495, для косозубых передач 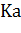 = 430; = 430; 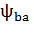 = b2/ = b2/ 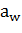 – коэффициент ширины венца b2 колеса, равный 0,4…0,5 при симметричном расположении и 0,25…0,4 – при несимметричном расположении колес относительно опор (индекс 1 у параметров относится к ведущему зубчатому колесу (шестерне), индекс 2 – к ведомому); u – передаточное число ступени передачи; Т1 – крутящий момент на ведущем валу, Н.м; – коэффициент ширины венца b2 колеса, равный 0,4…0,5 при симметричном расположении и 0,25…0,4 – при несимметричном расположении колес относительно опор (индекс 1 у параметров относится к ведущему зубчатому колесу (шестерне), индекс 2 – к ведомому); u – передаточное число ступени передачи; Т1 – крутящий момент на ведущем валу, Н.м; 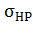 - допускаемое контактное напряжение колеса с менее прочным зубом, МПа; - допускаемое контактное напряжение колеса с менее прочным зубом, МПа; 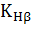 – коэффициент неравномерности нагрузки по длине зуба. Его значения находятся в таблице 9. Величина этого коэффициента зависит от характера расположения зубчатых колес в редукторе и от ширины венца b колеса. Эта ширина выражается коэффициентом ψbd = b/d, где d – делительный диаметр зубчатого колеса. Соотношение между коэффициентами – коэффициент неравномерности нагрузки по длине зуба. Его значения находятся в таблице 9. Величина этого коэффициента зависит от характера расположения зубчатых колес в редукторе и от ширины венца b колеса. Эта ширина выражается коэффициентом ψbd = b/d, где d – делительный диаметр зубчатого колеса. Соотношение между коэффициентами 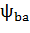 и ψbd выражается следующим образом [7]: и ψbd выражается следующим образом [7]:
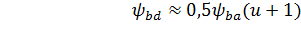 . (15) . (15)
Для определения коэффициента 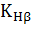 следует установить значение коэффициента следует установить значение коэффициента 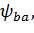 затем по формуле (15) рассчитать затем по формуле (15) рассчитать 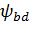 и по таблице 9 получить искомую величину. и по таблице 9 получить искомую величину.
Для первой (быстроходной) ступени рекомендуется принять  = 0,25; для второй – 0,315. Тогда для быстроходной ступени = 0,25; для второй – 0,315. Тогда для быстроходной ступени 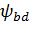 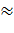 1.01, а для тихоходной ступени – 1.01, а для тихоходной ступени – 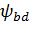 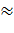 0,72. Для низкой твёрдости зубьев быстроходной ступени 0,72. Для низкой твёрдости зубьев быстроходной ступени 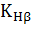 = 1,15, а при высокой твёрдости зубьев – = 1,15, а при высокой твёрдости зубьев – 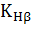 = 1,4. Аналогично для тихоходной передачи схемы 1 этот коэффициент примет соответственно значения = 1,4. Аналогично для тихоходной передачи схемы 1 этот коэффициент примет соответственно значения 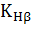 = 1,05 и = 1,05 и 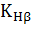 = 1,13. = 1,13.
Таблица 9. Значения коэффициента 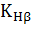
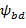
| Твёрдость зубьев H1≤350HB, H2≤350HB
| Твёрдость зубьев H1>350HB, H2>350HB
| | БП
| ТП схем 1 и 2
| ТП схемы 3
| БП
| ТП схем 1 и 2
| ТП схемы 3
| | 0,2
| 1,03
| 1,01
|
| 1,06
| 1,02
|
| | 0,4
| 1,05
| 1,02
|
| 1,13
| 1,05
| 1,01
| | 0,6
| 1,08
| 1,04
| 1,01
| 1,2
| 1,1
| 1,02
| | 0,8
| 1,12
| 1,06
| 1,02
| 1,3
| 1,15
| 1,04
| | 1,0
| 1,15
| 1,08
| 1,03
| 1,4
| 1,2
| 1,06
| | 1,2
| 1,2
| 1,1
| 1,04
| 1,5
| 1,25
| 1,09
| | 1,4
| 1,25
| 1,13
| 1,05
| –
| 1,32
| 1,13
| | 1,6
| 1,3
| 1,15
| 1,07
| –
| –
| –
| Примечание. БП – быстроходная передача для всех схем, ТП – тихоходная передача для указанных схем. Значение коэффициента 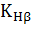 для промежуточных значений коэффициента для промежуточных значений коэффициента 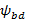 определяется интерполяцией. определяется интерполяцией.
Для косозубой (быстроходной) передачи допускаемое напряжение может быть повышено до значения:
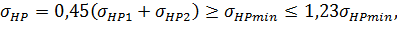 (16) (16)
где 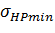 – меньшее значение из двух величин: – меньшее значение из двух величин:  . .
Расчётное значение межосевого расстояния следует округлять до ближайшего стандартного значения из ряда размеров [8]:
40, 50, 60, 71, 80, 90, 100, 112, 125, 140, 160, 180, 200, 224, 250.
Ориентировочное значение модуля m, мм определяется из условия выносливости зубьев при изгибе для принятого межосевого расстояния aw по формуле [6]:
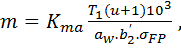 (17) (17)
где  = 6,8 – вспомогательный коэффициент для прямозубых передач, = 6,8 – вспомогательный коэффициент для прямозубых передач,  = 5,8 – для косозубых передач; b´2 – предварительная ширина венца колеса = 5,8 – для косозубых передач; b´2 – предварительная ширина венца колеса 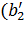 = =  . aw), мм; . aw), мм; 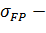 допускаемое напряжение при изгибе зуба менее прочного колеса. допускаемое напряжение при изгибе зуба менее прочного колеса.
Полученное значение модуля m округляется в большую сторону до стандартного значения из любого ряда чисел:
1 ряд: 1,25; 1,5; 2; 2,5;3; 4; 5; 6; 8.
2 ряд: 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7.
В силовых зубчатых передачах при твердости зубьев колес 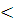 350 НВ рекомендуется принимать модуль m 350 НВ рекомендуется принимать модуль m 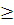 1,25 мм, при твердости одного из колес более 45 HRCэ – m 1,25 мм, при твердости одного из колес более 45 HRCэ – m 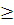 1,5 мм. 1,5 мм.
Таблица 10. Результаты расчета межосевых расстояний aw и модулей m для первой и второй передач (ступеней) редуктора
| Объект расчета
| T1
H.м (табл. 3)
| u
стр.11
| Ψba
| Ψbd
| KHβ
| σНP, МПа (табл.6)
| aw, расч.мм (14)
| aw, принятое, мм
| b'2, мм
| σFP, МПа (табл.8)
| m расч.мм (17)
| m принятое, мм
| | Косозубая передача 1 ступени
| 47,8
| 7,1
| 0,25
| 1,01
| 1,4
| 706,5
|
|
|
|
| 1,51
| 2,0
| | Прямозубая передача 2 ступени
| 325,9
| 3,55
| 0,315
| 0,72
| 1,1
|
|
|
|
|
| 3,22
| 3,5
| Примечание. Ширина венца определена по формуле 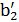 = =  . aw с учётом коэффициента . aw с учётом коэффициента  , принимающего значения для первой ступени – 0,25; для второй – 0,315. , принимающего значения для первой ступени – 0,25; для второй – 0,315.
Минимальное значение угла наклона зуба для косозубой передачи 1 ступени определяется по формуле:
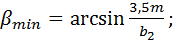 (18) (18)
Не рекомендуется выбирать максимальное значение более 22°, для шевронных – 30°…40°. Выбрав угол β, определяем суммарное число зубьев колеса и шестерни по формуле:
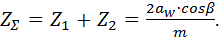 (19) (19)
Принимаем ближайшее целое число. Уточним действительную величину угла наклона зубьев первой ступени:
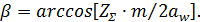 (20) (20)
Определим число зубьев (для первой и второй ступеней):
 (21) (21)
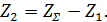 (22) (22)
Для того, чтобы не допустить подрезки зуба при нарезании червячной фрезой без специального корригирования, минимальное число зубьев шестерни не должно быть меньше 17, т.е.  Если расчётное число окажется меньше 17, то следует принять 17, изменив число зубьев колеса Если расчётное число окажется меньше 17, то следует принять 17, изменив число зубьев колеса 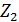 в соответствии с формулой (22). Так следует сделать, чтобы не изменять межосевого расстояния (обычно, это относится к первой ступени). При этом изменится передаточное число первой ступени. Для того, чтобы сохранить передаточное число редуктора, следует соответственно изменить передаточное число второй ступени. в соответствии с формулой (22). Так следует сделать, чтобы не изменять межосевого расстояния (обычно, это относится к первой ступени). При этом изменится передаточное число первой ступени. Для того, чтобы сохранить передаточное число редуктора, следует соответственно изменить передаточное число второй ступени.
Определение фактического передаточного числа любой ступени производится по формуле:
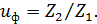 (23) (23)
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




