Тема 10. Индексный метод в статистических исследованиях.
Цель занятия: понять, что такое индексы и показать какие задачи решают при помощи индексов. Рассмотреть индивидуальные индексы, сводные индексы в агрегатной форме, индексы в средней арифметической и средней гармонической формах, индексы переменного, фиксированного состава и структурных сдвигов.
Контрольные вопросы.
1. Что называется индексом в статистике?
2. Что характеризуют индивидуальные индексы. Приведите примеры.
3. В чем сущность общих индексов?
4. Для чего необходимо деление на индексы объемных (количественных) и качественных показателей и какая система взвешивания принята в теории индексов?
5. Как исчисляется агрегатный индекс стоимости продукции (товарооборота в фактических ценах) и что он характеризует?
6. Как исчисляется агрегатный индекс физического объема продукции (товарооборота) и что он характеризует?
7. Когда возникает необходимость преобразования индекса физического объема в средний арифметический и средний гармонический?
8. Как исчисляют агрегатные индексы цен, себестоимости, производительности труда и что они показывают?
9. Что называется индексом переменного состава, как он исчисляется и что характеризует?
10. Какой индекс называется индексом фиксированного состава, как он исчисляется и что характеризует?
11. Что характеризует индекс структурных сдвигов и как он исчисляется?
12. Какая взаимосвязь существует между индексами переменного, фиксированного составов и структурных сдвигов?
13. Что представляет собой система взаимосвязанных индексов?
Задания для практических работ.
Задача №1. Имеются следующие данные о реализации плодово-ягодной продукции в области:
| Наименование товара
| Июль
| Август
| | Цена за 1 кг., руб.
| Продано, т.
| Цена за 1 кг., руб.
| Продано, т.
| | Черешня
|
|
|
|
| | Персики
|
|
|
|
| | Виноград
|
|
|
|
| Требуется рассчитать: 1. Индекс товарооборота.
2. Сводный индекс цен.
3. Индекс физического объема реализации.
Задача №2. Имеются данные службы еженедельного наблюдения цен о продаже товаров в районе:
| Товар
| Продано
21 марта, млн. руб.
| Изменение цен
с 14 по 1 марта, %
| | Туфли мужские, пары.
|
|
| | Костюмы спортивные, шт.
|
|
|
Требуется определить средний гармонический индекс цен.
Задача №3. Имеются следующие данные о выпуске продукции мебельной фабрики:
| Наименование изделия
| Изменение выпуска продукции в мае по сравнению с апрелем, %
| Выпуск продукции в апреле, млн. руб.
| | Столы
|
|
| | Диваны
|
|
| | Стулья
|
|
|
Определить увеличение выпуска всей продукции в мае по сравнению с апрелем, т.е. рассчитать общий индекс физического объема.
Задача №4. Имеем трудоемкость и выпуск изделий А, Б и В на предприятии:
| Вид продукции
| Затраты времени на 1 изд., чел – час.
| Произведено, шт.
| | январь
| февраль
| январь
| февраль
| | Изд. А
| 1,0
| 0,9
|
|
| | Изд. Б
| 1,2
| 1,0
|
|
| | Изд. В
| 0,9
| 0,8
|
|
|
Рассчитать сводный индекс производительности труда по трудоемкости.
Задача №5. Имеются следующие данные о производстве продукции и отпускных ценах предприятия:
| Вид продукции
| Сентябрь
| Октябрь
| Отпускная цена, руб.
| | Произведено, шт.
| Трудовые затраты, чел – час.
| Произведено, шт.
| Трудовые затраты, чел – час.
| | Изд. А
|
|
|
|
|
| | Изд. Б
|
|
|
|
|
| | Изд. В
|
|
|
|
|
|
Вычислить индекс производительности труда в стоимостном выражении.
Литература по теме:
Основная:
1. Гусаров В.М. Статистика: Учебное пособие для ВУЗов. – М.: ЮНИТИ – ДАНА, 2002. Гл.8, п.п. 8.1; 8.2; 8.3; 8.4; 8.5; 8.6 (с. 143-178).
2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. – М.: ИНФРА – М, 2000. Гл. 9, п.п. 9.1; 9.2; 9.3; 9.4; 9.5 (с. 339-390).
3. Практикум по теории статистики. Под ред. проф. Шмойловой Р.А. – М.: Финансы и статистика, 2002. Гл.12, п.п. 12.1 (с. 229-309).
Дополнительная:
1.Годин А.М. Статистика: Учебник. – М.: Издательско-торговая корпорация. «Дашков и Ко», 2002. Гл. X, параграф 1,2,3,4,5,6,7,8,9,10,11 (с. 250-284).
2. Сиденко А.В., Попов Г.Ю., Матвеева В.М. Статистика: Учебник. – М.: «Дело и сервис», 2000. Гл.11, п.п. 11.1; 11.2; 11.3; 11.4; 11.5; 11.6; 11.7 (с. 93-111).
3. Статистика. Учебник /Под редакцией проф. Н.Н. Елисеевой – М.: ООО «ВИТРЭМ», 2002. Гл.9, п.п. 9.1; 9.2; 9.3 (с. 217-230).
4. Томас Р. Количественные методы анализа хозяйственной деятельности /Пер. с англ./ М.: «Дело и сервис», 1999. Гл.5, п.п. 5.1; 5.2; 5.3; 5.4; 5.5; 5.6; 5.7; 5.8; 5.9; 5.10; 5.11; 5.12; 5.13; 5.14; 5.15 (с. 157-180).
5. Статистика: Курс лекций /Харченко Л.П., Долженкова В.Г., Ионин В.Г. и ор.; Под ред. к.э.н. В.Г. Ионина – Новосибирск: изд-во НГАЭ и У, М.: ИНФРА – М, 1999. Гл.6, п.п. 6.1; 6.2; 6.3; 6.4; 6.5; 6.6; 6.7 (с. 111-127).
Примечание инновационной технологии – примеры тестовых заданий по курсу дисциплины (на последнем практическом занятии).
Тестирование (выберите один варианта ответа)
Задание №1. предметом изучения статистики являются статистические…
1. Совокупности
2. Показатели
3. Единицы
4. Таблицы
Задание №2. что представляет собой статистическая методология…
1. Социально-экономическая теория.
2. Принцип диалектического материализма.
3. Совокупность общих правил (принципов), специальных приемов и методов статистического исследования.
4. Понимание сущности изучаемого объекта или процесса.
Задание №3. Одной из основных задач статистики…
1. Информация о конкретной фирме.
2. Обеспечение полноты и достоверности учета хозяйственных субъектов и их характеристику.
3. Всестороннее освещение социально-экономического положения РФ, происходящих изменений.
4. Публикации статистической информации.
Задание №4. Задачей статистического наблюдения являются…
1. Первичная обработка и сводка данных.
2. Сбор массовых данных об изучаемых явлениях (процессах).
3. Расчет обобщающих показателей.
4. Выявление количественных закономерностей.
Задание №5. Исследование взаимосвязей варьирующих признаков в пределах однородной совокупности называется … группировкой.
1. Типологической.
2. Структурной.
3. Множественной.
4. Аналитической.
Задание №6. Графическое изображение статистических данных используемые для характеристики структуры социальных явлений называется…
1. Линейные диаграммы.
2. Столбиковые диаграммы.
3. Полосовые диаграммы.
4. Секторные диаграммы.
Задание №7. Относительная величина сравнения характеризует…
1. Соотношение фактического и планового уровня показателя.
2. Соотношение плановой величины показателя и величины, предшествующей планируемому периоду.
3. Соотношение одних и тех же показателей двух разных объектов, групп, совокупностей.
4. Соотношение показателя, характеризующего часть совокупности и показателя по всей совокупности в целом.
Задание №8. Как называются показатели, которые получают непосредственно в процессе статистического наблюдения…
1. Относительные показатели.
2. Абсолютные показатели.
3. Совокупность взаимосвязанных показателей.
4. Средние величины.
Задание №9. Как называется средняя величина, когда отдельные значения осредняемого признака могут повторятся…
1. Средняя гармоническая простая.
2. Средняя кубическая простая.
3. Средняя квадратическая простая.
4. Средняя арифметическая взвешенная.
Задание №10. Если значение всех признаков (Хi) увеличить в два раза, то чему будет равно среднее значение признаков…
1. Среднее значение признака остается неизменной.
2. Среднее значение признака уменьшиться в два раза.
3. Среднее значение признака увеличивается в два раза.
4. Среднее значение признака увеличивается в четыре раза.
Задание №11. При увеличении всех значений признака (Xi) на 4 единицы, то чему будет равно среднее значение признака…
1. Среднее значение признака уменьшится на 2 единицы.
2. Среднее значение признака увеличивается на 2 единицы.
3. Среднее значение признака уменьшится на 3 единицы.
4. Среднее значение признака увеличивается на 4 единицы.
Задание №12. Если вес (частота) уменьшится в два раза, то чему будет равно среднее значение признака…
1. Среднее значение признака увеличивается в два раза.
2. Среднее значение признака увеличивается в четыре раза.
3. Среднее значение признака уменьшится в два раза.
4. Среднее значение признака не изменится.
Задание №13. Если имеются данные о значении дисперсии, то какое можно рассчитать значение…
1. Размаха вариации.
2. Среднего линейного отклонения.
3. Коэффициента вариации.
4. Среднего квадратического отклонения.
Задание №14. К абсолютным показателям вариации относятся…
1. Коэффициент осцилляции
2. Коэффициент вариации.
3. Относительное линейное отклонение.
4. Размах вариации.
Задание №15. Если все значение признака (Хi) уменьшить на величину в 2 единицы, то, что произойдет с дисперсией…
1. Дисперсия уменьшится на величину в 2 единицы.
2. Дисперсия увеличится на величину в 2 единицы.
3. Дисперсия не изменится.
4. Дисперсия увеличится в два раза.
Задание №16. Если все значения признака (Хi) увеличить в два раза, то, что произойдет с дисперсией…
1. Дисперсия увеличится в два раза.
2. Дисперсия увеличится в четыре раза.
3. Дисперсия не изменится.
4. Дисперсия уменьшится в два раза.
Задание №17. Связи в статистике по аналитическому выражению классифицируются на …
1. Прямые и обратные.
2. Закономерные и произвольные.
3. Сильные и слабые.
4. Линейные и криволинейные.
Задание №18. Как называют связь, при которой определенному значению факторного признака (Х) соответствует одно значение результативного признака (У)…
1. Стохастическую связь.
2. Корреляционную связь.
3. Функциональную связь.
4. Ранговые коэффициенты связи.
Задание №19. Для изучения функциональных связей применяются методы…
1. Метод аналитических группировок.
2. Непараметрические методы.
3. Корреляционно-регрессионный анализ.
4. Балансовый и индексный метод.
Задание №20. По какой формуле определяется коэффициент корреляции рангов Кендела:
1.  ; ;
2.  ; ;
3.  ; ;
4. 
Задание №21. Как называется метод, позволяющий измерить интенсивность связи, как между количественными признаками, так и между качественными признаками, которые поддаются ранжированию…
1. Линейный коэффициент корреляции.
2. Коэффициент корреляции знаков по Г. Фехнеру.
3. Коэффициент корреляции рангов Спирмена.
4. Коэффициент ассоциации и контингенции.
Задание №22. По какой формуле определяется средний уровень ряда для моментного динамического ряда с неравноотстоящими уровнями:
1.  ; ;
2.  ; ;
3.  ; ;
4. 
Задание №23. Если примерно постоянными оказываются темпы роста динамического ряда, то для выравнивания применяется…
1. Простая экспонента.
2. Показательная функция.
3. Логитическая кривая.
4. Линейная функция.
Задание №24. Как называются ряды распределения, построенные по качественным признакам…
1. Вариационные.
2. Комбинированные.
3. Атрибутивные.
4. Интервальные.
Задание №25. Укажите формулу агрегатного индекса физического объема продукции…
1.  ; ;
2. 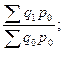 
3.  ; ;
4. 
Задание №26. Взаимосвязь индексов. Укажите формулу индекса изменения объема продукции…
1. Ip*Iq
2. IZ*Iq
3. IT*IW
4. IT* IЗар. пл.
Задание №27. Если объем случайной повторной выборки увеличить в 4 раза, то какая будет ее средняя ошибка…
1. Увеличится в 4 раза.
2. Уменьшится в 4 раза
3. Уменьшится в 2 раза.
4. Не изменится.
Задание №28. Как называется вид выборки по способу отбора единиц из генеральной совокупности, производится наугад или наудачу без каких-либо элементов системности…
1. Механическая выборка.
2. Собственно-случайная выборка.
3. Серийная выборка.
4. Комбинированная выборка.
6. Задание для самостоятельной работы студентов.
| № п\п
| Темы для самостоятельного изучения
| Виды и содержание для самостоятельной работы
| |
|
|
| |
3.
4.
| Сведения из истории статистики. Структура статистической науки. Современная организация статистики в РФ и ее задачи.
Контрольные вопросы по темам 1,2,3:
- Что означает термин «статистика»?
- Что является предметом исследования статистической науки.
- В чем заключается сущность статистической методологии?
- Какие конкретные виды статистического наблюдения используются для сбора данных?
- Поставьте цель, определите объект, единицу наблюдения, конкретные признаки. Составьте программу статистического наблюдения.
- Для чего и кому нужна статистическая информация в современных условиях?
-С какой целью строятся графики в экономико – статистических исследованиях?
- В каких целях используются диаграммы (секторные, столбиковые и др.)?
Задания для практических работ
Задача №1. Имеем данные отражающие дневную выработку 4 предприятий:
| Предприятие
| А
| Б
| В
| Г
| | Дневная выработка, изд.
|
|
|
|
|
Выполнить графическое изображение столбиковой диаграммой.
Задача №2. Имеем стоимостное выражение экспорта ряда стран за определенный месяц:
| Страна
| США
| Канада
| Англия
| Франция
| Германия
| | Экспорт, млн. долл.
|
|
|
|
|
|
Построить полосовую диаграмму.
Задача №3. Имеем годовые затраты отделов предприятий, связанные с определенной группой товаров:
| Отдел
| Производственный
| Сбыта
| Маркетинга
| Исследовательский
| Материально-техническое обеспечение
| | Расходы, тыс. руб
|
|
|
|
|
|
Построить секторную диаграмму.
Контрольные вопросы по теме 4:
- Достаточно ли одних абсолютных показателей для анализа изучаемого явления?
- Каковы основные условия правильного расчета относительного показателя?
- В какой форме могут быть выражены относительные показатели.
Задания для практических работ.
Задача №1. Продажа продовольственных товаров в магазине:
| Годы
|
|
|
|
|
| | Продажа продовольственных товаров, тыс. руб.
|
|
|
|
|
|
Вычислить относительные показатели динамики с постоянной и переменной базой. Сделайте выводы.
Задача №2. Планом предприятия на 2006 г. по сравнению с 2005 г. было предусмотрено снижение себестоимости на 8 %. Фактическое снижение на 6 %. Вычислите относительную величину выполнения плана по снижению себестоимости продукции в 2006 г.
Задача №3. Розничный товарооборот магазина за 2007. составил 1800 тыс. руб., в том числе непродовольственных товаров – 950 тыс. руб., продовольственных товаров – 850 тыс. руб. Определить структуру товарооборота магазина.
Контрольные вопросы по теме 5:
- Роль средних величин в регулировании действия случайных причин.
- В чем смысл научно – обоснованного использования средних величин?
- Как исчисляется средняя арифметическая из интервального вариационного ряда?
В каких случаях применяется простая и взвешенная гармоническая средняя?
| Проработка учебного материала. Решение задач. Умение делать выводы.
Проработка учебного материала. Решение задач. Умение делать выводы.
| |
5.
6.
7.
| Задания для практических работ
Задача №1. Требуется рассчитать среднюю часовую выработку одного рабочего по следующим данным:
| Рабочие
| Произведено изд. за неделю, шт.
| Часовая выработка
| |
|
|
| |
|
|
| |
|
|
|
Задача №2. Три предприятия заняты производством соковарных аппаратов одной и той же конструкции. Себестоимость производства на первом предприятии 5 тыс. руб., на втором – 4 тыс. руб., а на третьем 6 тыс. руб. Определить среднюю себестоимость соковарного аппарата при условии, что на каждом предприятии общие затраты на его изготовление составляют 68 тыс. руб.
Задача №3. Имеются следующие данные о распределении рабочих по затратам времени на обработку одного кулинарного изделия:
| Затраты времени на одну обработку изд., мин.
| Число рабочих, чел.
| | 4,5 – 5,5
|
| | 5,5 – 6,5
|
| | 6,5 – 7,5
|
| | 7,5 – 8,5
|
| | 8,5 – 9,5
|
| | 9,5 – 10,5
|
| | 10,5 – 11,5
|
|
Требуется определить:
- Среднюю величину времени на обработку одного кулинарного изделия.
- Моду и медиану.
Контрольные вопросы по теме 6:
- Что представляет собой дисперсия альтернативного признака?
- Основные свойства дисперсии.
- Значение коэффициента вариации для экономического анализа.
- Какая вариация называется систематической, случайной?
- Что представляет собой правило сложения дисперсии?
Задания для практических работ.
Задача №1. В трех партиях продукции было обнаружено:
- первая партия – 1300 изд., из них 980 годных. 320 бракованных;
- вторая партия – 730 изд., из них 700 годных. 30 бракованных;
- третья партия - 890 изд., из них 840 годных. 50 бракованных;
Требуется определить в целом для всех партий следующие показатели:
- Средний процент годной продукции и средний процент брака.
- Дисперсию, средние квадратическое отклонение и коэффициент вариации годной продукции.
Задача №2. Численность и удельный вес одной из категорий крупного рогатого скота фермерских хозяйств района, см. таблицу:
| Хозяйство
| Удельный вес дойных коров, %
| Всего коров
| |
|
|
| |
|
|
| |
|
|
|
Требуется определить:
- Долю дойных коров в целом по 3-м хозяйствам.
- Общую дисперсию доли дойных коров.
- Внутригрупповую дисперсию.
- Среднюю из внутригрупповых дисперсий.
- Межгрупповую дисперсию.
- Проверить правило сложения дисперсий
Задача №3. имеются выборочные данные о стаже работников фирмы:
| Стаж работы, лет
| До 4
| 4-6
| 6-8
| 8-10
| Св. 10
| | Среднесписочная численность работников, чел.
|
|
|
|
|
|
Требуется определить:
- Средний стаж работников фирмы,
- Дисперсию.
- Среднее квадратическое отклонение.
- Среднее линейное отклонение.
- Коэффициент вариации.
Контрольные вопросы по теме 7:
- Вопросы, которые нужно решать для проведения выборочного наблюдения?
- Смысл коэффициента доверия.
- Как исчисляется средние и предельные статистические ошибки выборки?
- Что такое метод отбора и способ отбора единиц из генеральной совокупности?
Задания для практических работ
Задача №1. В банке с численностью 350 человек в январе 2007 года была произведена 20%-ная механическая выборка. По результатам наблюдения оказалось, что у 10% обследованных потери времени достигли более 40 мин. в день. С вероятностью 0,683 установите пределы, в которых находятся генеральная доля служащих с потерями рабочего времени более 40 мин. в день.
Задача №2. Сколько рабочих фирмы нужно обследовать в порядке случайной выборки для определения средней заработной платы, чтобы с вероятностью равной 0,945 можно было гарантировать предельную ошибку не более 5 руб. Предполагаемое среднее квадратическое отклонение равно 20 руб.
Задача №3. Для определения доли сотрудников коммерческих банков области в возрасте старше 50 лет предполагается организовать типическую выборку пропорционально численности сотрудников мужского и женского пола с механическим отбором выборки групп. Общее число сотрудников банков 20 тыс.чел., в том числе 13 тыс. мужчин и 7 тыс. женщин. На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 2050. Определите необходимый объем выборки при вероятности 0,954 и ошибке 8%.
Контрольные вопросы по теме 8:
- Определение статистической модели?
- Основные проблемы и правила построения однофакторной линейной регрессионной модели.
- Правила построения многофакторной корреляционной модели.
- Значимость коэффициента регрессии.
- Экономический смысл коэффициента эластичности.
Задания для практических работ
Задача №1. По пяти предприятиям имеем данные цены товара и дальности его перевозки:
| Номер предприятия
| Дальность перевозки, км
| Цена товара, руб.
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| Требуются определить:
- Тесноту связи между показателями по линейному коэффициенту корреляции.
- Коэффициент детерминации.
Задача №2. Выборочные данные по 10 однородным предприятиям:
| Номер предприятия
| Энерговооруженность труда на одного рабочего, кВт/ч
| Выпуск продукции на одного рабочего, Т.
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| Построить однофакторную регрессионную модель.
|
Проработка учебного материала. Решение задач. Умение делать выводы.
Проработка учебного материала. Решение задач. Умение делать выводы.
Проработка учебного материала. Решение задач. Умение делать выводы.
| | 8.
9.
| Контрольные вопросы по теме 9:
- Задачи динамики явлений.
- Важнейшее условие правильного построения динамического ряда.
- Причины возникновения несопоставимости динамических рядов.
- Что такое средний абсолютный прирост?
- Какими статистическими методами осуществляется изучение тренда в рядах динамики?
Задания для практических работ
Задача №1. Стоимость набора из 25 основных продуктов питания в расчете на месяц на одного человека в I квартале 2006 г. характеризуется следующими темпами прироста стоимости к предыдущему месяцу, %:
Январь Февраль Март
+6,3 +3,6 +2,9
Определить: 1. Базисные темпы роста стоимости продуктового набора в марте к декабрю 2005 г.
2.Среднемясечный темп прироста стоимости продуктового набора с января по март.
Задача №2. Темп прироста (снижения) производства отрасли (в сопоставимых ценах) характеризуется показателями, %:
| 2002г
| 2003г
| 2004г
| 2005г
| 2006г
| | +5
| +4
| -12
| -18
| -30
| Определить: 1. Цепные (годовые) темпы роста и прироста.
2. Среднегодовые темпы роста и прироста с 2002 по 2006гг.
Задача №3. Данные об остатках средств на расчетном счете фирмы:
- на 01.01. остаток средств составил 170 тыс.руб.
- на 10.01. поступило от покупателей 275 тыс.руб.
- на 15.01. списано со счетов на хозяйственные нужды 27 тыс.руб.
- на 18.01. снято со счета для выплаты заработных плат 195 тыс.руб.
- на 25.01. поступило от покупателей 530 тыс. руб.
Других изменений до конца месяца не было. Требуется определить средний остаток средств на расчетном счете в январе.
Задача №4. Объем сделок по продуктам составил:
- 10.02.07 – 80 млн.руб.
- 15.02.07 – 110 млн.руб.
Требуется определить прогноз сделок на 16.02. 07 года по среднему абсолютному прироста ( ). ).
Контрольные вопросы по теме 10:
- Задачи решаемые при помощи индексов?
- В каком случае возникает необходимость преобразования агрегатного индекса цен в средний гармонический и средней арифметической?
- Принципы построения базисных и цепных индексов и какая существует между ними взаимосвязь?
- Что представляет собой индексы с фиксированными и переменными весами?
- Как практически используется взаимосвязь индексов цен, физического объема и товарооборота?
Задания для практических работ
Задача №1. Имеются данные о продаже товаров на рынке:
| Товары
| Количество проданных товаров, тыс.
| Цена за единицу товара, руб.
| | февраль
| март
| февраль
| март
| | Молоко,л
|
|
|
|
| | Яйца, шт.
|
|
| 1,5
| 1,3
| | Картофель, кг
|
|
|
|
| Требуется определить:
- Индивидуальные индексы цен и количества товаров.
- Индекс цен Пааше.
- Индекс цен Ласпейреса.
- Индекс физического объема продукции.
Задача №2. Имеются следующие данные о заработной плате работников по трем отраслям экономики работа:
| Отрасль экономики
| Заработная плата, руб.
| Число работников, чел
| | февраль
| октябрь
| февраль
| октябрь
| | Здравоохранение
|
|
|
|
| | Культура и искусство
|
|
|
|
| | Образование
|
|
|
|
| Исчислить индекс заработной платы переменного, постоянного состава и структурных сдвигов.
Задача №3. Имеем данные о продаже товаров в розничной торговле работа, представленные в таблице 1.
| Товар
| Продано в I квартале, млн.руб.
| Снижение количества продаж во II квартале по сравнению с I, %
| | Обувь
| 8,5
| -15
| | Трикотаж
| 6,0
| -25
| Исчислить: 1. Общий индекс физического объема товарооборота (количество продаж во II кв. и I кв.).
2. Среднее изменение цен на товары, если известно, что товарооборот в фактических ценах за это время вырос на 5%.
| Проработка учебного материала. Решение задач. Умение делать выводы.
Проработка учебного материала. Решение задач. Умение делать выводы.
|
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




