|
|
ЛЕКЦІЇ З ТЕОРІЇ ЙМОВІРНОСТЕЙ ДЛЯ ФЕТСтр 1 из 5Следующая ⇒ ЛЕКЦІЇ З ТЕОРІЇ ЙМОВІРНОСТЕЙ ДЛЯ ФЕТ Первісні поняття. Подія Теорія ймовірностей вивчає математичну модель реального випробування, наслідок якого неможливо заздалегідь передбачити. При цьому припускається, що таке випробування може бути повторено необмежену кількість разів при незмінних основних умовах. Комплекс другорядних умов, які неможливо проконтролювати, змінюється від випробування до випробування. Саме ці умови приводять до того, що результати однотипних випробувань можуть бути різними.
Означення 1. Випадкова подія(далі просто подія) – будь-який факт, який може наставати чи не наставати в результаті проведення випробування, причому заздалегідь невідомо, чи з’явиться він чи ні (тобто, подія є непередбаченим результатом випробування). Для кожної випадкової події A і кожної елементарної події Означення 2. Подію A можна розглядати як підмножину W, яка складається з тих точок Рисунок 1.1 відповідає тому випадку, коли елементарна подія w1 сприяє події A, а елементарна подія w2
ної або зчисленної (такої, яку можна перерахувати) кількості точок, а у другому – із незчисленної кількості точок. Приклад 1. Підкидається гральний кубик (кубик, зроблений з однорідного матеріалу, грані якого позначені числами 1,2,3,4,5,6). Результатом випробування (спостереження) є число, що випало на верхній грані кубика. Простір W складається з шести точок wi, де через wi позначено елементарні події, що відповідають випаданню грані, на якій написано число i (i=1,2,3,4,5,6): W{w1,w2,w3,w4,w5,w6}. Події A (випадання парного числа) сприяють елементарні події w2, w4, w6 – A{w2,w4,w6}. Приклад 2. Монета підкидається тричі..Елементарні події мають вигляд Означення 3-4. Подія, що наступає при будь-якому наслідку випробування, називається вірогідною. Вона співпадає з множиною W і позначається надалі також літерою W. Подія, яка не наступає ні при жодному з наслідків випробування називається неможливою. Вона співпадає з пустою множиною і надалі позначається символом Æ. В умовах прикладу 1 випадання не більше шести очок – вірогідна подія, а випадання семи очок – неможлива. Відзначимо, що коли дискретний простір W якогось випробування складається з n точок, то кількість всіх подій, пов’язаних з цим випробуванням дорівнює 2n. Інакше кажучи, множина усіх підмножин множини, яка містить n елементів, складається з Означення 5. Подія Алгебра випадкових подій Множина, на якій означені операції суми та добутку подій, в математиці називається алгеброю. У просторі W означимо поняття суми та добутку подій. Алгебра подій дає математичний опис можливих наслідків випробування. Означення 1. Подія, яка полягає в тому, що наступає принаймні одна з подій А або B, називається об¢єднанням або сумоюцих подій(рис.1.3, а, б,в). Таку подію будемо позначати АÈB або A+B.
Означення 2. Подія, яка полягає в тому, що наступають обидві події А та B, називається перерізом або добутком цих подій (рис.1.3, а,б,г). Таку подію будемо позначати А Ç B або A·B. Із означення операцій È та Ç випливають такі співвідношення: А + А=А, А Операції + та а) Означення 3. Події АтаB називаються несумісними, якщо їх переріз є неможливою подією: A Зрозуміло, якщо події АтаB є несумісними, то будуть несумісними також події А·C іB·C. Означення 4. Попарно несумісні події Аi (i=1,2,...,n) утворюють повну систему подій (розбиття W), якщо їх сума є вірогідною подією: А1+А2+...+Аn= W, Аi·Аk = Æ (i¹k). Події А та` А + Приклад 3. Проводяться два постріли по мішені. Позначимо через Аi (i=1,2) подію, що полягає у попаданні по мішені при i-тому пострілі. Потрібно виразити через Аi події А таB, які відповідно означають, що в мішені буде: а) точно одна А пробоїна; б) хоча б одна пробоїна. Розв’язання. а) А =
Умовна ймовірність Нехай АтаB є подіями, пов’язаними з деяким випробуванням і P(B)>0. Означення 1. Умовною ймовірністю P(АïB) події А за умови здійснення події B називається відношення
Умовна ймовірність задовольняє аксіомам імовірності 1-3 пункту1.2.2:
якщо Із співвідношення (1) негайно випливає теорема множення ймовірностей
Якщо поміняти А і В місцями, то теорема множення може бути записана у вигляді
Теорема множення дозволяє знайти ймовірність добутку подій, якщо із змісту задачі зрозумілі (або обчислюються) значення умовних ймовірностей. Вона узагальнюється на випадок скінченного числа множників. Наприклад,
Приклад 1. Ймовірність аварії при запуску ракети дорівнює 0,15. Ймовірність аварії на старті є 0,12. Яка ймовірність аварії при умові успішного старту. Розв’язання. Нехай подія A полягає у тому, що запуск ракети успішний, а подія B - це успішний старт ракети. Із умов задачі випливає, що A·B=A. Отже,
Таким чином, P( Означення 2. Подія А називається незалежною від події B, якщо P(АïB)=P(А) (P(B)>0). Нехай подія А незалежна від події B і P(A)>0. Тоді з формул (2) та (2¢) випливає, що подія B незалежна від події А. Таким чином, поняття незалежності подій є взаємним. Події А та B незалежні тоді і тільки тоді, коли виконується рівність
Якщо події А та B незалежні, то будуть незалежними такі пари подій: ` А та B, А та ` B, ` А та ` B (наприклад, незалежність подій А та ` B можна довести таким чином
Якщо події A i B (P(A)>0,P(B)>0) несумісні, то вони є залежними:
Відзначимо, що коли Р(А)=0,то події А і В є незалежними:
У тому випадку, коли кількість подій перевищує два, вводиться поняття незалежних у сукупності(взаємно незалежних) подій. Останнє означає, що ймовірність якої-небудь події не залежить від здійснення інших. Наприклад, для трьох подій А1, А2, А3, незалежних у сукупності, повинні виконуватись співвідношення P(A1/A2)=P(A1), P(A1/A3)=P(A1), P(A1/A2·A3)=P(A1), P(A2/A3)=P(A2), P(A2/A1·A3)=P(A2), P(A3/A1·A2)=P(A3). Для подій А1, А2,..., Аn, незалежних у сукупності, справедливе співвідношення
Приклад 2. Проводиться два постріли по мішені. Ймовірності влучення при першому та другому пострілі дорівнюють відповідно 0.3 і 0.6. Яка ймовірність, що у мішені буде: а) точно одна пробоїна; б) хоча б одна пробоїна? Розв’язання. Позначимо через Ai (i=1,2) подію, яка полягає у тому, що при i–му пострілі буде попадання у мішень. Події A1 та A2 незалежні, але сумісні. а) Нехай A – подія, яка полягає у тому, що у мішені буде точно одна пробоїна. Тоді
=0.54. б) Нехай B – подія, яка полягає у тому, що в мішені буде хоча б одна пробоїна. Тоді B=A1+A2 і на підставі теорем додавання та множення ймовірностей матимемо
Інший спосіб розв’язку:
Формула повної ймовірності
Доведення. Оскільки W=H1ÈH2È...ÈHn, то подію A можна представити у вигляді суми попарно несумісних подій A = A·H1ÈA·H2È...ÈA·Hn рис.1.5). Послідовно застосовуючи теореми додавання та множення ймовірностей (формулу 3 з аксіом ймовірності розділу 1.2 та формулу (2) розділу 1.3), одержимо:
Якщо P(А Приклад 1. Футбольна команда грає за схемою 1-4-2-4. Ймовірність забити пенальті для нападника 0.8, півзахисника 0.7, захисника 0.6, вратаря 0.5. Знайти ймовірність того, шо навмання обраний ігрок забиває пенальті. Розв’язання. Нехай подія А – навмання обраний ігрок забиває пенальті. Призначимо гіпотези:
Рис.1.7 |

Випадкові вектори
Регресія
Якщо ми знаємо розподіл однієї координати дискретного випадкового вектора при умові, що інша координата приймає певне значення: 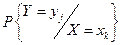 ,
,  , то можна ввести поняття умовного математичного сподівання.
, то можна ввести поняття умовного математичного сподівання.
Означення 1.Умовним математичним сподіванням 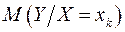 випадкової величини Y при умові, що випадкова величина Х прийняла одно з своїх можливих значень
випадкової величини Y при умові, що випадкова величина Х прийняла одно з своїх можливих значень  називається число, яке знаходиться за формулою
називається число, яке знаходиться за формулою
 (12)
(12)
Аналогічно визначається умовне математичне сподівання  .
.
При зміні х від  до
до  взагалі кажучи, змінюється умовне математичне сподівання
взагалі кажучи, змінюється умовне математичне сподівання  яке можна розглядати у цьому випадку як функцію х:
яке можна розглядати у цьому випадку як функцію х:
 . (13)
. (13)
Ця функція називається регресією У на X (Y відносно X), а її графік  - лінією регресії Y на X. Лінія регресії описує зміну середніх значень випадкової величини У при переході від одного значення Х до іншого.
- лінією регресії Y на X. Лінія регресії описує зміну середніх значень випадкової величини У при переході від одного значення Х до іншого.
Аналогічно визначається регресія Х на У (Х відносно У) і лінія регресії Х на У: 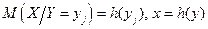 .
.
Для побудови рівняння регресії за означенням (12)-(13) необхідно знати закон розподілу двовимірного випадкового вектора (таблицю з розділа 1.2). На практиці дослідник звичайно має у своєму розпорядженні лише виборку  пар чисел скінченного об’єму
пар чисел скінченного об’єму  та рівняння регресії визначається методом найменших квадратів (МНК). Доведено, що одержана по МНК функція
та рівняння регресії визначається методом найменших квадратів (МНК). Доведено, що одержана по МНК функція  є найкращим наближенням до дійсної лінії регресії
є найкращим наближенням до дійсної лінії регресії  .
.
Випадкові величини X та У називаються лінійно корельованими, якщо лінії регресії є прямими. Рівняння цих прямих такі:
 (У на X) (14)
(У на X) (14)
 (X на У) (1
(X на У) (1  )
)
Якщо лінія регресії У на X (X на У)не є прямою, можна використати першу (другу) із прямих регресії (14)- (1  ) в якості наближення до істинної лінії регресії. У цьому випадку ця пряма називається прямою наближеної регресії. У зв'язку з цим відзначимо, що функція
) в якості наближення до істинної лінії регресії. У цьому випадку ця пряма називається прямою наближеної регресії. У зв'язку з цим відзначимо, що функція 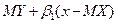 (функція
(функція  ) єнайкращим наближенням до Y (до X)серед усіх лінійних функцій випадкової величини X (випадкової величини У).
) єнайкращим наближенням до Y (до X)серед усіх лінійних функцій випадкової величини X (випадкової величини У).
Кутові коефіцієнти  та
та  прямих регресії (14)- (1
прямих регресії (14)- (1  ) називаються відповідно коефіцієнтами регресії У на X та X на У. При цьому
) називаються відповідно коефіцієнтами регресії У на X та X на У. При цьому
 ,
,  (15)
(15)
Прямі регресії (14)- (1  ) проходять через точку з координатами (MX; MY), При
) проходять через точку з координатами (MX; MY), При  прямі регресії співпадають, а при
прямі регресії співпадають, а при  - паралельні осям координат.
- паралельні осям координат.
Приклад 4. Задан закон розподілу дискретного випадкового вектора  .
.
1. Знайти а) закони розподілу його координат  и
и  ; б) їх математичні сподівання та дисперсії; в) кореляційний момент
; б) їх математичні сподівання та дисперсії; в) кореляційний момент  ; г) коефіціент кореляції
; г) коефіціент кореляції  .
.
2. Знайти умовні розподіли  та з’ясувати, чи залежні
та з’ясувати, чи залежні  та
та  .
.


| |||
| -4 | 0.4 | 0.05 | 0.1 |
| -1 | 0.05 | 0.2 | 0.2 |
3. Побудувати функцію регресії  . Знайти рівняння лінійної регресії
. Знайти рівняння лінійної регресії  на
на  та порівняти її на графику з функцією регресії
та порівняти її на графику з функцією регресії
Розв’язання. 1. а) На підставі формули (1) одержимо розподіли координат  та
та  .
.

| -4 | -1 |

| 0.55 | 0.45 |

| |||

| 0.45 | 0.25 | 0.3 |
б) 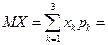 0
0  0.45+2
0.45+2  0.25+4
0.25+4  0.3=1.7;
0.3=1.7;
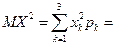 4
4  0.25+16
0.25+16  0.3=5.8;
0.3=5.8;  5.8-2.89=2.91;
5.8-2.89=2.91;
 -4
-4  0.55-1
0.55-1  0.45=-2.65;
0.45=-2.65;  (-4
(-4 
 0.55+(-1
0.55+(-1 
 0.45=8.8+0.45=9.25;
0.45=8.8+0.45=9.25;
 9.25-(2.65
9.25-(2.65  =9.25-7.0225=2.2275.
=9.25-7.0225=2.2275.
в)  =2
=2  (-4)
(-4)  0.05+4
0.05+4  (-4)
(-4)  0.1+2
0.1+2  (-1)
(-1)  0.2+4
0.2+4  (-1)
(-1)  0.2=-0.4-1.6-0.4-0.8=-3.2. К (Х, У) =М (Х
0.2=-0.4-1.6-0.4-0.8=-3.2. К (Х, У) =М (Х  У) -МХ
У) -МХ  МУ =-3.2-1.7
МУ =-3.2-1.7  (-2.65) = -3.2+4.505=1.305.
(-2.65) = -3.2+4.505=1.305.
г)  =
=  .
.
2. Знайдемо умовні розподіли  (
( =1,...,
=1,...,  ,
,  =1,...,
=1,...,  ;
;  =2,
=2,  =3), умовні закони розподілу
=3), умовні закони розподілу  та умовні математичні сподівання
та умовні математичні сподівання  для
для  =0,
=0,  =2,
=2,  =4.
=4.
а)  =0. Оскільки
=0. Оскільки  =-4/
=-4/  =0}
=0}  =
=  =
=  , а
, а
 =-1/
=-1/  =0}=
=0}=  =
=  , то умовний закон розподілу
, то умовний закон розподілу  =0}:
=0}:

| -4 | -1 |

| 8/9 | 1/9 |
,а умовне математичне сподівання  =- 4
=- 4 

б)  =2. Оскільки
=2. Оскільки  =-4/
=-4/  =2}=
=2}=  =
=  , а
, а  =-1/
=-1/  =2}=
=2}=  =
=  , то умовний закон розподілу
, то умовний закон розподілу  :
:

| -4 | -1 |

| 1/5 | 4/5 |
,а умовне математичне сподівання
 =-4
=-4 
 -1
-1 
 =-
=-  .
.
в)  =4. Оскільки
=4. Оскільки  =
=  =
=  , а
, а  =
=  =
=  , то умовний закон розподілу
, то умовний закон розподілу  : а умовне математичне сподівання
: а умовне математичне сподівання

| -4 | -1 |

| 1/3 | 2/3 |
 =-4
=-4 
 -1
-1 
 =-2.
=-2.
Оскільки, наприклад,  =-4/ Х =0}=
=-4/ Х =0}= 

 =-4}=0.55, то випадкові величини Х та У - залежні.
=-4}=0.55, то випадкові величини Х та У - залежні.
3. Функція регресії, тобто залежність умовного математичного сподівання 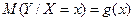 від
від  задається таблицею:
задається таблицею:
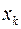
| |||

| -11/3 | -8/5 | -2 |
Рівняння прямої регресії У на Х має вигляд  +
+  , де
, де  =
=  0.45, aбо у =-2.65+0.45(х-1.7), aбо у =-3.415+0.45х. (*) Пряма регресії проходить через точку (МХ; МУ)=(1.7;-2.65). Другу точку на прямій одержимо, поклавши в рівнянні (*) х =0. Тоді друга точка: (0;-3.415). На рис.4 зображені функція регресії
0.45, aбо у =-2.65+0.45(х-1.7), aбо у =-3.415+0.45х. (*) Пряма регресії проходить через точку (МХ; МУ)=(1.7;-2.65). Другу точку на прямій одержимо, поклавши в рівнянні (*) х =0. Тоді друга точка: (0;-3.415). На рис.4 зображені функція регресії  та пряма регресії.
та пряма регресії.
.. 
Рис.4
ЛЕКЦІЇ З ТЕОРІЇ ЙМОВІРНОСТЕЙ ДЛЯ ФЕТ
Первісні поняття. Подія
Теорія ймовірностей вивчає математичну модель реального випробування, наслідок якого неможливо заздалегідь передбачити. При цьому припускається, що таке випробування може бути повторено необмежену кількість разів при незмінних основних умовах. Комплекс другорядних умов, які неможливо проконтролювати, змінюється від випробування до випробування. Саме ці умови приводять до того, що результати однотипних випробувань можуть бути різними.
 Позначимо через W множину всіх можливих взаємно виключних наслідків випробування (припускаємо, що ця множина є відомою до здійснення випробування). Множина W та її різні підмножини використовуються при побудові імовірнісної моделі цього випробування. МножинуW називають простором елементарних подій. При цьому, кожному наслідку випробування ставиться у відповідність одна і тільки одна точка простору W – елементарна подія w.
Позначимо через W множину всіх можливих взаємно виключних наслідків випробування (припускаємо, що ця множина є відомою до здійснення випробування). Множина W та її різні підмножини використовуються при побудові імовірнісної моделі цього випробування. МножинуW називають простором елементарних подій. При цьому, кожному наслідку випробування ставиться у відповідність одна і тільки одна точка простору W – елементарна подія w.
Означення 1. Випадкова подія(далі просто подія) – будь-який факт, який може наставати чи не наставати в результаті проведення випробування, причому заздалегідь невідомо, чи з’явиться він чи ні (тобто, подія є непередбаченим результатом випробування). Для кожної випадкової події A і кожної елементарної події  можна сказати, сприяє чи ні елементарна подія
можна сказати, сприяє чи ні елементарна подія  появі події A.
появі події A.
Означення 2. Подію A можна розглядати як підмножину W, яка складається з тих точок  , що сприяють появі події A.
, що сприяють появі події A.
Рисунок 1.1 відповідає тому випадку, коли елементарна подія w1 сприяє події A, а елементарна подія w2
| не сприяє. Множина W може бути як дискретною (рис.1.2,а), так і неперервною (рис.1.2,б,в). У першому випадку вона складається із скінчен- |  Рис.1.2
Рис.1.2
|
ної або зчисленної (такої, яку можна перерахувати) кількості точок, а у другому – із незчисленної кількості точок.
Приклад 1. Підкидається гральний кубик (кубик, зроблений з однорідного матеріалу, грані якого позначені числами 1,2,3,4,5,6). Результатом випробування (спостереження) є число, що випало на верхній грані кубика.
Простір W складається з шести точок wi, де через wi позначено елементарні події, що відповідають випаданню грані, на якій написано число i (i=1,2,3,4,5,6): W{w1,w2,w3,w4,w5,w6}. Події A (випадання парного числа) сприяють елементарні події w2, w4, w6 – A{w2,w4,w6}.
Приклад 2. Монета підкидається тричі..Елементарні події мають вигляд  , де
, де  – Г або Ц. Простір W{ГГГ, ГГЦ, ГЦГ, ЦГГ, ГЦЦ, ЦГЦ, ЦЦГ, ЦЦЦ}, Подія В випадання не менщ двох гербів В{ГГГ, ГГЦ, ГЦГ, ЦГГ}.
– Г або Ц. Простір W{ГГГ, ГГЦ, ГЦГ, ЦГГ, ГЦЦ, ЦГЦ, ЦЦГ, ЦЦЦ}, Подія В випадання не менщ двох гербів В{ГГГ, ГГЦ, ГЦГ, ЦГГ}.
Означення 3-4. Подія, що наступає при будь-якому наслідку випробування, називається вірогідною. Вона співпадає з множиною W і позначається надалі також літерою W. Подія, яка не наступає ні при жодному з наслідків випробування називається неможливою. Вона співпадає з пустою множиною і надалі позначається символом Æ. В умовах прикладу 1 випадання не більше шести очок – вірогідна подія, а випадання семи очок – неможлива.
Відзначимо, що коли дискретний простір W якогось випробування складається з n точок, то кількість всіх подій, пов’язаних з цим випробуванням дорівнює 2n. Інакше кажучи, множина усіх підмножин множини, яка містить n елементів, складається з  елементів
елементів
Означення 5. Подія  , яка полягає в тому, що подія А не наступає, називається п ротилежною події А або запереченням А (
, яка полягає в тому, що подія А не наступає, називається п ротилежною події А або запереченням А ( доповнює множину А до W:
доповнює множину А до W:  =W\А). Зрозуміло, що
=W\А). Зрозуміло, що  = А,
= А,  =Æ.В умовах прикладу 1 подія
=Æ.В умовах прикладу 1 подія  {w1,w3,w5}.
{w1,w3,w5}.
Алгебра випадкових подій
Множина, на якій означені операції суми та добутку подій, в математиці називається алгеброю. У просторі W означимо поняття суми та добутку подій. Алгебра подій дає математичний опис можливих наслідків випробування.
Означення 1. Подія, яка полягає в тому, що наступає принаймні одна з подій А або B, називається об¢єднанням або сумоюцих подій(рис.1.3, а, б,в). Таку подію будемо позначати АÈB або A+B.
а б в Рис. 1.3. г |
Означення 2. Подія, яка полягає в тому, що наступають обидві події А та B, називається перерізом або добутком цих подій (рис.1.3, а,б,г). Таку подію будемо позначати А Ç B або A·B.
Із означення операцій È та Ç випливають такі співвідношення:
А + А=А, А  А=А, А + W=W, А
А=А, А + W=W, А  W=А, А
W=А, А  (B + С)=(А
(B + С)=(А  B) +(А
B) +(А  С).
С).
Операції + та  пов‘язані одна з одною двома важливими формулами:
пов‘язані одна з одною двома важливими формулами:
а)  , б)
, б) 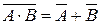 . (1)
. (1)
Означення 3. Події АтаB називаються несумісними, якщо їх переріз є неможливою подією:
A 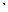 B= Æ. (2)
B= Æ. (2)
Зрозуміло, якщо події АтаB є несумісними, то будуть несумісними також події А·C іB·C.
Означення 4. Попарно несумісні події Аi (i=1,2,...,n) утворюють повну систему подій (розбиття W), якщо їх сума є вірогідною подією:
А1+А2+...+Аn= W, Аi·Аk = Æ (i¹k).
Події А та`  утворюють повну систему подій:
утворюють повну систему подій:
А +  = W, А
= W, А  =Æ.
=Æ.
Приклад 3. Проводяться два постріли по мішені. Позначимо через Аi (i=1,2) подію, що полягає у попаданні по мішені при i-тому пострілі. Потрібно виразити через Аi події А таB, які відповідно означають, що в мішені буде: а) точно одна А пробоїна; б) хоча б одна пробоїна.
Розв’язання. а) А =  (доданки суми є несумісними подіями); б) В =А1+А2(доданки суми є сумісними подіями) або В =
(доданки суми є несумісними подіями); б) В =А1+А2(доданки суми є сумісними подіями) або В =  (доданки суми є несумісними подіями, але не утворюють повної системи подій).
(доданки суми є несумісними подіями, але не утворюють повної системи подій).


Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом...

ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры...

Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все...

Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор...
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: