Расчет круглого бруса на изгиб с кручением

В случае расчета круглого бруса при действии изгиба и круче­ния (рис. 34.3) необходимо учитывать нормальные и касательные на­пряжения, т. к. максимальные значения напряжений в обоих случаях возникают на поверхности. Расчет следует вести по теории проч­ности, заменяя сложное напряженное состояние равноопасным про­стым.

Максимальное напряжение кручения в сечении

Максимальное напряжение изгиба в сечении

По одной из теорий прочности в зависимости от материала бруса рассчитывают эквивалентное напряжение для опасного сечения и проверяют брус на прочность, используя допускаемое напряжение изгиба для материала бруса.

Для круглого бруса моменты сопротивления сечения следую­щие:

При расчете по третьей теории прочности, теории максималь­ных касательных напряжений, эквивалентное напряжение рассчи­тывается по формуле

Теория применима для пластичных материалов.

При расчете по теории энергии формоизменения эквивалентное напряжение рассчитывается по формуле

Теория применима для пластичных и хрупких материалов.

Эквивалентное напряжение при расчете по теории энергии формоизменения:

где — эквивалентный момент.

Условие прочности

Примеры решения задач

Пример 1. Для заданного напряженного состояния (рис. 34.4), пользуясь гипотезой максимальных касательных напряжений, вычислить ко­эффициент запаса прочности, если σ_Т = 360 Н/мм².

Контрольные вопросы и задания

1. Чем характеризуется и как изображается напряженное состо­яние в точке?

2. Какие площадки и какие напряжения называют главными?

3. Перечислите виды напряженных состояний.

4. Чем характеризуется деформированное состояние в точке?

5. В каких случаях возникают предельные напряженные состо­яния у пластичных и хрупких материалов?

6. Что такое эквивалентное напряжение?

7. Поясните назначение теорий прочности.

8. Напишите формулы для расчета эквивалентных напряжений при расчетах по теории максимальных касательных напряжений и теории энергии формоизменения. Поясните, как ими пользоваться.

ЛЕКЦИЯ 35

Тема 2.7. Расчет бруса круглого поперечного сечения при сочетании основных деформаций

Знать формулы для эквивалентных напряжений по гипотезам наибольших касательных напряжений и энергии формоизменения.

Уметь рассчитывать брус круглого поперечного сечения на прочность при сочетании основных деформаций.

Формулы для расчета эквивалентных напряжений

Эквивалентное напряжение по гипотезе максимальных каса­тельных напряжений

Эквивалентное напряжение по гипотезе энергии формоизмене­ния

где

Условие прочности при совместном действии изгибаи кручения

где М_ЭКВ — эквивалентный момент.

Эквивалентный момент по гипотезе максимальных касательных напряжений

Эквивалентный момент по гипотезе энергии формоизменения

Особенность расчета валов

Большинство валов испытывают сочетание деформаций изгиба и кручения. Обычно валы — прямые брусья с круглым или кольце­вым сечением. При расчете валов касательные напряжения от дей­ствия поперечных сил не учитывают из-за их незначительности.

Расчеты проводят по опасным поперечным сечениям. При про­странственном нагружении вала пользуются гипотезой независимо­сти действия сил и изгибающие моменты рассматривают в двух вза­имно перпендикулярных плоскостях, а суммарный изгибающий мо­мент определяют геометрическим суммированием.

Примеры решения задач

Решение

Строим эпюры нормальных напряжений от действия изгибаю­щих моментов относительно осей Ох и Оу и эпюру касательных на­пряжений от кручения (рис. 35.2).

Максимальное касательное напряжение возникает на поверхно­сти. Максимальные нормальные напряжения от момента М_х возни­кают в точке А, максимальные нормальные напряжения от момента М_у в точке В. Нормальные напряжения складываются, потому что изгибающие моменты во взаимно перпендикулярных плоскостях гео­метрически суммируются.

Суммарный изгибающий момент:

Рассчитываем эквивалентный момент по теории максимальных касательных напряжений:

Условие прочности:

Момент сопротивления сечения: W_oceвoe = 0,1 • 60³ = 21600мм³.

Проверяем прочность:

Прочность обеспечена.

Пример 2. Из условия прочности рассчитать необходимый диа­метр вала. На валу установлены два колеса. На колеса действуют две окружные силы F_t1 = 1,2кН; F_t2 = 2кН и две радиальные силы в вертикальной плоскости F_r1 = 0,43кН; F_r2 = 0,72кН (рис. 35.3). Диаметры колес соответственно равны d₁ = 0,1м; d₂ = 0,06 м.

Принять для материала вала [ σ ] = 50МПа.

Рассчитать размеры вала кольцевого сечения при с = 0,8 (с = d_вн / d).

Расчет провести по гипотезе максимальных каса­тельных напряжений. Весом вала и колес пренебречь.

Решение

Указание. Используем принцип независимости действия сил, составляем расчетные схемы вала в вертикальной и горизонтальной плоскостях. Определяем реакции в опорах в горизонтальной и вертикальной плоскостях в отдельности. Строим эпюры изгиба­ющих моментов (рис. 35.4). Под действием окружных сил вал скручивается. Определяем действующий на валу крутящий момент.

Составим расчетную схему вала (рис. 35.4).

1. Крутящий момент на валу:

2. Изгиб рассматриваем в двух плоскостях: горизонтальной (пл. Н) и вертикальной (пл. V).

В горизонтальной плоскости определяем реакции в опоре:

Определяем изгибающие моменты в точках С и В:

В вертикальной плоскости определяем реакции в опоре:

Определяем изгибающие моменты в точках С и В:

Суммарные изгибающие моменты в точках С и В:

В точке В максимальный изгибающий момент, здесь же дей­ствует и крутящий момент.

Расчет диаметра вала ведем по наиболее нагруженному сечению.

3. Эквивалентный момент в точке В по третьей теории прочности

4. Определяем диаметр вала круглого поперечного сечения из условия прочности

Округляем полученную величину: d = 36 мм.

Примечание. При выборе диаметров вала пользоваться стандартным рядом диаметров (Приложение 2).

5. Определяем необходимые размеры вала кольцевого сечения при с = 0,8, где d — наружный диаметр вала.

Диаметр вала кольцевого сечения можно определить по форму­ле

Примем d = 42 мм.

Перегрузка незначительная. d_BH = 0,8d = 0,8 • 42 = 33,6мм.

Округляем до значения d_BH = 33 мм.

6. Сравним затраты металла по площадям сечения вала в обоих случаях.

Площадь поперечного сечения сплошного вала

Площадь поперечного сечения полого вала

Площадь поперечного сечения сплошного вала почти в два раза больше вала кольцевого сечения:

Пример 3. Определить размеры поперечного се­чения вала (рис. 2.70, а) привода управления. Усилие от тяги педали P₃, усилия, передаваемые механизмом P₁, Р₂, Р₄. Материал вала — сталь СтЗ с пределом те­кучести σ_т = 240 Н/мм², требуемый коэффициент запаса [ n ] = 2,5. Расчет выполнить по гипотезе энергии формо­изменения.

Решение

Рассмотрим равновесие вала, предварительно приведя силы Р₁, Р₂, Р₃, Р₄ к точкам, лежащим на его оси.

Перенося силы Р₁ параллельно самим себе в точки К и E, надо добавить пары сил с моментами, равными моментам сил Р₁ относительно точек К и Е, т. е.

Эти пары сил (моменты) условно показаны на рис. 2.70, б в виде дугообразных линий со стрелками. Аналогично при переносе сил Р₂, Р₃, Р₄ в точки K, E, L, Н надо добавить пары сил с моментами

Опоры вала, изображенного на рис. 2.70, а, надо рассматривать как пространственные шарнирные опоры, препятствующие перемещениям в направлении осей х и у (выбранная система координат показана на рис. 2.70, б).

Пользуясь расчетной схемой, изображенной на рис. 2.70, в, составим уравнения равновесия:

Составим проверочное уравнение:

следовательно, опорные реакции Н_А и Н_В определены верно.

Эпюры крутящих моментов М_z и изгибающих момен­тов М_у представлены на рис. 2.70, г. Опасным является сечение слева от точки L.

Условие прочности имеет вид:

где эквивалентный момент по гипотезе энергии формо­изменения

Требуемый наружный диаметр вала

Принимаем d = 45 мм, тогда d₀ = 0,8 _* 45=36 мм.

Пример 4. Проверить прочность промежуточного вала (рис. 2.71) цилиндрического прямозубого редуктора, если вал передает мощность N = 12,2 кВт при частоте вращения п = 355 об/мин. Вал изготовлен из стали Ст5 с пределом текучести σ _т = 280 Н/мм². Требуемый коэф­фициент запаса [ n ] = 4. При расчете применить гипотезу наибольших касательных напряжений.

Указание. Окружные усилия Р₁ и Р₂ лежат в горизонталь­ной плоскости и направлены по касательным к окружностям зубчатых колес. Радиальные усилия T₁ и Т₂ лежат в верти­кальной плоскости и выражаются через соответствующее окружное усилие следующим образом: T = 0,364 Р.

Решение

На рис. 2.71, а представлен схематический чертеж вала; на рис. 2.71, б показана схема вала и усилия, возникающие в зубчатом зацеплении.

Определим момент, передаваемый валом:

где

Очевидно, m = m₁ = m₂ (скручивающие моменты, приложен­ные к валу, при равномерном вращении равны по вели­чине и противоположны по направлению).

Определим усилия, действующие на зубчатые колеса.

Окружные усилия:

Радиальные усилия:

Рассмотрим равновесие вала АВ, предварительно при­ведя силы Р₁ и Р₂ к точкам, лежащим на оси вала.

Перенося силу Р₁ параллельно самой себе в точку L, надо добавить пару сил с моментом, равным моменту силы Р₁ относительно точки L, т. е.

Эта пара сил (момент) условно показана на рис. 2.71, в в виде дугообразной линии со стрелкой. Аналогично при переносе силы Р₂ в точку К надо присоединить (добавить) пару сил с моментом

Опоры вала, изображенного на рис. 2.71, а, надо рассматривать как пространственные шарнирные опоры, препятствующие линейным перемещениям в направлениях осей х и у (выбранная система координат показана на рис, 2.71, б).

Пользуясь расчетной схемой, изображенной на рис. 2.71, г, составим уравнения равновесия вала в вер­тикальной плоскости:

откуда

откуда

Составим проверочное уравнение:

следовательно, опорные реакции в вертикальной плоско­сти определены верно.

Рассмотрим равновесие вала в горизонтальной пло­скости:

откуда

откуда

Составим проверочное уравнение:

следовательно, опорные реакции в горизонтальной пло­скости определены верно.

Эпюры крутящих моментов М_z и изгибающих момен­тов М_х и М_у представлены на рис. 2.71, д.

Опасным является сечение К (см. рис. 2.71, г, д). Эквивалентный момент по гипотезе наибольших касатель­ных напряжений

Эквивалентное напряжение по гипотезе наибольших касательных напряжений для опасной точки вала

Коэффициент запаса

что значительно больше [ n ] = 4, следовательно, прочность вала обеспечена.

При расчете вала на прочность не учтено изменение напряжений во времени, поэтому и получился такой зна­чительный коэффициент запаса.

Пример 5. Определить размеры поперечного се­чения бруса (рис. 2.72, а). Материал бруса — сталь 30XГС с условными пределами текучести при растяжении и сжатии σ_о,_2р = σ_тр = 850 Н/мм², σ_0,2c = σ_Tc = 965 Н/мм². Коэффициент запаса [ n ] = 1,6.

Решение

Брус работает на совместное действие рас­тяжения (сжатия) и кручения. При таком нагружении в поперечных сечениях возникают два внутренних силовых фактора: продольная сила и крутящий момент.

Эпюры продольных сил N и крутящих моментов M_z показаны на рис. 2.72, б, в. В данном случае определить положение опасного сечения по эпюрам N и M_z невоз­можно, так как размеры поперечных сечений участков бруса различны. Для выяснения положения опасного сечения следует построить эпюры нормальных и макси­мальных касательных напряжений по длине бруса.

По формуле

вычисляем нормальные напряжения в поперечных сече­ниях бруса и строим эпюру о (рис. 2.72, г).

По формуле

вычисляем максимальные касательные напряжения в по­перечных сечениях бруса и строим эпюру т _тах (рис* 2.72, д).

Вероятно, опасными являются точки контура попереч­ных сечений участков АВ и CD (см. рис. 2.72, а).

На рис. 2.72, e показаны эпюры σ и τ для попереч­ных сечений участка АВ.

Напомним, в данном случае (брус круглого попереч­ного сечения работает на совместное действие растяже­ния — сжатия и кручения) равноопасными являются все точки контура поперечного сечения.

На рис. 2.72, ж показаны напряжения на исходных площадках в опасной точке.

Главные напряжения в опасной точке участка АВ:

 

По гипотезе прочности Мора эквивалентное напряже­ние для опасной точки этого участка

На рис. 2.72, з показаны эпюры а и т для попереч­ных сечений участка CD.

На рис. 2.72, и показаны напряжения на исходных площадках в опасной точке.

Главные напряжения в опасной точке участка CD:

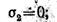
По гипотезе прочности Мора эквивалентное напряже­ние для опасной точки рассматриваемого участка

Опасными оказались точки контура поперечных сече­ний участка АВ.

Условие прочности имеет вид:

откуда

 

Пример 2.76. Определить допускаемое значение силы Р из условия прочности стержня ВС (рис.2.73).Материал стержня — чугун с пределом проч­ности при растяжении σ_вр = 150 Н/мм² и пре­делом прочности при сжатии σ_вс = 450 Н/мм². Требуемый коэффициент запаса [ n ] = 5.

Указание. Ломаный брус АBС расположен в го­ризонтальной плоскости, при­чем стержень AВ перпенди­кулярен к ВС. Силы Р, 2Р, 8Р лежат в вертикальной плоскости; силы 0,5 Р, 1,6 Р — в горизонтальной и перпендикулярны стержню ВС; силы 10Р, 16Р совпада­ ют с осью стержня ВС; пара сил с моментом m = 25Pd распо­ложена в вертикальной плоскости, перпендикулярной оси стерж­ня ВС.

Решение

Приведем силы Р и 0,5Р к центру тяжести поперечного сечения В.

Перенося силу Р параллельно самой себе в точку В, надо добавить пару сил с моментом, равным моменту силы Р относительно точки В, т. е. пару с моментом m₁ = 10 Pd.

Силу 0,5Р переносим вдоль ее линии действия в точку В.

Нагрузки, действующие на стержень ВС, показаны на рис. 2.74, а.

Строим эпюры внутренних силовых факторов для стержня ВС. При указанном нагружении стержня в его поперечных сечениях их возникает шесть: продольная сила N, поперечные силы Qx и Qy, крутящий момент Mz изгибающие моменты Мх и Му.

Эпюры N, Мz, Мх, Му представлены на рис. 2.74, б (ординаты эпюр выражены через Р и d).

Эпюры Qy и Qx не строим, так как касательные напряжения, соответствующие поперечным силам, имеют малую величину.

В рассматриваемом примере положение опасного сечения не очевидно, Предположительно, опасны сечения К (конец участка I) и С.

Опасной является точка L. Напряжения на исходных площадках в точке L (рис. 2.74, г):

По гипотезе прочности Мора эквивалентное напряжение для точки L

Определим величину и плоскость действия изгибающего момента Ми в сечении С, изображенном отдельно на рис. 2.74, д. На этом же рисунке показаны эпюры σ_И, σ_N, τ для сечения С.

Напряжения на исходных площадках в точке Н (рис. 2.74, е)

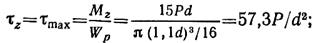
Главные напряжения в точке Н:

По гипотезе прочности Мора эквивалентное напряже­ние для точки Н

Напряжения на исходных площадках в точке Е (рис. 2.74, ж):

Главные напряжения в точке Е:

По гипотезе прочности Мора эквивалентное напряже­ние для точки Е

Опасной оказалась точка L, для которой

Условие прочности имеет вид:

откуда

Контрольные вопросы и задания

1. Какое напряженное состояние возникает в поперечном сече­нии вала при совместном действии изгиба и кручения?

2. Напишите условие прочности для расчета вала.

3. Напишите формулы для расчета эквивалентного момента при расчете по гипотезе максимальных касательных напряжений и гипо­тезе энергии формоизменения.

4. Как выбирается опасное сечение при расчете вала?

ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала...

Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...

ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования...

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: