Поверхности второго порядка. Сфера. Цилиндр
  Поверхностью второго порядка в пространстве Поверхностью второго порядка в пространстве  называется поверхность, определяемая уравнением второй степени относительно текущих координат называется поверхность, определяемая уравнением второй степени относительно текущих координат   Здесь Здесь  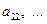 – действительные числа, называемые коэффициентами. В зависимости от коэффициентов это уравнение может определять поверхность или точку (например, уравнению – действительные числа, называемые коэффициентами. В зависимости от коэффициентов это уравнение может определять поверхность или точку (например, уравнению  отвечает точка отвечает точка 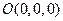 ) или пару плоскостей (например, уравнению ) или пару плоскостей (например, уравнению  отвечает пара плоскостей отвечает пара плоскостей  и и 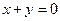 ), а также может не определять никакого множества точек (например, ), а также может не определять никакого множества точек (например,  ). Рассмотрим частные виды поверхностей второго порядка. ). Рассмотрим частные виды поверхностей второго порядка.
Сфера с центром в точке  и радиусом и радиусом  имеет уравнение имеет уравнение  где где  – заданные числа (см. рис. 32). Раскрыв скобки и перенеся число – заданные числа (см. рис. 32). Раскрыв скобки и перенеся число  в левую часть, получим в левую часть, получим   Нетрудно проверить, что уравнение второй степени относительно Нетрудно проверить, что уравнение второй степени относительно  в котором коэффициенты при в котором коэффициенты при  равны между собой, а члены с произведениями координат отсутствуют, представляет собой уравнение сферы (если не имеет место случай, когда это уравнение не определяет поверхность). равны между собой, а члены с произведениями координат отсутствуют, представляет собой уравнение сферы (если не имеет место случай, когда это уравнение не определяет поверхность).
Цилиндры второго порядка. Цилиндрической называется поверхность, описываемая прямой, остающейся параллельной некоторому направлению и пересекающей данную линию. Последняя называется направляющей цилиндрической поверхности, а прямая – образующей.
 Пусть, например, образующие цилиндрической поверхности параллельны оси Пусть, например, образующие цилиндрической поверхности параллельны оси  и направляющей служит эллипс (рис. 33) в плоскости и направляющей служит эллипс (рис. 33) в плоскости  с уравнением с уравнением
 . (57) . (57)
 Эта поверхность называется эллиптическим цилиндром. Пусть Эта поверхность называется эллиптическим цилиндром. Пусть 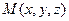 – произвольная точка этого цилиндра, а точка – произвольная точка этого цилиндра, а точка  – проекция – проекция  на плоскость на плоскость  Ясно, что абсциссы и ординаты точек Ясно, что абсциссы и ординаты точек  и и  совпадают. Так как точка совпадают. Так как точка  лежит на эллипсе, то её координаты лежит на эллипсе, то её координаты  и и  удовлетворяют уравнению (57). Но тогда этому уравнению удовлетворяют координаты удовлетворяют уравнению (57). Но тогда этому уравнению удовлетворяют координаты  и и  точки точки  цилиндра. Значит, (57) есть уравнение цилиндра. цилиндра. Значит, (57) есть уравнение цилиндра.
Итак, уравнение (57) на плоскости  определяет эллипс, а в пространстве определяет эллипс, а в пространстве  – эллиптический цилиндр с образующей, параллельной – эллиптический цилиндр с образующей, параллельной  направляющей которого является указанный эллипс. направляющей которого является указанный эллипс.
Изобразите самостоятельно гиперболический цилиндр с уравнением  и образующей, параллельной оси и образующей, параллельной оси  а также параболический цилиндр с уравнением а также параболический цилиндр с уравнением  и образующей, параллельной оси и образующей, параллельной оси 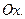
Эллипсоид
Эллипсоидом называется поверхность, определяемая уравнением
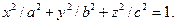 (58) (58)
где  – заданные положительные числа. Исследуем форму этой поверхности методом сечений. – заданные положительные числа. Исследуем форму этой поверхности методом сечений.
При сечении поверхности (58) плоскостью  ( (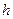 – постоянная, – постоянная,  ), проходящей через точку ), проходящей через точку  на оси на оси  параллельно плоскости параллельно плоскости  получим кривую, которая определяется совокупностью двух уравнений получим кривую, которая определяется совокупностью двух уравнений
 или или 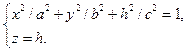
В первом уравнении перенесём  вправо и поделим обе части уравнения на вправо и поделим обе части уравнения на  получим получим
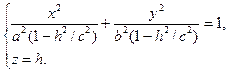
Эта система уравнений определяет эллипс с полуосями  и и  расположенный в плоскости расположенный в плоскости  При При  значения значения 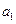 и и  очевидно, достигают своих наибольших значений очевидно, достигают своих наибольших значений  и и  т. е. на плоскости т. е. на плоскости  получаем эллипс наибольших размеров. При получаем эллипс наибольших размеров. При  значения значения 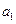 и и 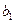 достигают наименьших значений достигают наименьших значений  и и  Это означает, что плоскости Это означает, что плоскости  и и  имеют с эллипсоидом по одной общей точке имеют с эллипсоидом по одной общей точке  и и  соответственно. При соответственно. При 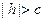 эллипсоид с плоскостью эллипсоид с плоскостью  общих точек не имеет. Аналогичная картина будет при сечении эллипсоида плоскостью общих точек не имеет. Аналогичная картина будет при сечении эллипсоида плоскостью  ( ( ) и плоскостью ) и плоскостью 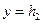 ( (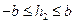 ). ).
 При При  имеем эллипсоид вращения (рис. 34). Эта поверх-ность получается при вращении вокруг оси имеем эллипсоид вращения (рис. 34). Эта поверх-ность получается при вращении вокруг оси  эллипса эллипса  расположен-ного в плоскости расположен-ного в плоскости 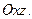
 §20. Конус §20. Конус
Конусом второго порядка называется поверхность, определяемая уравнением
 (59) (59)
 где где  – заданные положительные числа (см. рис. 35). Исследовав форму этой поверхности, как и эллипсоида, методом сечений, получим, что при сечении плоскостью – заданные положительные числа (см. рис. 35). Исследовав форму этой поверхности, как и эллипсоида, методом сечений, получим, что при сечении плоскостью  ( (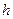 – постоянная) получается эллипс с полуосями – постоянная) получается эллипс с полуосями  и и  Очевидно, что при Очевидно, что при   т. е. конус (59) имеет с плоскостью т. е. конус (59) имеет с плоскостью  одну общую точку – начало координат. С уве-личением одну общую точку – начало координат. С уве-личением  значения значения  и и  увеличи-ваются. Покажем теперь, что при сечении поверхности (59) плоскостью с урав-нением увеличи-ваются. Покажем теперь, что при сечении поверхности (59) плоскостью с урав-нением  ( ( – постоянная), прохо-дящей через – постоянная), прохо-дящей через  получается пара прямых, проходящих через начало координат. получается пара прямых, проходящих через начало координат.
В самом деле, при таком сечении получается линия, определяемая системой уравнений
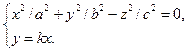
Заменим в первом уравнении  на на 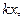 получим получим
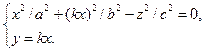
Но первое уравнение равносильно совокупности двух уравнений
 и и 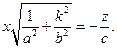
Поэтому последняя система равносильна совокупности двух систем
 и и 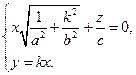
Все уравнения в этих системах определяют плоскости, проходящие через начало координат. Значит, каждая система определяет в пространстве прямую, проходящую через начало координат. При  получаем конус вращения (вокруг оси получаем конус вращения (вокруг оси  ). ).
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




