|
Коллинеарности двух векторов, площадь треугольника
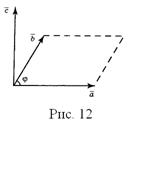
Даны два вектора  и и 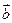 . Построим их, поместив начала в общей точке (см. рис. 12). Векторным произведением двух векторов . Построим их, поместив начала в общей точке (см. рис. 12). Векторным произведением двух векторов  и и 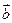 называется вектор (обозначаемый называется вектор (обозначаемый 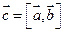 ), который обладает свойствами: ), который обладает свойствами:
·  , т. е. длина вектора , т. е. длина вектора  численно равна площади параллелограмма, построенного на численно равна площади параллелограмма, построенного на  , , 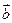 как на сторонах; как на сторонах;
·  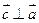 , ,  , т. е. , т. е.  перпендикулярен к плоскости указанного параллелограмма; перпендикулярен к плоскости указанного параллелограмма;
· вектор  направлен так, что если смотреть с его конца, то кратчайший поворот от первого вектора направлен так, что если смотреть с его конца, то кратчайший поворот от первого вектора  ко второму вектору ко второму вектору 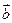 совершается против хода часовой стрелки. совершается против хода часовой стрелки.
Для векторного произведения  применяют и другие обозначения: применяют и другие обозначения:  , ,  ´ ´ 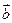 . .
Векторное произведение обладает следующими свойствами:
  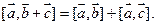
Первые два свойства доказываются построением. Докажем справедливость равенства
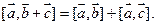
Вначале отметим, что любой вектор  можно представить в виде можно представить в виде  где вектор где вектор 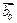 коллинеарен коллинеарен 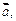 а вектор а вектор  ортогонален ортогонален 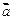 (см. рис. 13). Чтобы в этом убедиться, достаточно через начало вектора (см. рис. 13). Чтобы в этом убедиться, достаточно через начало вектора  провести прямую, параллельную провести прямую, параллельную 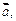 через конец вектора через конец вектора  провести плоскость, перпендикулярную провести плоскость, перпендикулярную 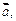 точка их пересечения служит концом точка их пересечения служит концом 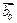 и началом и началом  (начало (начало 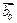 совпадает с началом совпадает с началом  , конец , конец  – с концом – с концом  ). ).
 Замечая, что площадь параллелограмма, построенного на векторах Замечая, что площадь параллелограмма, построенного на векторах 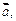  равна площади параллелограмма, построенного на векторах равна площади параллелограмма, построенного на векторах 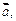 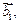 поскольку они имеют общую сторону поскольку они имеют общую сторону 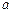 , одну и ту же высоту , одну и ту же высоту  , заключаем, что , заключаем, что
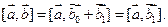
 Аналогично для вектора Аналогично для вектора  где вектор где вектор  коллинеарен коллинеарен 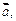 а вектор а вектор 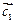 ортогонален ортогонален 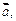 будем иметь будем иметь
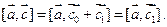
Покажем, что
 или или 
где  суть векторы, лежащие в одной плоскости, так как они перпендикулярны суть векторы, лежащие в одной плоскости, так как они перпендикулярны 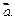 Здесь имеем Здесь имеем
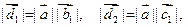
поскольку вектор 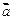 ортогонален и ортогонален и 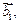 и и  Кроме того, Кроме того, 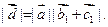 Заметим, что Заметим, что  так как вектор так как вектор  ортогонален ортогонален 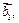 а вектор а вектор 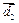 ортогонален ортогонален  Но Но 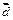 ортогонален ортогонален  поэтому угол поэтому угол 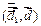 равен углу между векторами равен углу между векторами  и и  Таким образом, векторы Таким образом, векторы  получаются поворотом вокруг получаются поворотом вокруг 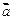 соответственно векторов соответственно векторов  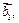 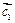 на угол, равный на угол, равный 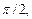 в одном и том же направлении (против хода часовой стрелки, если смотреть с конца вектора в одном и том же направлении (против хода часовой стрелки, если смотреть с конца вектора 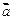 ) и умножением их на ) и умножением их на  . Это означает, что . Это означает, что  Учитывая, что Учитывая, что 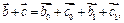 где где 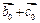 – вектор, коллинеарный – вектор, коллинеарный 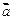 , ,  ортогонален ортогонален 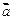 , и принимая во внимание предыдущие соотношения, будем иметь , и принимая во внимание предыдущие соотношения, будем иметь
 что и требовалось. что и требовалось.
Пусть векторы  и и  заданы своими проекциями: заданы своими проекциями:  =( =( , ,  , ,  ), ),  . Тогда . Тогда  = =   + +   + +   , ,  = =   + +   + +   . Сначала рассмотрим векторные произведения базисных векторов. . Сначала рассмотрим векторные произведения базисных векторов.
С помощью определения векторного произведения покажем справедливость равенств
[   ]= ]=  ; [ ; [  , ,  ]= ]=  ; [ ; [  , ,  ]= ]=  ; [ ; [  , ,  ]= ]= 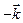 ; ;
[  , ,  ]= ]= 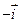 ; [ ; [  , ,  ]= ]=  ; (19) ; (19)
[  , ,  ]=0; [ ]=0; [  , ,  ]=0; [ ]=0; [  , ,  ]=0. (20) ]=0. (20)
Итак, пусть [  , ,  ]= ]=  . Вектор . Вектор  обладает свойствами: обладает свойствами:
· 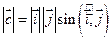 = 1×1×1 = 1; = 1×1×1 = 1;
·  , ,  , т. е. , т. е.  перпендикулярен к плоскости, в которой лежат векторы перпендикулярен к плоскости, в которой лежат векторы  и и  ; ;
·  направлен так, что если смотреть с его конца, то кратчайший поворот от первого вектора направлен так, что если смотреть с его конца, то кратчайший поворот от первого вектора  ко второму вектору ко второму вектору  совершается против хода часовой стрелки, т. е. совершается против хода часовой стрелки, т. е.  совпадает с совпадает с  , следовательно, [ , следовательно, [  , ,  ]= ]=  . .
Покажем, что [  , ,  ]=0. Пусть [ ]=0. Пусть [  , ,  ]= ]=  . Тогда . Тогда 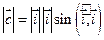 =0, =0,  =0, т. е. [ =0, т. е. [  , ,  ]=0. Аналогично доказываются остальные равенства (19) – (20). Рассмотрим векторное произведение [ ]=0. Аналогично доказываются остальные равенства (19) – (20). Рассмотрим векторное произведение [  , ,  ] = [ ] = [   + +   + +   , ,   + +   + +   ]. Использовав последние два свойства, запишем ]. Использовав последние два свойства, запишем
[  , ,  ]= ]=   [ [  , ,  ]+ ]+   [ [  , ,  ]+ ]+   [ [  , ,  ]+ ]+   [ [  , ,  ]+ ]+
+   [ [  , ,  ]+ ]+   [ [  , ,  ]+ ]+   [ [  , ,  ]+ ]+   [ [  , ,  ]+ ]+   [ [  , ,  ]. ].
Отсюда с учётом (19) – (20) имеем
[  , ,  ]= ]=            + +    + +    - -    . .
Итак,
[  , ,  ]=( ]=(  - -   ) )  -( -(  - -   ) )  +( +(  - -   ) )  . (21) . (21)
Следовательно (см. §1),
 . (22) . (22)
Эту формулу можно записать так:
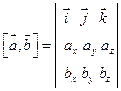 . (23) . (23)
Таким образом, если  и и 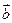 заданы своими проекциями, то векторное произведение двух векторов определяется по формуле (23). заданы своими проекциями, то векторное произведение двух векторов определяется по формуле (23).
Условие коллинеарности двух векторов. Если для ненулевых векторов выполняется условие  то то  и и  коллинеарны. коллинеарны.
В самом деле, если  то то 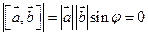 и и 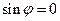 , т. е. , т. е.  или или 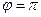 . Следовательно, векторы . Следовательно, векторы  , , 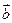 коллинеарны. коллинеарны.
В этом случае из (21) имеем   - -   =0, =0,   - -   =0, =0,   - -   =0. Значит, =0. Значит,  Это и есть условие коллине-арности двух векторов, заданных своими проекциями. Это и есть условие коллине-арности двух векторов, заданных своими проекциями.
Решим следующую задачу: определить площадь треугольника, заданного своими вершинами.
Пусть  , ,  , , 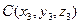 – вершины треугольника в пространстве – вершины треугольника в пространстве  , а их координаты – заданные числа. Найдем векторы (см. §7) , а их координаты – заданные числа. Найдем векторы (см. §7)   векторное произведение которых обозначим векторное произведение которых обозначим  = = 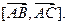 Тогда согласно (22) Тогда согласно (22)
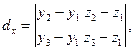 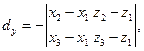 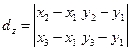
и  Площадь параллелограмма, построенного на векторах Площадь параллелограмма, построенного на векторах  и и 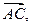 равна найденному числу равна найденному числу 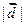 , поэтому искомая площадь треугольника определяется по формуле , поэтому искомая площадь треугольника определяется по формуле  . .
§11. Смешанное произведение векторов и его геометрический смысл. Условие компланарности трех векторов
Даны векторы  , ,  и и  . Векторы . Векторы  , ,  перемножим векторно и получим перемножим векторно и получим 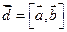 . Этот вектор умножим скалярно на . Этот вектор умножим скалярно на  и получим число и получим число  , которое называется смешанным (векторно-скалярным) произведением трёх исходных векторов , которое называется смешанным (векторно-скалярным) произведением трёх исходных векторов  , ,  , ,  и обозначается и обозначается
( , ,  , ,  ) = ) =  = =  . (24) . (24)
Рассмотрим это смешанное произведение, когда векторы заданы своими проекциями  , ,  , ,  . Проекции вектора . Проекции вектора 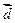 на оси координат определяются по формуле (22). на оси координат определяются по формуле (22).
Скалярное произведение векторов 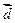 и и  равно сумме произведений одноимённых проекций: равно сумме произведений одноимённых проекций:
 . .
Левая часть этой формулы – смешанное произведение ( , ,  , ,  ). Правую часть запишем в виде определителя третьего порядка: ). Правую часть запишем в виде определителя третьего порядка:
 . (25) . (25)
Эта формула позволяет вычислить смешанное произведение векторов, заданных своими проекциями. Выясним теперь
Геометрический смысл смешанного произведения. Даны векторы  , ,  и и  . Построим эти векторы, поместив их начала в общей точке, а затем на них как на рёбрах построим параллелепипед (рис. 14). Построим вектор . Построим эти векторы, поместив их начала в общей точке, а затем на них как на рёбрах построим параллелепипед (рис. 14). Построим вектор 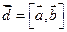 , перпендикулярный к плоскости, в которой лежат векторы , перпендикулярный к плоскости, в которой лежат векторы  и и  , т. е. перпендикулярный к нижнему основанию параллелепипеда. Длина | , т. е. перпендикулярный к нижнему основанию параллелепипеда. Длина | 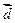 | равна площади | равна площади 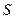 нижнего основания параллелепипеда (т. е. площади параллелограмма, построенного на нижнего основания параллелепипеда (т. е. площади параллелограмма, построенного на 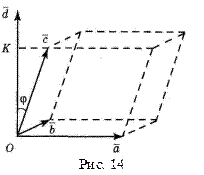 векторах векторах  и и  как на сторонах). Через конец как на сторонах). Через конец  проведём плоскость, перпендикулярную к проведём плоскость, перпендикулярную к 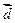 (ясно, что верхнее основание параллелепипеда лежит в этой плоскости). Эта плоскость пересечёт вектор (ясно, что верхнее основание параллелепипеда лежит в этой плоскости). Эта плоскость пересечёт вектор 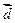 (или его продолжение) в точке К (К – проекция конца вектора (или его продолжение) в точке К (К – проекция конца вектора  на указанную линию). Из построения следует, что расстояние ОК равно высоте на указанную линию). Из построения следует, что расстояние ОК равно высоте 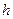 параллелепипеда. Пусть параллелепипеда. Пусть  – угол между – угол между 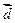 и и  . На рис. 14 изображен случай, когда . На рис. 14 изображен случай, когда  при этом при этом 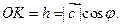 Смешанное произведение Смешанное произведение  Но Но 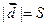 и и  Поэтому Поэтому 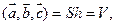 где где  – объём параллелепипеда. Этот результат мы получили для случая, когда – объём параллелепипеда. Этот результат мы получили для случая, когда 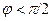 . Если . Если  , то вектор , то вектор  лежит ниже плоскости векторов лежит ниже плоскости векторов  , ,  , при этом , при этом 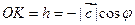 и и  Итак, справедлива формула Итак, справедлива формула
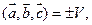 (26) (26)
где  – объем параллелепипеда. – объем параллелепипеда.
Определение. Три вектора называются компланарными, если они лежат в одной плоскости.
Условие компланарности трех векторов. Если для трёх ненулевых векторов  , ,  и и  выполняется условие выполняется условие
 , (27) , (27)
то эти векторы компланарны.
Действительно, в этом случае согласно (26) имеем 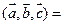 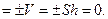 Отсюда следует, что три вектора лежат в одной плоскости, так как или Отсюда следует, что три вектора лежат в одной плоскости, так как или  или или 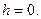
Если  , ,  и и  заданы своими проекциями, то условие компланарности (27) с учётом (25) можно записать так: заданы своими проекциями, то условие компланарности (27) с учётом (25) можно записать так:
 . .
Это условие проверяется непосредственно по заданным проекциям рассматриваемых векторов.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




