|
Общая система линейных алгебраических уравнений.
Метод Гаусса
Дана система  линейных алгебраических уравнений с линейных алгебраических уравнений с  неизвестными неизвестными 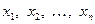
 (20) (20)
Здесь коэффициенты 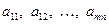 и свободные члены и свободные члены  – заданные числа. Будем считать, что число – заданные числа. Будем считать, что число  уравнений не больше числа уравнений не больше числа  неизвестных (случай неизвестных (случай  требует особого рассмотрения). требует особого рассмотрения).
Система (20) называется совместной, если она имеет решение, т. е. существуют числа 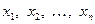 , удовлетворяющие всем уравнениям системы. Система называется несовместной, если она не имеет решения. Две системы называются равносильными (эквивалентными), если любое решение одной из них является решением другой, и наоборот. , удовлетворяющие всем уравнениям системы. Система называется несовместной, если она не имеет решения. Две системы называются равносильными (эквивалентными), если любое решение одной из них является решением другой, и наоборот.
Следующие преобразования, называемые элементарными, переводят заданную систему в равносильную (эквивалентную) ей:
· перестановка любых двух уравнений системы;
· умножение любого уравнения системы на ненулевое число;
· прибавление к обеим частям данного уравнения соответствующих частей другого уравнения, умноженных на любое ненулевое число.
Если в процессе элементарных преобразований системы (20) появится уравнение вида  , то это соотношение отбрасывается, так как ему удовлетворяют любые значения неизвестных , то это соотношение отбрасывается, так как ему удовлетворяют любые значения неизвестных 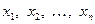 (что приводит к уменьшению числа уравнений системы). Если в процессе элементарных преобразований системы (20) появится соотношение (что приводит к уменьшению числа уравнений системы). Если в процессе элементарных преобразований системы (20) появится соотношение  , т. е. противоречивое соотношение, которое не может быть выполнено, то система (20) является несовместной. , т. е. противоречивое соотношение, которое не может быть выполнено, то система (20) является несовместной.
Метод Гаусса заключается в следующем. Пусть  (если (если  , то переставим уравнения так, чтобы в первом уравнении коэффициент при первом неизвестном не равнялся нулю или с этой же целью перенумеруем неизвестные, что приведет к перестановке соответствующих столбцов коэффициентов). Из всех уравнений, кроме первого, в системе (20) исключим неизвестную , то переставим уравнения так, чтобы в первом уравнении коэффициент при первом неизвестном не равнялся нулю или с этой же целью перенумеруем неизвестные, что приведет к перестановке соответствующих столбцов коэффициентов). Из всех уравнений, кроме первого, в системе (20) исключим неизвестную  , для этого ко второму уравнению прибавим первое, умноженное на , для этого ко второму уравнению прибавим первое, умноженное на 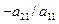 , к третьему уравнению прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на 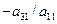 , и т. д. Тогда придём к системе вида , и т. д. Тогда придём к системе вида
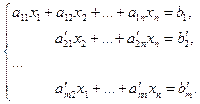
Пусть  (если (если  , то снова переставим уравнения или перенумеруем неизвестные , то снова переставим уравнения или перенумеруем неизвестные  ). Теперь аналогично предыдущему из всех уравнений, кроме первого и второго, исключим ). Теперь аналогично предыдущему из всех уравнений, кроме первого и второго, исключим  . Если система (20) совместна, т. е. при указанных преобразованиях в ней не окажется противоречивого соотношения . Если система (20) совместна, т. е. при указанных преобразованиях в ней не окажется противоречивого соотношения  , процесс продолжим. В конечном счёте путём вышеуказанных преобразований придём к одному из следующих случаев: , процесс продолжим. В конечном счёте путём вышеуказанных преобразований придём к одному из следующих случаев:
· к ступенчатой системе
 (21) (21)
здесь число уравнений  , так как система содержит неизвестные , так как система содержит неизвестные 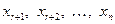 (если (если 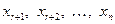 не входят в систему (21), то их не будет и в исходной системе (20)); не входят в систему (21), то их не будет и в исходной системе (20));
· к треугольной системе
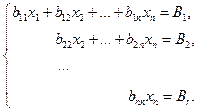 (22) (22)
В системах (21), (22) по построению все коэффициенты  отличны от нуля. В случае системы (20), приведённой к системе (22), далее поступим так: из последнего уравнения (22) найдем отличны от нуля. В случае системы (20), приведённой к системе (22), далее поступим так: из последнего уравнения (22) найдем  ; из предпоследнего найдем ; из предпоследнего найдем 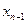 , затем , затем  , и, наконец, , и, наконец,  , т. е. найдём все искомые неизвестные. , т. е. найдём все искомые неизвестные.
Итак, в этом случае система (20) имеет единственное решение. Определитель преобразованной системы (22) обозначим  . Он равен . Он равен
  0. 0.
В последнем легко убедиться, разложив этот определитель по элементам первого столбца, в котором только один элемент (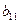 ) отличен от 0, и разложив аналогично оставшиеся миноры также по элементам первого столбца. Определитель исходной системы (20), когда ) отличен от 0, и разложив аналогично оставшиеся миноры также по элементам первого столбца. Определитель исходной системы (20), когда  , обозначим D. Он равен , обозначим D. Он равен 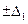 , т. е. может отличаться лишь знаком от , т. е. может отличаться лишь знаком от  . В самом деле, прибавлению к одному из уравнений системы (20) другого уравнения, умноженного на определённое число, отвечает соответствующая операция над строками определителя D, которая не изменяет этот определитель. Перестановке уравнений в исходной системе отвечает перестановка строк в определителе системы . В самом деле, прибавлению к одному из уравнений системы (20) другого уравнения, умноженного на определённое число, отвечает соответствующая операция над строками определителя D, которая не изменяет этот определитель. Перестановке уравнений в исходной системе отвечает перестановка строк в определителе системы  а перенумерации неизвестных – перестановка столбцов, каждый из которых изменит лишь знак определителя. Как видно из предыдущей формулы, а перенумерации неизвестных – перестановка столбцов, каждый из которых изменит лишь знак определителя. Как видно из предыдущей формулы, 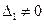 , следовательно, и , следовательно, и  . Итак, определитель системы (20) при . Итак, определитель системы (20) при  отличен от нуля, если эта система приводится к треугольной системе (22). Таким образом, при отличен от нуля, если эта система приводится к треугольной системе (22). Таким образом, при  система (20), приводящаяся к треугольной системе, имеет единственное решение и ее определитель отличен от нуля. система (20), приводящаяся к треугольной системе, имеет единственное решение и ее определитель отличен от нуля.
Пусть система (20) приводится к ступенчатой системе (21). Перенесем в ее правую часть все слагаемые, содержащие неизвестные 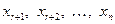 , ,
 (23) (23)
 В этой системе всем неизвестным В этой системе всем неизвестным 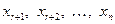 придадим произвольные (по нашему выбору) значения. Тогда в правых частях (23) будут известные числа, и из последнего уравнения найдём придадим произвольные (по нашему выбору) значения. Тогда в правых частях (23) будут известные числа, и из последнего уравнения найдём  , из предыдущего – , из предыдущего –  и т. д., найдём и т. д., найдём  . Так как значения . Так как значения 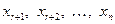 выбраны нами произвольно, то система (23), следовательно, и (20), имеет бесконечное множество решений. выбраны нами произвольно, то система (23), следовательно, и (20), имеет бесконечное множество решений.
Итак, система (20), приводимая к ступенчатой системе, имеет бесконечное множество решений.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




