|
Силовой расчет стержневых конструкций
Стержневыми будем называть конструкции, состоящие из невесомых стержней, соединенных по концам шарнирами (рис. 2.5). Соединяющий шарнир  называется узлом. К стержневым конструкциям близки конструкции из невесомых нитей (рис. 2.6), а также смешанные конструкции из невесомых стержней и нитей (рис. 2.7). Расчетные схемы у всех этих конструкций одинаковы, одинаковы и методики расчета по определению усилий в стержнях и нитях. называется узлом. К стержневым конструкциям близки конструкции из невесомых нитей (рис. 2.6), а также смешанные конструкции из невесомых стержней и нитей (рис. 2.7). Расчетные схемы у всех этих конструкций одинаковы, одинаковы и методики расчета по определению усилий в стержнях и нитях.
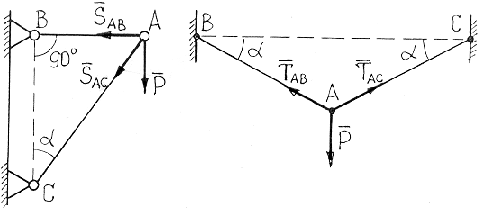
Рис. 2.5. Рис. 2.6.
 Рис. 2.7
Рис. 2.7
| В качестве объектов равновесия при расчете рассматриваемых конструкций рекомендуется брать узлы этих конструкций (узел А на рис 2.5, 2.6 и 2.7).При определении сил, действующих на узел стержневой конструкции, нужно представить, что узел – тело малых размеров (например, шарнирный болт), к которому присоединены стержни, сходящиеся в узле. Эти стержни можно рассматривать как связи, ограничивающие перемещение узла; а для определения направления реакций этих связей можно пользоваться указаниями п.п. 1.2.2 и 1.2.3.
| Все действующие на узел силы, активные и реактивные, сходятся в этом узле. Так, на узел  стержневой конструкции (рис. 2.5) действует активная сила стержневой конструкции (рис. 2.5) действует активная сила  и реакции стержней и реакции стержней 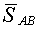 и и 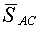 . На узел . На узел  нитяной конструкции (рис. 2.6) действует активная сила нитяной конструкции (рис. 2.6) действует активная сила 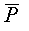 и реакции нитей и реакции нитей 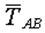 и и  . .
Координатные оси на расчетных схемах следует выбирать так, чтобы уравнения равновесия были для них наиболее простыми. Можно добиться, например, что в системе (2.1) каждое уравнение будет иметь одну неизвестную силу. Для этого оси х и у надо проводить перпендикулярно неизвестным силам.
Вычисление реакций стержней и нитей производится с использованием условий равновесия. Эти реакции равны по модулю усилиям в соответствующих стержнях и нитях. После определения реакций силовой расчет указанных конструкций считается законченным.
ЗАДАЧА 2.1. (1)
Груз Р = 100 H подвешен в точке А стрелы, закрепленной на фундаменте с помощью шарнира В. Стрела удерживается в указанном положении тросом АС. Определить, пренебрегая весом стрелы и троса, усилие в стреле и натяжение троса.
Решение:
Выбираем за объект равновесия узел А.
На узел действует вес груза  , реакция троса , реакция троса 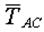 и реакция стрелы и реакция стрелы 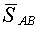 . Стрела АВ рассматривается как невесомый стержень. Направление реакций . Стрела АВ рассматривается как невесомый стержень. Направление реакций 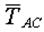 и и 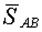 принято в соответствии с указаниями п.п. 1.2.2 и 1.2.3. Для составления уравнений равновесия (2.1) проведем через узел принято в соответствии с указаниями п.п. 1.2.2 и 1.2.3. Для составления уравнений равновесия (2.1) проведем через узел  оси оси 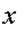 и и 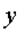 (рис. 2.7). Спроектируем силы (рис. 2.7). Спроектируем силы 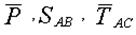 на оси. В результате получим следующие уравнения равновесия: на оси. В результате получим следующие уравнения равновесия:

 Рис. 2.8.
Рис. 2.8.
| Неизвестные силы 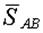 и и 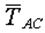 входят в оба уравнения равновесия, для их вычисления надо решать систему двух полученных уравнений. Вычисления можно упростить, если оси х и у провести перпендикулярно неизвестным силам, например, ось х – перпендикулярно входят в оба уравнения равновесия, для их вычисления надо решать систему двух полученных уравнений. Вычисления можно упростить, если оси х и у провести перпендикулярно неизвестным силам, например, ось х – перпендикулярно 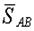 , ось у – перпендикулярно , ось у – перпендикулярно  (рис. 2.8). Для этих осей уравнения равновесия получатся следующими: (рис. 2.8). Для этих осей уравнения равновесия получатся следующими:
| 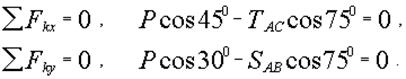
Из первого уравнения находим  H, H,
из второго – 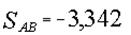 H. H.
Для реакции стрелы 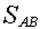 получится отрицательный результат. Это означает согласно указаниям п. 1.2.3, что стрела сжата, а не растянута, как предполагалось при выборе направления получится отрицательный результат. Это означает согласно указаниям п. 1.2.3, что стрела сжата, а не растянута, как предполагалось при выборе направления 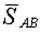 на расчетной схеме. Делать исправления на расчетной схеме и в уравнениях равновесия не рекомендуется. на расчетной схеме. Делать исправления на расчетной схеме и в уравнениях равновесия не рекомендуется.
Предлагаем определить реакции связей в расчетных схемах, изображенных на рис. 2.5 и 2.6, считая 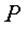 и и  заданными величинами. заданными величинами.
Ответы:
– для схемы на рис. 2.5 – 
– для схемы на рис. 2.6 – 
ЗАДАЧА 2.2 (2)
В узле  соединены три невесомые нерастяжимые нити, к свободным концам которых прикреплены грузы соединены три невесомые нерастяжимые нити, к свободным концам которых прикреплены грузы  и и 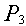 . Две нити перекинуты через неподвижные блоки . Две нити перекинуты через неподвижные блоки  и и 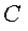 , углы наклона этих нитей к горизонту равны , углы наклона этих нитей к горизонту равны  и и  . Считая, что . Считая, что  и и  заданы, определить заданы, определить 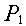 и и  при равновесии. Трение на блоках не учитывать. при равновесии. Трение на блоках не учитывать.
Решение:
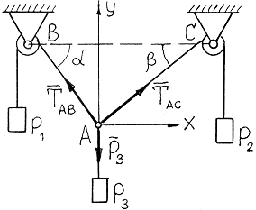 Рис. 2.9.
Рис. 2.9.
| Выберем за объект равновесия узел А. На объект действуют силы  . Направления реакций нитей приняты в соответствии с указаниями п. 1.2.2. Учтем, что при отсутствии трения на блоках . Направления реакций нитей приняты в соответствии с указаниями п. 1.2.2. Учтем, что при отсутствии трения на блоках  . Для составления уравнений равновесия (2.1) проведем через узел . Для составления уравнений равновесия (2.1) проведем через узел  оси оси  и и 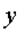 (рис. 2.9). Спроектируем силы (рис. 2.9). Спроектируем силы 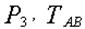 и и 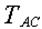 на оси, учитывая указания п. 2.1.1. В результате получим следующие уравнения равновесия: на оси, учитывая указания п. 2.1.1. В результате получим следующие уравнения равновесия:
| 
Неизвестные силы 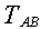  и и  входят в оба уравнения равновесия. Из первого уравнения найдем: входят в оба уравнения равновесия. Из первого уравнения найдем:
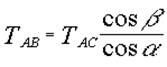 . (а) . (а)
Подставив это соотношение во второе уравнение равновесия, после несложных преобразований получим
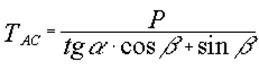 . .
Теперь из соотношения (а) можно определить 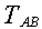 . .
Искомые  и и 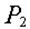 равны соответственно равны соответственно 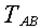 и и 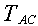 . .
В данной задаче оси координат проведены традиционно: ось  – по горизонтали, ось – по горизонтали, ось  – по вертикали. Если оси – по вертикали. Если оси 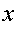 и и  провести перпендикулярно неизвестным силам, как это сделано в предыдущей задаче, то возникнут трудности при определении величин углов между силами и осями координат, В рассмотренном решении этих трудностей нет, поэтому оно предпочтительнее. провести перпендикулярно неизвестным силам, как это сделано в предыдущей задаче, то возникнут трудности при определении величин углов между силами и осями координат, В рассмотренном решении этих трудностей нет, поэтому оно предпочтительнее.
Как видим, выбор направления осей зависит от особенностей задачи. В некоторых задачах следует рассматривать несколько вариантов выбора осей.
ЗАДАЧА 2.3 (4)
Груз Р = 300 Н равномерно поднимается лебедкой D с помощью веревки, перекинутой через блок С. Ось блока поддерживается стержнями АС и ВС. Пренебрегая размерами блока, весом стержней и веревки, определить усилия в стержнях АС и ВС. Трение на блоке не учитывать.
Решение:
Груз Р движется равномерно и прямолинейно, поэтому можно считать, что груз и вся конструкция находится в состоянии равновесия. Это значит, мы вправе для решения задачи применить условия равновесия статики.
За объект равновесия принимаем узел С. Размерами блока по условию задачи можно пренебречь, поэтому будем считать, что сила 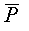 и реакция веревки и реакция веревки 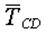 проходят через узел С. Кроме этих двух сил на узел действуют также реакции стержней проходят через узел С. Кроме этих двух сил на узел действуют также реакции стержней 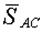 и и  . То есть, в данной задаче можно считать, что на объект действует система сходящихся сил. Направления реакций приняты в соответствии с указаниями п.п. 1.2.2 и 1.2.3. . То есть, в данной задаче можно считать, что на объект действует система сходящихся сил. Направления реакций приняты в соответствии с указаниями п.п. 1.2.2 и 1.2.3.
 Рис. 2.10.
Рис. 2.10.
| Часто в задачах на равновесие конструкций с блоком допускается ошибка: при расстановке сил не учитывается реакция веревки, удерживающая груз на блоке (рис. 2.10 – это реакция 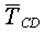 ). Такое, конечно, допускать нельзя, – ведь без силы ). Такое, конечно, допускать нельзя, – ведь без силы 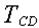 веревка и груз Р в равновесии быть не могут. Более того, при равновесии сила веревка и груз Р в равновесии быть не могут. Более того, при равновесии сила 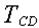 по модулю должна быть равна весу груза Р. Это тоже надо учитывать при решении задач. по модулю должна быть равна весу груза Р. Это тоже надо учитывать при решении задач.
| Ось х (рис. 2.10) направим так, чтобы она была перпендикуляра неизвестной силе 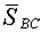 , Уравнение равновесия для этой оси следующее: , Уравнение равновесия для этой оси следующее:
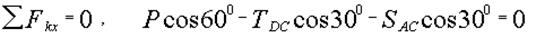 . .
Отсюда, учитывая, что 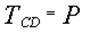 , находим , находим 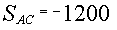 H. H.
При выборе направления второй оси, учтем что величина 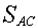 уже найдена и любая ось, непараллельная оси х дает уравнение равновесия с одним неизвестным уже найдена и любая ось, непараллельная оси х дает уравнение равновесия с одним неизвестным 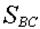 . Направим ось y по вертикали, так как в этом случае уравнение равновесия будет очень простым: . Направим ось y по вертикали, так как в этом случае уравнение равновесия будет очень простым:
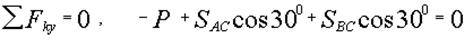 . .
Отсюда 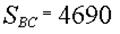 Н. Н.
Отметим, что при решении задачи 1 оси х и y были выбраны перпендикулярно неизвестным силам, в задаче 3 только ось х была выбрана перпендикулярно неизвестной силе, а ось y выбрана из условия, чтобы уравнение равновесия для нее было проще. В обоих вариантах выбора осей определение неизвестных реакций сводится к последовательному решению уравнений с одним неизвестным. Но второй вариант обычно более предпочтителен, так как уравнения равновесия в этом варианте получаются проще.
Рассмотренную методику решения задач можно применить для силового расчета стержневых конструкций, состоящих из нескольких узлов.
ЗАДАЧА 2.4 (5)
 Рис. 2.11.
Рис. 2.11.
| Стержни AC и BD (рис. 2.11), прикрепленные концевыми шарнирами A и B к опоре, соединены стержнем CD. К шарнирам C и D прикреплены нити, к свободным концам которых подвешены грузы P и Q. Определить вес груза Q так, чтобы конструкция была в равновесии, если Р = 10 kН. Весом стержней и трением на блоке пренебречь.
| Решение:
Заданная конструкция имеет два узла – C и D. Каждый из узлов может быть объектом равновесия. На узел C действуют силы: 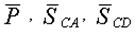 ; а на узел D – силы: ; а на узел D – силы: 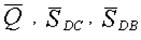 . Направление реакций стержней принято в соответствии с указаниями п. 1.2.3. Реакция стержня . Направление реакций стержней принято в соответствии с указаниями п. 1.2.3. Реакция стержня 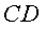 , приложенная к узлу , приложенная к узлу 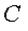 , обозначена , обозначена 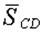 , а реакция этого же стержня, приложенная к узлу D, – , а реакция этого же стержня, приложенная к узлу D, –  . Очевидным является соотношение: . Очевидным является соотношение:  . .
Искомая сила Q приложена к узлу D, на который действуют только неизвестные силы. Поэтому начинать решение задачи надо с рассмотрения узла C, к которому приложена известная сила 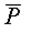 . Из условия равновесия узла C достаточно определить силу . Из условия равновесия узла C достаточно определить силу  передающуюся на узел D. Поэтому ось передающуюся на узел D. Поэтому ось 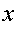 проведем перпендикулярно проведем перпендикулярно  . Для этой оси уравнение равновесия системы сил, приложенной к узлу C, имеет вид . Для этой оси уравнение равновесия системы сил, приложенной к узлу C, имеет вид
 . .
Отсюда находим  kH. Знак “-“ указывает на то, что стержень CD сжат (см. п. 1.2.3). kH. Знак “-“ указывает на то, что стержень CD сжат (см. п. 1.2.3).
Переходим теперь к узлу D. Из условия равновесия узла D нужно найти только силу Q, поэтому ось 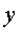 проведем перпендикулярно проведем перпендикулярно 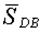 . Для этой оси уравнение равновесия имеет вид . Для этой оси уравнение равновесия имеет вид
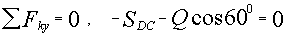 . .
Отсюда находим  kH. kH.
Силовой расчет пространственных стержневых конструкций выполняется по аналогичным методикам.
ЗАДАЧА 2.5. (6)
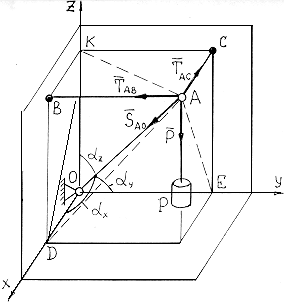 Рис. 2.12.
Рис. 2.12.
| Стержень AO, шарнирно закрепленный в вершине О прямоугольного трехгранного угла, удерживается в наклонном положении тросами AB и AC, перпендикулярными соответствующим граням трехгранного угла. 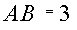 м, м,  м, м, 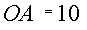 м. К узлу A прикреплен груз м. К узлу A прикреплен груз  Н. Определить усилия в стержне и тросах, пренебрегая их весом. Н. Определить усилия в стержне и тросах, пренебрегая их весом.
| Решение:
За объект равновесия принимаем узел A, На узел действуют четыре силы: активная сила 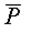 , реакции тросов , реакции тросов 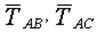 и стержня и стержня  . Направления реакций приняты в соответствии с указаниями п.п. 1.2.2 и 1.2.3. . Направления реакций приняты в соответствии с указаниями п.п. 1.2.2 и 1.2.3.
При составлении уравнений равновесия будем следовать рекомендациям п. 2.1.

Значения косинусов углов 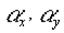 и и  найдем из прямоугольных треугольников найдем из прямоугольных треугольников 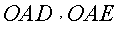 и и  . .
Из уравнений равновесия находим
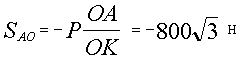 , ,
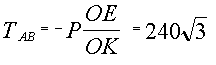 Н, Н,
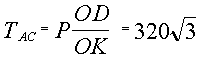 Н. Н.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




