|
|
Представление функции в виде ряда Фурье
Рис. 8.1
Такой сигнал характеризуется амплитудой Аm, периодом t и основной частотой ω (её называют ещё угловой, и круговой), связанной с периодом t соотношением: ω = 2π t–1. Из курса математики известно, что периодическую функцию можно разложить в ряд Фурье, имеющий две формы записи. Первая из них имеет вид:
где k – номер гармоники ряда; А0 – постоянная составляющая или нулевая гармоника ряда; Вk – коэффициенты синусных составляющих; Аk – коэффициенты косинусных составляющих. Гармоникой называется синусная или косинусная составляющая частоты kω. Коэффициенты
Вторая форма записи ряда Фурье имеет вид:
где Сk – амплитуда k–ой гармоники; ψk – начальная фаза k–ой гармоники. Параметры Сk и ψk связаны с коэффициентами Вk и Аk соотношениями:
Частоту k–ой гармоники обозначают ωk. Она связана с номером k соотношением: ωk = k·ω. Период k–ой гармоники обозначают Тk. Он связан с номером k обратной зависимостью: Тk.= k–1·Т.
Например, сигнал а(t) имеет три гармоники:
Построим графики трех гармоник и суммарного сигнала в одних осях
Рис. 8.1 Суммарная периодическая функция (сплошная линия) имеет период, равный периоду 1-ой гармоники. Расчет схем с источниками негармонического Периодического сигнала Для многих негармонических функций составлены справочники для раз- ложения их в ряд Фурье. В справочниках дается сам ряд и его коэффициенты Аk, Вk или Сk и ψk. Если мы имеем дело с каким–либо специальным сигналом, то его коэффициенты можно получить машинным методом. Практически все языки программирования включают в себя преобразование Фурье в качестве стандартных программ. В наших расчетах мы будем иметь дело с уже заданным рядом Фурье для периодического негармонического сигнала источника. Если в схему включен источник э.д.с., сигнал которого представлен рядом Фурье:
то такому источнику соответствует эквивалентная схема из последовательно включенных э.д.с.(рис. 8.2):
Рис. 8.2 Здесь
n – число гармоник, не считая нулевой, подлежащих учету. На основании метода наложения в представленной эквивалентной схеме ток (или напряжение) можно рассчитать для каждой гармоники отдельно в частичных схемах. Для перехода к частичной схеме k–ой гармоники остальные источники заменяются их внутренними сопротивлениями, то есть коротко замкну- тыми соединениями (рис. 8.3):
Рис. 8.3
Если в исходной схеме включен источник тока, сигнал которого представлен рядом Фурье вида:
то такому источнику соответствует схема из параллельно включенных источников тока. На основании метода наложения в эквивалентной схеме искомый ток можно найти путем расчета n+1 частичных схем по каждой из гармоник отдельно. Для определения полного негармонического тока (или напряжения) во временной области необходимо определить искомую функцию в каждой частичной схеме, а затем сложить их, например: i(t) = i(0) + i(1)(t) + i(2)(t) + … + i(n)(t). При проведении расчетов токов и напряжений в области комплексных чисел нельзя складывать токи (или напряжения) разных гармоник, так как условием перехода из временной области в частотную является равенство частот всех токов (или напряжений), то есть ω = const. Поэтому отсутствует понятие комплексного тока или напряжения негармонической функции. Однако, каждую частичную схему для k–ой гармоники можно представить в комплексной форме. Для перехода к комплексной схеме k–ой гармоники необходимо определить, как и раньше: 1) комплексное действующее или комплексное амплитудное значение э.д.с. k–ой гармоники:
или
2) комплексные сопротивления реактивных элементов L и С:
3) обозначить токи и напряжения комплексными амплитудными или комплексными действующими значениями Каждая частичная схема в комплексной форме рассчитывается относительно тока или напряжения любым удобным способом. Если в исходной схеме включены измерительные приборы (амперметр или вольтметр), то необходимо определить действующее значение периодического негармонического тока или напряжения. На основании общего определения действующего значения периодического негармонического тока или напряжения можно записать:
После подстановки негармонических функций тока или напряжения в виде ряда Фурье под интеграл и преобразований получим формулы:
где i, u – действующее значение тока или напряжения негармонического I(0), U(0) – нулевая гармоника или постоянная составляющая исследуемого I(k), U(k) – действующее значение k–ой гармоники исследуемого тока или
Отметим, что для нулевой гармоники существует только действующее значение. Итак, алгоритм расчета схемы с источником негармонического периодического сигнала сводится к следующему. 1. Представляем функцию сигнала источника в виде ряда Фурье (если он не задан). 2. Переходим к частичным схемам для каждой гармоники, входящей в ряд Фурье. Для гармоник больше нулевой переходим к комплексным схемам. 3. Рассчитываем каждую частичную схему относительно искомого тока или напряжения. 4. Если в схеме включены амперметры или вольтметры, то определяем действующее значение гармонических токов или напряжений по приведенным формулам. 5. Если в исходной схеме требуется определить ток или напряжение во временнόй области, то необходимо найти частичные токи или напряжения во временнόй области, а затем их сложить.
e(t) = 10 + 10Sin100t + 8Sin(200t + определить показание вольтметра и построить временнýю диаграмму напряжения на вольтметре, если R = 100 Ом, L = 1 Гн, С = 100 мкФ.
Согласно приведенному алгоритму, первый пункт выполнять не нужно, так как ряд Фурье для сигнала е(t) уже задан. Переходим к частичным схемам. Их будет столько, сколько гармоник входит в ряд фурье сигнала е(t). Нулевая гармоника k = 0 (рис. 8.5)
На постоянном токе индуктивность заменя- ется коротко замкнутым соединением, а ем-
Первая гармоника k = 1 (рис. 8.6)
     ω = 100 рад·с–1; ψ1 = 0; ω = 100 рад·с–1; ψ1 = 0; 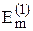 = 10 В; = 10 В;

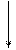
    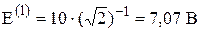 ; ;
  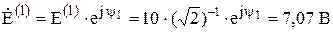 ; ;
 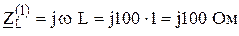 ; ;
Вторая гармоника k = 2 (рис. 8.7)
     ω2 = 200 рад·с–1; ψ2 = ω2 = 200 рад·с–1; ψ2 = 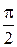 ; ; 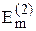 = 8 В; = 8 В;
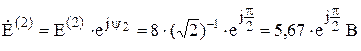 ; ;
Определяем напряжение на вольтметре для каждой гармоники из частичных схем. k = 0 k = 1
На частоте первой гармоники наблюдается резонанс напряжений:
k = 2
Показания вольтметра
Напряжение на вольтметре, как функция времени:
На рис. 8.8 приведены временные (волновые) диаграммы гармонических составляющих и сигнала
Рис. 8.8 Нулевая гармоника 10 В (штриховая линия). Первая гармоника
  Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...  ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры...  Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...  Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|