|
Знаходження характеристик варіації та форми розподілу
Для кожного інтервалу знаходимо відхилення його середини  від середньої від середньої  за відповідною формулою. Так, наприклад, різницю за відповідною формулою. Так, наприклад, різницю 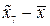 обчислюємо за формулою “=J10-$H$13”, як показано на рис. 1.14. Знайдені значення обчислюємо за формулою “=J10-$H$13”, як показано на рис. 1.14. Знайдені значення 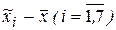 заносимо у комірки L4:L10. заносимо у комірки L4:L10.
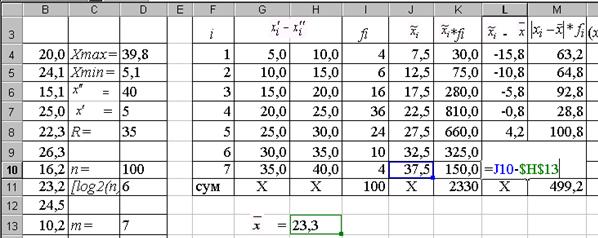
Рис. 1.14.
Для кожного інтервалу за відповідною формулою знаходимо добуток модуля відхилення на його частоту. Так, наприклад, значення  обчислюємо за формулою “=ABS(L4)*I4”. Знайдені значення обчислюємо за формулою “=ABS(L4)*I4”. Знайдені значення 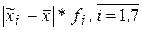 заносимо у комірки, наприклад, М4:М10 (рис. 1.15). заносимо у комірки, наприклад, М4:М10 (рис. 1.15).
У комірку М11 заносимо суму знайдених значень, обчислену за допомогою функції “СУММ (М4:М10)”.
Зауважимо, що обчислення можна проводити з округленням результатів до необхідної кількості знаків за допомогою функції “ОКРУГЛ”:
ОКРУГЛ (число;число_разрядов),
де “число”— число, що округлюється;
“число_разрядов” – необхідне число десяткових знаків, яке виконавець вибирає на власний розсуд, ураховуючи порядок чисел, що округлюються.
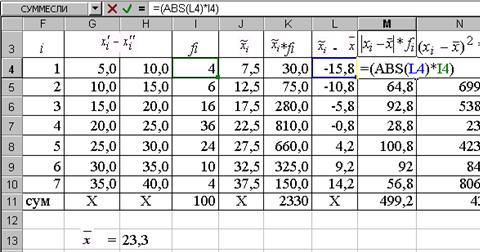
Рис. 1.15.
У даному прикладі всі вищенаведені розрахунки проведені точно, без округлень.
Для кожного інтервалу знаходимо добутки другого, третього та четвертого степенів відхилень середин інтервалів від середньої на відповідні частоти. Обчислені значення заносимо у комірки відповідно N4:N10, O4:O10, P4:P10. У комірках N11, O11 та Р11 обчислюються відповідні суми, як показано на рис. 1.16.
При цьому числа, що знаходяться у комірках Р4:Р11, округлено до 3-х десяткових знаків, а всі інші наведені без округлень (рис. 1.16).
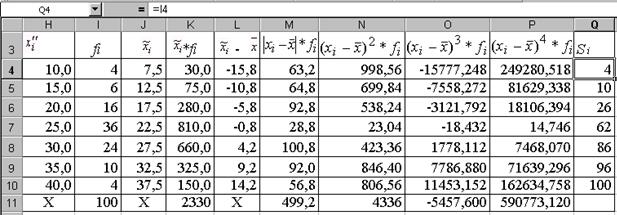
Рис. 1.16.
Після обчислення необхідних сум знаходимо за відповідними формулами, округлюючи до двох десяткових знаків: середнє лінійне відхилення d, дисперсію D, середнє квадратичне відхилення 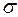 , квадратичний , квадратичний 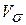 та лінійний та лінійний 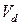 коефіцієнти варіації, коефіцієнт осциляції коефіцієнти варіації, коефіцієнт осциляції 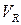 , коефіцієнти асиметрії As та ексцесу Ex у комірках, наприклад, G15:G22. Розрахунки виконуємо шляхом введення відповідних формул у відповідні комірки. , коефіцієнти асиметрії As та ексцесу Ex у комірках, наприклад, G15:G22. Розрахунки виконуємо шляхом введення відповідних формул у відповідні комірки.
Так, наприклад, коефіцієнт осциляції 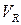 знаходимо за формулою “=ОКРУГЛ(D8/H13;2)”, як показано на рис 1.17, а коефіцієнт ексцесу Ex за формулою “=ОКРУГЛ(P11/(G17^4*D10);2)”. знаходимо за формулою “=ОКРУГЛ(D8/H13;2)”, як показано на рис 1.17, а коефіцієнт ексцесу Ex за формулою “=ОКРУГЛ(P11/(G17^4*D10);2)”.
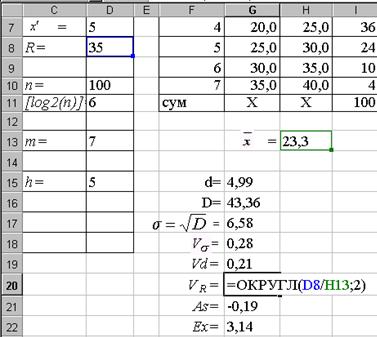
Рис. 1.17.
Знаходження моди та медіани
Для обчислення моди та медіани необхідно спочатку знайти модальний та медіанний інтервали побудованого і. в. р.
Очевидно, що модальним є 4-й інтервал, оскільки його частота f 4=36 найбільша.
Для знаходження медіанного інтервалу необхідно для кожного і- го 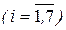 інтервалу знайти накопичену частоту Si . Очевидно, що S 1 =f 1, а Si+ 1 = Sі + fi+ 1 інтервалу знайти накопичену частоту Si . Очевидно, що S 1 =f 1, а Si+ 1 = Sі + fi+ 1 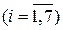 . Накопичені частоти будемо знаходити у діапазоні, наприклад Q4-Q10. Так S5 знаходимо за формулою “=Q7+І8”, як показано на рис. 1.18. . Накопичені частоти будемо знаходити у діапазоні, наприклад Q4-Q10. Так S5 знаходимо за формулою “=Q7+І8”, як показано на рис. 1.18.
Аналізуючи значення Si, легко встановити, що медіанним інтервалом є 4-й інтервал, оскільки він перший з інтервалів, для яких накопичена частота перевищує половину обсягу сукупності: 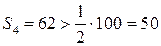 . .
Після знаходження модального та медіанного інтервалів обчислюємо моду та медіану за відповідними формулами
 , , 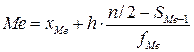 , ,
округлюючи їх значення до двох десяткових знаків.
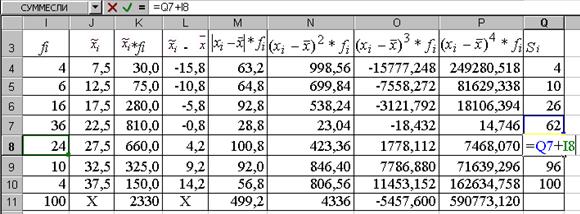
Рис. 1.18.
Для даного прикладу ці характеристики обчислюємо у комірках, наприклад, К15 та К16 за формулами відповідно
“ =ОКРУГЛ(G7+D5*((I7-I6)/(2*I7-I6-I8));2)”
“ =ОКРУГЛ(G7+D5*((D10/2-I6)/I7);2)”, як показано на рис. 1.19.
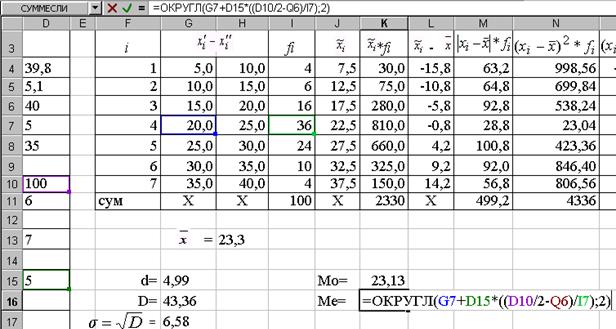
Рис. 1.19.
За результатами дослідження можна зробити висновок: маємо одновершинний унімодальний гостроверхий (Ex> 3) розподіл однорідної статистичної сукупності з незначною лівосторонньою асиметрією.
Додаток 1
Вихідні дані для лабораторних робіт № 3, 4
| № з/п
| Номери стовпців Li
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| 4,5
| 0,8
| 95,1
| 1,4
| 13,2
| 2,6
| 93,6
| 11,8
| 10,9
| 35,4
| 1,8
| 45,6
| 52,3
| 90,1
| 18,6
| |
| 7,8
| 1,2
| 95,2
| 1,6
| 11,7
| 2,7
| 92,0
| 10,9
| 10,6
| 36,2
| 1,9
| 46,3
| 54,2
| 95,6
| 19,8
| |
| 6,9
| 0,9
| 94,8
| 1,8
| 15,3
| 2,6
| 93,0
| 11,7
| 10,7
| 34,1
| 2,1
| 47,9
| 60,3
| 95,2
| 25,1
| |
| 8,4
| 1,1
| 95,0
| 1,9
| 17,4
| 3,0
| 93,4
| 11,8
| 10,6
| 33,8
| 2,3
| 49,1
| 68,9
| 96,8
| 27,3
| |
| 13,2
| 1,3
| 96,3
| 2,1
| 17,5
| 2,9
| 92,6
| 11,5
| 10,5
| 34,9
| 2,6
| 50,2
| 66,4
| 90,3
| 26,5
| |
| 11,7
| 1,2
| 94,7
| 2,3
| 18,6
| 2,8
| 91,0
| 11,6
| 10,5
| 36,4
| 2,7
| 50,3
| 65,8
| 92,4
| 29,4
| |
| 15,3
| 1,1
| 95,3
| 2,6
| 19,8
| 3,0
| 90,0
| 11,4
| 10,6
| 37,8
| 2,6
| 52,1
| 67,9
| 96,3
| 33,6
| |
| 17,4
| 1,4
| 94,2
| 2,7
| 25,1
| 3,1
| 90,8
| 11,5
| 10,3
| 36,5
| 3,0
| 52,6
| 75,2
| 95,8
| 32,1
| |
| 17,5
| 1,4
| 95,6
| 2,6
| 27,3
| 3,0
| 90,9
| 11,6
| 10,4
| 39,2
| 2,9
| 55,0
| 74,3
| 98,9
| 35,0
| |
| 18,6
| 1,5
| 93,7
| 3,0
| 26,5
| 3,1
| 91,2
| 11,5
| 10,3
| 42,0
| 2,8
| 54,2
| 77,8
| 91,2
| 38,4
| |
| 19,8
| 1,4
| 94,6
| 2,9
| 29,4
| 3,2
| 90,0
| 11,3
| 10,2
| 41,3
| 3,0
| 56,3
| 79,5
| 93,4
| 37,6
| |
| 25,1
| 1,6
| 92,1
| 2,8
| 33,6
| 3,6
| 89,9
| 11,4
| 10,1
| 43,6
| 3,1
| 57,4
| 83,6
| 95,6
| 39,8
| |
| 27,3
| 1,8
| 94,6
| 3,0
| 32,1
| 3,5
| 90,2
| 11,2
| 10,5
| 44,1
| 3,0
| 58,9
| 85,1
| 96,1
| 43,2
| |
| 26,5
| 1,9
| 93,8
| 3,1
| 35,0
| 3,6
| 88,9
| 11,1
| 10,1
| 47,2
| 3,1
| 59,6
| 90,3
| 99,4
| 42,6
| |
| 29,4
| 2,1
| 92,9
| 3,0
| 38,4
| 3,6
| 89,6
| 10,9
| 10,2
| 45,6
| 3,2
| 59,9
| 90,1
| 98,7
| 47,6
| |
| 33,6
| 2,3
| 91,8
| 3,1
| 37,6
| 3,7
| 88,4
| 11,1
| 10,0
| 46,3
| 3,6
| 62,4
| 97,5
| 99,3
| 46,5
| |
| 32,1
| 2,6
| 94,5
| 3,2
| 39,8
| 3,9
| 89,7
| 11,0
| 10,0
| 47,9
| 3,5
| 61,8
| 95,2
| 100,1
| 48,1
| |
| 35,0
| 2,7
| 93,6
| 3,6
| 43,2
| 3,8
| 87,6
| 10,9
| 10,2
| 49,1
| 3,6
| 64,8
| 96,8
| 101,2
| 50,3
| |
| 38,4
| 2,6
| 92,0
| 3,5
| 42,6
| 4,1
| 86,5
| 10,7
| –
| 50,2
| 3,6
| 66,2
| –
| –
| 50,8
| |
| 37,6
| 3,0
| –
| 3,6
| 47,6
| 4,2
| 84,3
| –
| –
| 50,3
| 3,7
| 67,0
| –
| –
| 54,9
| |
| 39,8
| 2,9
| –
| 3,6
| 46,5
| 4,4
| –
| –
| –
| 52,1
| 3,9
| –
| –
| –
| 58,7
| |
| 43,2
| –
| –
| –
| 48,1
| –
| –
| –
| –
| 52,6
| 3,8
| –
| –
| –
| 58,6
| |
| –
| –
| –
| –
| 50,3
| –
| –
| –
| –
| 55,0
| –
| –
| –
| –
| 59,4
| |
| –
| –
| –
| –
| 50,8
| –
| –
| –
| –
| –
| –
| –
| –
| –
| 61,8
|
Закінчення додатку 1
| № з/п
| Номери стовпців Li
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| 1,5
| 93,7
| 11,5
| 42,0
| 0,8
| 45,3
| 100,2
| 94,6
| 140,2
| 90,1
| 64,5
| 107,6
| 92,7
| 28,7
| 51,2
| |
| 1,4
| 94,6
| 11,3
| 41,3
| 1,2
| 44,2
| 100,1
| 97,2
| 140,3
| 97,5
| 66,8
| 109,6
| 93,6
| 27,4
| 50,6
| |
| 1,6
| 92,1
| 11,4
| 43,6
| 0,9
| 44,6
| 99,4
| 97,3
| 140,6
| 95,2
| 67,9
| 110,2
| 92,5
| 24,6
| 52,3
| |
| 1,8
| 94,6
| 11,2
| 44,1
| 1,1
| 45,8
| 99,6
| 96,1
| 139,5
| 96,8
| 69,3
| 112,4
| 93,6
| 26,3
| 50,4
| |
| 1,9
| 93,8
| 11,1
| 47,2
| 1,3
| 46,8
| 99,8
| 97,5
| 142,3
| 90,1
| 72,1
| 113,1
| 93,8
| 25,4
| 47,6
| |
| 2,1
| 92,9
| 10,9
| 45,6
| 1,2
| 48,2
| 101,6
| 96,0
| 135,6
| 95,6
| 73,4
| 114,8
| 93,4
| 24,8
| 49,2
| |
| 2,3
| 91,8
| 11,1
| 46,3
| 1,1
| 49,3
| 102,3
| 96,1
| 136,8
| 95,2
| 78,6
| 115,6
| 92,8
| 23,9
| 47,3
| |
| 2,6
| 94,5
| 11,0
| 47,9
| 1,4
| 52,4
| 106,9
| 95,9
| 135,4
| 96,8
| 81,3
| 118,3
| 93,1
| 22,8
| 45,1
| |
| 2,7
| 93,6
| 10,9
| 49,1
| 1,4
| 57,8
| 105,2
| 96,3
| 133,6
| 90,3
| 79,5
| 117,9
| 92,5
| 21,0
| 47,6
| |
| 2,6
| 92,0
| 10,7
| 50,2
| 1,5
| 56,9
| 104,6
| 95,2
| 131,0
| 92,4
| 84,9
| 117,6
| 91,2
| 20,0
| 40,3
| |
| 3,0
| 93,0
| 10,9
| 50,3
| 1,4
| 58,2
| 103,8
| 95,4
| 132,9
| 96,3
| 83,1
| 118,5
| 89,7
| 20,9
| 44,2
| |
| 2,9
| 93,4
| 10,6
| 52,1
| 1,6
| 62,3
| 105,2
| 94,2
| 132,4
| 95,8
| 86,5
| 119,3
| 91,6
| 20,3
| 45,0
| |
| 2,8
| 92,6
| 10,7
| 52,6
| 1,8
| 61,4
| 106,7
| 93,8
| 129,6
| 98,9
| 88,9
| 121,4
| 91,2
| 18,9
| 39,6
| |
| 3,0
| 91,0
| 10,6
| 55,0
| 1,9
| 64,8
| 108,9
| 94,5
| 130,0
| 91,2
| 87,4
| 122,0
| 90,8
| 19,6
| 37,2
| |
| 3,1
| 90,0
| 10,5
| 54,2
| 2,1
| 64,5
| 107,6
| 92,7
| 128,7
| 93,4
| 92,6
| 121,6
| 90,2
| 17,4
| 37,9
| |
| 3,0
| 90,8
| 10,5
| 56,3
| 2,3
| 66,8
| 109,6
| 93,6
| 127,4
| 95,6
| 93,8
| 125,3
| 89,9
| 16,8
| 40,1
| |
| 3,1
| 90,9
| 10,6
| 57,4
| 2,6
| 67,9
| 110,2
| 92,5
| 124,6
| 96,1
| 96,5
| 126,8
| 91,0
| 16,2
| 39,7
| |
| 3,2
| 91,2
| 10,3
| 58,9
| 2,7
| 69,3
| 112,4
| 93,6
| 126,3
| 99,4
| 95,6
| 128,5
| 90,5
| 15,3
| 41,3
| |
| 3,6
| 90,0
| 10,4
| 59,6
| 2,6
| 72,1
| 113,1
| 93,8
| 125,4
| 98,7
| 98,2
| 127,9
| 90,2
| 14,8
| 37,4
| |
| 3,5
| 89,9
| 10,3
| 59,9
| 3,0
| 73,4
| 114,8
| 93,4
| –
| 99,3
| 99,3
| 129,3
| 89,3
| 14,6
| 34,2
| |
| 3,6
| 90,2
| 10,2
| 62,4
| 2,9
| 78,6
| –
| 92,8
| –
| 100,1
| 99,8
| 128,5
| 89,7
| 15,9
| 35,1
| |
| –
| 88,9
| 10,1
| 61,8
| –
| 76,9
| –
| –
| –
| 101,2
| 102,5
| 127,4
| 88,2
| –
| 35,6
| |
| –
| –
| 10,5
| 64,8
| –
| –
| –
| –
| –
| 104,5
| 103,8
| 128,3
| –
| –
| 32,3
| |
| –
| –
| –
| 66,2
| –
| –
| –
| –
| –
| –
| –
| –
| –
| –
| 31,0
|
Додаток 2
Критичні значення кореляційного відношення 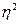 (0,05; k 1; k 2) (0,05; k 1; k 2)
і коефіцієнта детермінації 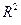 (0,05; k 1; k 2) для рівня значущості (0,05; k 1; k 2) для рівня значущості 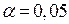
 k 1
k 2 k 1
k 2
|
|
|
|
|
| |
| 0,771
| 0,865
| 0,903
| 0,924
| 0,938
| |
| 0,658
| 0,776
| 0,832
| 0,865
| 0,887
| |
| 0,569
| 0,699
| 0,764
| 0,806
| 0,835
| |
| 0,500
| 0,632
| 0,704
| 0,751
| 0,785
| |
| 0,444
| 0,575
| 0,651
| 0,702
| 0,739
| |
| 0,399
| 0,527
| 0,604
| 0,657
| 0,697
| |
| 0,362
| 0,488
| 0,563
| 0,628
| 0,659
| |
| 0,332
| 0,451
| 0,527
| 0,582
| 0,624
| |
| 0,306
| 0,420
| 0,495
| 0,550
| 0,593
| |
| 0,283
| 0,394
| 0,466
| 0,521
| 0,564
| |
| 0,247
| 0,345
| 0,417
| 0,471
| 0,514
| |
| 0,219
| 0,312
| 0,378
| 0,429
| 0,477
| |
| 0,197
| 0,283
| 0,348
| 0,394
| 0,435
| |
| 0,179
| 0,259
| 0,318
| 0,364
| 0,404
| |
| 0,164
| 0,238
| 0,294
| 0,339
| 0,377
| |
| 0,151
| 0,221
| 0,273
| 0,316
| 0,353
| |
| 0,140
| 0,206
| 0,256
| 0,297
| 0,332
| |
| 0,130
| 0,193
| 0,240
| 0,279
| 0,314
| |
| 0,122
| 0,182
| 0,227
| 0,264
| 0,297
|
Додаток 3
Критичні точки розподілу Стьюдента 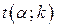
Для двосторонньої критичної області
 α
k α
k
| 0,10
| 0,05
| |
| 2,35
| 3,18
| |
| 2,13
| 2,78
| |
| 2,01
| 2,57
| |
| 1,94
| 2,45
| |
| 1,89
| 2,36
| |
| 1,86
| 2,31
| |
| 1,83
| 2,26
| |
| 1,81
| 2,23
| |
| 1,80
| 2,20
| |
| 1,78
| 2,18
| |
| 1,76
| 2,14
| |
| 1,75
| 2,12
| |
| 1,73
| 2,10
| |
| 1,73
| 2,09
| |
| 1,72
| 2,07
| |
| 1,71
| 2,06
| |
| 1,70
| 2,05
| |
| 1,68
| 2,02
| |
| 1,67
| 2,00
| |
| 1,66
| 1,98
| | ∞
| 1,64
| 1,96
|
Додаток 4
Критичні значення 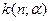 модуля коефіцієнта кореляції знаків Фехнера для двосторонньої критичної області; модуля коефіцієнта кореляції знаків Фехнера для двосторонньої критичної області; 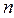 − обсяг вибірки; − обсяг вибірки; 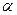 − рівень значущості − рівень значущості
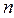
|
|
|
|
|
|
|
|
|
|
| 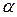
| 0,05
| 1,000
| 1,000
| 1,000
| 0,778
| 0,800
| 0,818
| 0,667
| 0,692
| 0,714
| 0,600
| | 0,10
| 1,000
| 1,000
| 0,750
| 0,778
| 0,800
| 0,636
| 0,667
| 0,538
| 0,571
| 0,600
| 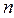
|
|
|
|
|
|
|
|
|
|
| 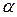
| 0,05
| 0,625
| 0,529
| 0,556
| 0,579
| 0,500
| 0,524
| 0,545
| 0,478
| 0,500
| 0,440
| | 0,10
| 0,500
| 0,529
| 0,444
| 0,474
| 0,500
| 0,429
| 0,455
| 0,391
| 0,417
| 0,440
|
Додаток 5
Таблиця значень інтегральної функції Лапласа
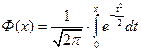
| x
| Ф(x)
| x
| Ф(x)
| x
| Ф(x)
| x
| Ф(x)
| | 0,00
| 0,0000
| 0,24
| 0,0948
| 0,48
| 0,1844
| 0,72
| 0,2642
| | 0,01
| 0,0040
| 0,25
| 0,0987
| 0,49
| 0,1879
| 0,73
| 0,2673
| | 0,02
| 0,0080
| 0,26
| 0,1026
| 0,50
| 0,1915
| 0,74
| 0,2703
| | 0,03
| 0,0120
| 0,27
| 0,1064
| 0,51
| 0,1950
| 0,75
| 0,2734
| | 0,04
| 0,0160
| 0,28
| 0,1103
| 0,52
| 0,1985
| 0,76
| 0,2764
| | 0,05
| 0,0199
| 0,29
| 0,1141
| 0,53
| 0,2019
| 0,77
| 0,2794
| | 0,06
| 0,0239
| 0,30
| 0,1179
| 0,54
| 0,2054
| 0,78
| 0,2823
| | 0,07
| 0,0279
| 0,31
| 0,1217
| 0,55
| 0,2088
| 0,79
| 0,2852
| | 0,08
| 0,0319
| 0,32
| 0,1255
| 0,56
| 0,2123
| 0,80
| 0,2881
| | 0,09
| 0,0359
| 0,33
| 0,1293
| 0,57
| 0,2157
| 0,81
| 0,2930
| | 0,10
| 0,0398
| 0,34
| 0,1331
| 0,58
| 0,2190
| 0,82
| 0,2939
| | 0,11
| 0,0438
| 0,35
| 0,1368
| 0,59
| 0,2224
| 0,83
| 0,2967
| | 0,12
| 0,0478
| 0,36
| 0,1406
| 0,60
| 0,2257
| 0,84
| 0,2995
| | 0,13
| 0,0517
| 0,37
| 0,1443
| 0,61
| 0,2291
| 0,85
| 0,3023
| | 0,14
| 0,0557
| 0,38
| 0,1480
| 0,62
| 0,2324
| 0,86
| 0,3051
| | 0,15
| 0,0596
| 0,39
| 0,1517
| 0,63
| 0,2357
| 0,87
| 0,3078
| | 0,16
| 0,0636
| 0,40
| 0,1554
| 0,64
| 0,2389
| 0,88
| 0,3106
| | 0,17
| 0,0675
| 0,41
| 0,1591
*
| 0,65
| 0,2422
| 0,89
| 0,3133
| | 0,18
| 0,0714
| 0,42
| 0,1628
| 0,66
| 0,2454
| 0,90
| 0,3159
| | 0,19
| 0,0753
| 0,43
| 0,1664
| 0,67
| 0,2486
| 0,91
| 0,3186
| | 0,20
| 0,0793
| 0,44
| 0,1700
| 0,68
| 0,2517
| 0,92
| 0,3212
| | 0,21
| 0,0832
| 0,45
| 0,1736
| 0,69
| 0,2549
| 0,93
| 0,3238
| | 0,22
| 0,0871
| 0,46
| 0,1772
| 0,70
| 0,2580
| 0,94
| 0,3264
| | 0,23
| 0,0910
| 0,47
| 0,1808
| 0,71
| 0,2611
| 0,95
| 0,3289
|
| x
| Ф(x)
| x
| Ф(x)
| x
| Ф(x)
| x
| Ф(x)
|  0,96 0,96
| 0,3315
| 1,37
| 0,4147
| 1,78
| 0,4525
| 2,36
| 0,4909
| | 0,97
| 0,3340
| 1,38
| 0,4162
| 1,79
| 0,4633
| 2,38
| 0,4913
| | 0,98
| 0,3365
| 1,39
| 0,4177
| 1,80
| 0,4641
| 2,40
| 0,4918
| | 0,99
| 0,3389
| 1,40
| 0,4192
| 1,81
| 0,4649
| 2,42
| 0,4922
| | 1,00
| 0,3413
| 1,41
| 0,4207
| 1,82
| 0,4656
| 2,44
| 0,4927
| | 1,01
| 0,3438
| 1,42
| 0,4222
| 1,83
| 0,4664
| 2,46
| 0,4931
| | 1,02
| 0,3461
| 1,43
| 0,4236
| 1,84
| 0,4671
| 2,48
| 0,4934
| | 1,03
| 0.3485
| 1,44
| 0,4251
| 1,85
| 0,4678
| 2,50
| 0.4938
| | 1,04
| 0,3508
| 1,45
| 0,4265
| 1,86
| 0,4686
| 2,52
| 0,4941
| | 1,05
| 0,3531
| 1,46
| 0,4279
| 1,87
| 0,4693
| 2,54
| 0,4945
| | 1,06
| 0,3554
| 1,47
| 0,4292
| 1,88
| 0,4699
| 2,56
| 0,4948
| | 1,07
| 0,3577
| 1,48
| 0,4306
| 1,89
| 0,4706
| 2,58
| 0,4951
| | 1,08
| 0,3599
| 1,49
| 0,4319
| 1,90
| 0,4713
| 2,60
| 0,4953
| | 1,09
| 0,3621
| 1,50
| 0,4332
| 1,91
| 0,4719
| 2,62
| 0,4956
| | 1,10
| 0,3643
| 1,51
| 0,4345
| 1,92
| 0,4726
| 2,64
| 0,4959
| | 1,11
| 0,3665
| 1,52
| 0,4357
| 1,93
| 0,4732
| 2,66
| 0,4961
| | 1,12
| 0,3686
| 1,53
| 0,4370
| 1,94
| 0,4738
| 2,68
| 0,4963
| | 1,13
| 0,3708
| 1,54
| 0,4382
| 1,95
| 0,4744
| 2,70
| 0,4965
| | 1,14
| 0,3729
| 1,55
| 0,4394
| 1,96
| 0,4750
| 2,72
| 0,4967
| | 1,15
| 0,3749
| 1,56
| 0,4408
| 1,97
| 0,4756
| 2,74
| 0,4969
| | 1,16
| 0,3770
| 1,57
| 0,4418
| 1,98
| 0,4761
| 2,76
| 0,4971
| | 1,17
| 0,3790
| 1,58
| 0,4429
| 1,99
| 0,4767
| 2,78
| 0,4973
| | 1,18
| 0.3810
| 1,59
| 0,4441
| 2,00
| 0,4772
| 2,80
| 0,4974
| | 1,19
| 0.3830
| 1,60
| 0,4452
| 2,02
| 0,4783
| 2,82
| 0,4976
| | 1,20
| 0,3849
| 1,61
| 0,4463
| 2,04
| 0,4793
| 2,84
| 0,4977
| | 1,21
| 0,3869
| 1,62
| 0,4474
| 2,06
| 0,4803
| 2,86
| 0,4979
| | 1,22
| 0,3883
| 1,63
| 0,4484
| 2,08
| 0,4812
| 2,88
| 0,4980
| | 1,23
| 0,3907
| 1,64
| 0,4495
| 2,10
| 0,4821
| 2,90
| 0,4981
| | 1,24
| 0,3925
| 1,65
| 0,4505
| 2,12
| 0,4830
| 2,92
| 0,4982
| | 1,25
| 0,3944
| 1,66
| 0,4515
| 2,14
| 0,4838
| 2,94
| 0,4984
| | 1,26
| 0,3962
| 1,67
| 0,4525
| 2,16
| 0,4846
| 2,96
| 0,4985
| | 1,27
| 0,3980
| 1,68
| 0,4535
| 2,18
| 0,4854
| 2,98
| 0,4986
| | 1,28
| 0,3997
| 1,69
| 0,4545
| 2,20
| 0,4861
| 3,00
| 0,4987
| | 1,29
| 0,4015
| 1,70
| 0,4554
| 2 22
| 0,4868
| 3,20
| 0,4993
| | 1,30
| 0,4032
| 1,71
| 0,4564
| 2,24
| 0,4875
| 3,40
| 0,4997
| | 1,31
| 0,4049
| 1,72
| 0,4573
| 2,26
| 0,4881
| 3,60
| 0,4998
| | 1,32
| 0,4066
| 1,73
| 0,4582
| 2,28
| 0,4887
| 3,80
| 0,4999
| | 1,33
| 0,4082
| 1,74
| 0,4591
| 2,30
| 0,4893
| 4,00
| 0,5000
| | 1,34
| 0,4099
| 1,75
| 0,4599
| 2,32
| 0,4898
|
|
| | 1,35
| 0,4115
| 1,76
| 0,4608
| 2,34
| 0,4904
|
|
| | 1,36
| 0,4131
| 1,77
| 0,4616
|
|
|
|
|
Закінчення додатку 5
Додаток 6
Таблиця критичних точок 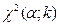 розподілу Пірсона розподілу Пірсона 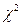 ( (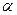 − рівень значущості; − рівень значущості;  −число степенів вільності) −число степенів вільності)
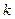
| 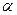
|
0,01
| 0,025
| 0,05
| 0,95
| 0,975
| 0,89
| |
| 6,6
| 5,0
| 3,8
| 0,0039
| 0,00098
| 0,00016
| |
| 9,2
| 7,4
| 6,0
| 0,103
| 0,051
| 0,020
| |
| 11,3
| 9,4
| 7,8
| 0,352
| 0,216
| 0,115
| |
| 13,3
| 11,1
| 9,5
| 0,711
| 0,484
| 0,297
| |
| 15,1
| 12.8
| 11,1
| 1,15
| 0,831
| 0,554
| |
| 16,8
| 14,4
| 12,6
| 1,64
| 1,24
| 0,872
| |
| 18,5
| 16,0
| 14,1
| 2,17
| 1,69
| 1,24
| |
| 20,1
| 17,5
| 15,5
| 2,73
| 2,18
| 1,65
| |
| 21,7
| 19,0
| 16,9
| 3,33
| 2,70
| 2,09
| |
| 23,2
| 20,5
| 18,3
| 3,94
| 3,25
| 2,56
| |
| 24,7
| 21,9
| 19,7
| 4,57
| 3,82
| 3,05
| |
| 26,2
| 23,3
| 21,0
| 5,23
| 4,40
| 3,57
| |
| 27,7
| 24,7
| 22,4
| 5,89
| 5,01
| 4,11
| |
| 29,1
| 26,1
| 23,7
| 6,57
| 5,63
| 4,66
| |
| 30,6
| 27,5
| 25,0
| 7,26
| 6,26
| 5,23
| |
| 32,0
| 28,8
| 26,3
| 7,96
| 6,91
| 5,81
| |
| 33,4
| 30,2
| 27,6
| 8,67
| 7,56
| 6,41
| |
| 34,8
| 31,5
| 28,9
| 9,39
| 8,23
| 7,01
| |
| 36,2
| 32,9
| 30,1
| 10,1
| 8,91
| 7,63
| |
| 37,6
| 34,2
| 31,4
| 10,9
| 9,59
| 8,26
| |
| 38,9
| 35,5
| 32,7
| 11,6
| 10,3
| 8,90
| |
| 40,3
| 36,8
| 33,9
| 12,3
| 11,0
| 9,54
| |
| 41,6
| 38,1
| 35,2
| 13,1
| 11,7
| 10,2
| |
| 43,0
| 39,4
| 36,4
| 13,8
| 12,4
| 10,9
| |
| 44,3
| 40,6
| 37,7
| 14,6
| 13,1
| 11,5
| |
| 45,6
| 41,9
| 38,9
| 15,4
| 13,8
| 12,2
| |
| 47,0
| 43,2
| 40,1
| 16,2
| 14,6
| 12,9
| |
| 48,3
| 44,5
| 41,3
| 16,9
| 15,3
| 13,6
| |
| 49,6
| 45,7
| 42,6
| 17,7
| 16,0
| 14,3
| |
| 50,9
| 47,0
| 43,8
| 18,5
| 16,8
| 15,0
|
Література
1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1998.
2. Ковтун Н.В., Столяров Г.С. Загальна теорія статистики: Курс лекцій. – К.: Четверта хвиля, 1996.
3. Харченко Л.П. и др. Статистика: Учебное пособие / Под ред. В.Г. Ионина. – Изд. 2-е. – М., 2002.
4. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. – М., 2004.
5. Теория статистики: Учебник / Под ред. Г.Л. Громыко. – М., 2002.
6. Теория статистики: Учебник / Р.А. Шмойлова и др.; под ред. Р.А. Шмойловой. – М., 2003.
7. Практикум по теории статистики: Учебное пособие / Р.А. Шмойлова и др.; под ред. Р.А. Шмойловой. – М., 2004.
8. Мармоза А.Т. Теорія статистики. – К., 2003.
9. Октябрьский П.Я. Статистика: Учебник. – М., 2003.
10. Мармоза А.Т. Практикум з теорії статистики. – К., 2003.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|




