Если уравнение имеет целый корень, то он является делителем числа

-1, т.е. равен 1 или -1. Проверка показывает, что х₁=-1.

По формулам Виета имеем: х₁*х₂=- ® х₂= .

Ответ:{-1; }

Пример 6

При каких значениях параметра «а» число является корнем уравнения х⁴-2х²+3а=0?

Решение:

Пусть х²=t®t²-2t+3a=0. По формулам Виета:

Если х= корень уравнения, то t₁=x²=2- ®t₂=2-t₁®

®a= -1.

Ответ: a= -1.

Следующие примеры решите самостоятельно.

Пример 7

Найти все натуральные решения неравенств:

1) –х⁴+8х²+9> 0;

2) < 0.

Ответ: 1){1;2}; 2) {1;2}

Пример 8

Дано: A={xÎN| x²-7x-8≤ 0}; B={xÎZ| ≤3}

Найти: 1) С=А 2)D=A .

Ответ: С={-3;-2;-1;0;1;2;3;4;5;6;7;8}; D={1;2;3;4;5;6}.

Пример 9

Дано: A={xÎZ | ≤ 0}; B={xÎN| }.

Найти: 1) С=А 2)D=A .

Ответ: С={-1;0;1;7;8;9;10}; D={-1;1}

Пример 10

Если двузначное число разделить на сумму его цифр, то получится в частном 4 и в остатке 3. Если это число разделить на произведение его цифр, то получится в частном 3 и в остатке 5.

Найдите это двузначное число.

Ответ: 23

Пример 11

Решить уравнения:

1) 2002х²-2001х-1=0;

57х²-101х-26=0.

Ответ:1) {1;- };2) {2;- }.

Пример 12

При каких значениях параметра «а» число является корнем уравнения: х⁴-6х²+4а²=0?

Ответ:а=-1;а=1.

ГЛАВА 2. Модуль вещественного числа. Решение уравнений и неравенств со знаком модуля.

Простейшие уравнения со знаком модуля.

1. |f(x)|=a®

2. | f(x) | =g(x) «

3. |f(x)|=|g(x)|«

частный случай:|х-а|=|х-в| «х=

4. |f(x)|+|g(x)|=0 «

Пример 1

Решить уравнения:

1) |5-3х|=2; 2) |х²-13х+40|=0; 3) |4-х²|=-2.

Решение:

1) |5-3х|=2« «

Ответ:{1; }

2) | х²-13х+40 | =0 «х²-13х+40=0 «

Ответ:{5;8}

3) | 4-х² | =-2 « Ответ:

Пример 2

Решить уравнения:

1) |х²-5х-6|=2х-12; 2) |х²-3х-10|=2х+14; 3) |х²-25|=-30-6х;

4) |х²-7х+18|=2х-2; 5) |х²+5х+13|=-2х+1.

Решения:

1) |х²-5х-6|=2х-12 О.Д.З. 2х-12³0«х³6

Заметим, что х²-5х-6³0 при х³6, т.к. х²-5х-6=(х-6)*(х+1)

|х²-5х-6|= х²-5х-6® х²-5х-6=2х-12 «х²-7х+6=0 «

Ответ: {6}

2) | х²-3х-10 | =2х+14 « «

«

Ответ:{-5;8}

3) |х²-25|=-30-6х О.Д.З. -30-6х³0«х≤-5

|х²-25|= х²-25 ® х²-25=-30-6х «х²+6х+5=0 « Ответ: {-5}

4) |х²-7х+18|=2х-2 « «

«

Ответ: {4;5}

5) | х²+5х+13 | =-2х+1 « « «

Ответ: {3;4}

Пример 3

Решить уравнения:

1) |2х²+3х+5|=|2х²+3х-3|; 2) |х³+х-1|=|х³+х+5|; 3) |х²-4х+8|=|х²-14|;

4)|х³-27|+|х²-4х+3|=0; 5) | -1|+|х⁴-5х²+4|=0

Решения:

1) | 2х²+3х+5 | = | 2х²+3х-3 |; пусть 2х²+3х=t ®| t+5 | = | t-3 |«t= =-1 ®

2х²+3х=-1«

Ответ: {-0,5; -1}

2) | х³+х-1 | = | х³+х+5 |; пусть х³+х=t ®| t-1 | = | t+5 |«t= =-2 ®

х³+х=-2«х³+х+2=0 «(x³+1)+(x+1)=0«(x+1)(x²-x+2)=0 «x=-1

(x²-x+2

Ответ: {-1}

3) | х²-4х+8 | = | х²-14 |« « «

«

Ответ: {-1;3;5,5}

4)|х³-27|+|х²-4х+3|=0 « « «x=3

Ответ: {3}

5) | -1|+|х⁴-5х²+4|=0 « « « «x=2

Ответ: {2}

Пример 4

Решить уравнение:

|х-3|-|2х+1|=х-4

Решение:

|х-3|-|2х+1|=х-4

« Ответ:{1,5}

Пример 5

Решить уравнения (самостоятельно)

1) |7+12х|=4; 2) |х⁴-27х|=0; 3) |5-х³+х|=-1

Ответ:1){- ; }; 2) {0;3}; 3) .

Пример 6

Решить уравнения (самостоятельно)

1) |х²-7х+6|=х-6; 2) |х²-10х+2|=-5х+54; 3) |49-х²|=-3х-21;

4) |х²-4х+3|=2х+10; 5) |х²+9х+8|=4х+2.

Ответ: 1){6}; 2) {7;8; };3) {-7}; 4) {-1;7}; 6)

Пример 7

Решить уравнения (самостоятельно)

1) |4х²-6х-1|=|4х²-6х-7|; 2) |2х³-х|=|2х³-х-2|; 3)|х²+2х+10|=|х²-50|;

4)|х³+125|+|х²+4х-5|=0; 5) | -1|+|х⁴-10х²+9|=0.

Ответ: 1){-0,5;2}; 2) {1}; 3) {-30;-5;4}; 4) {-5};5){-1}

Пример 8

Решить уравнение (самостоятельно)

|3х+1|-|х+2|=4-2х.

Ответ: { }

Простейшие неравенства со знаком модуля.

1.

2.

Ответ: xÎ[x₀-a;x₀+a]

3.

Ответ: xÎ(

4.

Ответ: xÎ -a] [x₀+a;+

5. |f(x)|≤a (a>0) «

6. |f(x)|³a (a>0) «

7. ³0 «f(x)>0

8. ≤0 «f(x)<0

9.

10. |f(x)|³g(x) «

11. |f(x)|³|g(x)| « «(f(x)-g(x))*(f(x)+g(x))³0

12. |f(x)|≤|g(x)| « «(f(x)-g(x))*(f(x)+g(x))≤0

Пример 1

Решить следующие неравенства:

1) |3х-15|>10; 2) |7х+12|≤5; 3) |7-5х|³7; 4) |4-3х|≤4; 5) ³0;

≤0; 7) ≤0; 8) >0.

1)

Ответ: хÎ(- ;5/3)

2)

Ответ: хÎ[- ;-1]

3)

Ответ:хÎ

4)

Ответ: хÎ[0;8/3]

5) ³ 0 « «

Ответ: хÎ

≤0 « «

Ответ: хÎ(

6) ≤0 « «

Ответ:

8) >0 « «

Ответ: хÎ(

Пример 2

Решить следующие неравенства:(самостоятельно)

1) |5х-2|³ 10; 2) |4-3х|<12; 3) |2х+10|>1; 4) |10х+1|≤20; 5) ³0;

6) ≤0; 7) <0; 8) ³0.

Ответы: 1)

4) [-2,1;1,9]; 5) (

7) ; 8)

Пример 3

Решить следующие неравенства:

1) |х²+25|≤10х; 2) |х²+6х+10|³5; 3) |х+8|≤х²+6; 4) |х²-4|³2х-5;

5) |х²-5х|<3х-7; 6) |х²-6|≤|х²+4х|; 7) |2х+5|>|х²-4х-2|;

8) |х²+5х+9|≤|х²-7х-4|

Решения:

1) | х²+25 | ≤10х(т.к. х²+25>0, то | х²+25 | =х²+25) «х²+25≤ 10х «

«х²-10х+25≤0 «(х-5)²≤0 «х=5

Ответ: {5}

2) | х²+6х+10 |³ 5 (т.к. х²+6х+10>0 /дискриминант отрицательный/,то

|х²+6х+10|=х²+6х+10) «х²+6х+10³5 «х²+6х+5³0 «(х+5)*(х+1)³0

Ответ: хÎ ]

3) | х+8 | ≤х²+6 (x²+6>0) « « «

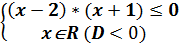
Ответ: хÎ[-1;2]

4) | х²-4 |³ 2х-5 « « «

«

Ответ: хÎ

5) | х²-5х |< 3х-7 « « «

«

3.8

Ответ: хÎ(1+ 7)

6) | х²-6 | ≤ | х²+4х |«6) (х²-6)²≤(х²+4х)² «(х²-6)²-(х²+4х)²≤0 «

Ответ: xÎ[-3;-3/2]

7) | 2х+5 | > | х²-4х-2 |«(2х+5)²>(х²-4х-2)² «(2х+5)²-(х²-4х-2)²>0 «

Ответ: хÎ(1;7)

8) |х²+5х+9|≤|х²-7х-4| Заметим. что х²+5х+9>0 т.к. D<0 ®

| х²+5х+9 | =х²+5х+9®|x²-7x-4|³х²+5х+9 « « «x≤-

Ответ: хÎ (-

Пример 4

Решить следующие неравенства (самостоятельно):

1) |х²+81|³ -18х; 2) |х²-8х+14|≤2; 3) |2х+1|³х²+2; 4) |х²-10х+14|<2х+3;

5) |4х-13|³х²-9; 6) |х²-2х+2|³|6-х²|; 7) |х²-2х-3|>2|х-3|;

8) |х²-7х+2|≤|х²-7х+10|.

Ответы: 1) (-∞;+∞); 2) [2;6]; 3) {1}; 4) (1;11); 5)[-2- ;-2+ ];

6) (- ;-1] ; 8)

Пример 5

Решить следующие неравенства:

1) |х-1|-|2х+5|³3х-4;

2) |2х+1|+|4-2х|≤6х+1.

Решения:

1)

2)

«

Ответ: хÎ[2/3;+∞)

Пример 6

Решить следующие неравенства (самостоятельно)

1) |3х+1|-|2х-3|≤х+5;

2) |4х-8|+|4х+12|³5-4х.

Ответы: 1)[ -4,5;+∞); 2) (-∞;+∞).

Пример 7

Решить следующие неравенства:

1) ≤0; 2) | ³-11; 3) | ≤1; 4) ≤0

Решение:

1) ≤0 « ≤0 « «

Ответ: хÎ(-1/3; 1/3)

2) | ³ -11 « «

Ответ: хÎ[-5/3;-1)

3) | ≤1 (x²+4>0) « « «

Ответ: xÎ(-

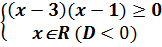
4) ≤0 « ≤0 «x+3 < 0 «x < -3,

Ответ: хÎ(-∞;-3)

Пример 8

Решить следующие неравенства (самостоятельно)

1) ³0; 2) | ; 3) | |³2; 4) .

Ответ: 1) хÎ :

3) xÎ .

Пример 9

Решить системы неравенств:

1) ; 2) .

Решение:

1)

-3

х

-2

х

-3

х

 

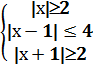
Ответ: xÎ[2;5]

2)

1,5

x

x

-2,5

«

«

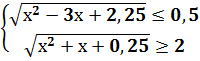Ответ: xÎ[1,5;2]

Пример 10

Решить системы неравенств (самостоятельно):

1) ; 2) .

Ответ: 1) xÎ[2;4] ; 2){1,6}

ГЛАВА 3. Элементы теории множеств.

§1 Основные понятия.

Напомним, что универсальное множество, которое содержит в себе все другие множества, обозначается буквой W.

Пустое множество обозначается .

А

A «{x| (xÎA)Ù((xÎB)}

A\B (разность множеств) «{x| (xÎA)Ù(x B)}

=W\A (дополнение множества А до W)

При работе с множествами будем использовать следующие свойства основных операций над множествами.

N	Объединение	Пересечение
	А	А
	(А	(А В)
	А
	А=W	А

Первый дистрибутивный закон:

Второй дистрибутивный закон

N	Свойства дополнения
	=W

⇐ Предыдущая12345678910Следующая ⇒

Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом...

Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...

ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования...

Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все...

---

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: