|
|
Примечание: формулы 6 и 7 называют формулами де Моргана
Решение примеров. Пример 1. Дано: АÌВÌСÌD Упростить: а) ( b) ( c) Решение:
а) ( Ответ: B b) ( Заметим, что Ответ: c) Ответ: Пример 2 Дано: AÌB; CÌD; Упростить: a) b) c) d) Решение:
a) Ответ: в) Ответ: С с) Ответ: d) Ответ: D Пример 3 Упростить:

Решение:
Ответ: А Пример 4 Упростить:
Решение:
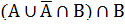 =( =( 
Ответ: В Пример 5 Упростить:
Решение:
Ответ: Пример 6 Упростить:

Решение:
Ответ: А Пример 7 Дано: A={xÎR| |x-2|³2}; B={xÎR| |x|≤4}; C={xÎR| |x+1|≤5} Найти: a) Решение:
А=
B=[-4;4]
C=[-6;4] Ответ: a) b) c) Пример 8 Дано: A={xÎR| Найти: а) Решение: A={xÎR|
A=[-0,5;1,5]
B={xÎR|
B= Ответ: a) ;c)A\B=[-0,5;0] Пример 9 (самостоятельно) Дано: Упростить: a) b) c) ( d) e) Ответ: a) A; b) D; c) Пример 10. (самостоятельно) Дано: AÌBÌC; C∩D=∅ Упростить: a) (A∪B∪C)∩ b) (A∩C)∪B∩D c) ( Ответ: a) C; b)C; c) B∪D. Пример 11 (самостоятельно) Упростить: (А∪(А∩В))∩(А∩В). Ответ:А∩В Пример 12 (самостоятельно) Упростить: (А∩В)∪(А∩ Ответ: А Пример 13 (самостоятельно) Упростить: (А∩ Ответ: А Пример 14 (самостоятельно) Упростить: А∩(А∪А∩В)∪В∩( Ответ: В Пример 15 (самостоятельно) Дано: A={x∈R| |x+0,5|≤2,5}; B={xÎR| |x-0,5|³0,5}; C={xÎR| |x+0,4|≤2,6} Найти: a) A∪B∪C; b)A∩B∩C; c)(A∪C)∩B Ответ: a) R; b)[-3;1]∪{2}; c) [-3;1]∪[2;2,2] Пример 16 (самостоятельно) Дано: A={xÎR| B={xÎR| Найти: a) A∪B; b)A∩B; c)A\B. Ответ: a) (-∞;-1,6]∪[11/3;+∞);b) [-2,4;-7/3];c) (-7/3;1,6] Пример 17 Дано: A={xÎR| |4x2+1|≤4x}; B={xÎR| |x+3|-|2x+1|≤x+4} Найти:a)C=A∪B; b)D=A∩B; c)E= Решение: |4x2+1|≤4x «4x2+1≤4x «4x2+1-4x≤0 «(2х-1)2≤0«
|x+3|-|2x+1|≤x+4
B=R Ответ: a)C=R; b)D=A={0,5}; c)E=∅ Пример 18 Дано: A={xÎR| |6x2-14x+18,8|-x2-9=0}; B={xÎR| Найти: А∪В. Решение: |6x2-14x+18,8|-x2-9=0 « « A={1,4}
B=(-∞;-0,2]∪[0,2;√3/2)∪(√3/2;+∞) Ответ: А∪В=В==(-∞;-0,2]∪[0,2;√3/2)∪(√3/2;+∞) Пример 19 (самостоятельно) Дано: A={xÎR| |4x2+5x-8|-|4x2+5x+6|=0} B={xÎR| | Найти: А∪В. Ответ: (2;3)∪(3;+∞)∪{-0,25}∪{-1} Пример 20 (самостоятельно) Дано: A={xÎR| |x2-x+4|-|x2-x-8|≤0}; B={xÎR| Найти: А∩В. Ответ: [-1;0,5) Пример 21 (самостоятельно) Дано: A={xÎR| Найти: А∪В. Ответ: (-∞;-5)∪{2/3}∪[1;+∞). Пример 22 (самостоятельно) Дано: A={xÎR| |x2-4x+8|-|x2-14|=0}; B={xÎR| |x4+x|+|x3-8x2-9x|=0} Найти: а) А∪В; b) А∩В. Ответ: а) {-1;0;3;5,5} b){-1} ГЛАВА 4. Отображение множеств. Виды отображений. Основные понятия и определения. Если даны два множества А и В, то можно различными способами установить соответствие между этими множествами. Но только, если каждому элементу множества А по некоторому правилу f ставится в соответствие определённый элемент множества В, то говорят, что задано отображение множества А в множество В.
Обозначения: f: A® B; (A® B) (А, В. f) А- область определения отображения f. Если элемент b (bÎB)получен из элемента а (аÎА), то b_-образ элемента а. В свою очередь. а=f-1(b)- прообраз элемента b. Множество всех образов: f(A)={bÎB| b=f(a), aÎA} Различают следующие виды отображений: 1.Сюръекция. Если f(A)=B, т.е.каждый элемент из множества В является образом некоторого элемента а из множества А, то отображение называют сюръективным или сюръекцией или говорят: отображение множества А на множество В. Инъекция. Если из условия а1≠а2 ® f(a1)≠f(a2), т.е. разным образам соответствуют разные прообразы, то отображение называют инъективным или инъекцией (предполагается, что не обязательно выполнение условия f(A)=B). Биекция Если выполнены два условия:
 , то говорят, что отображение между множествами А и В является биективным или биекцией или взаимно однозначным соответствием. , то говорят, что отображение между множествами А и В является биективным или биекцией или взаимно однозначным соответствием.
A «B Различие между видами отображений показаны на следующих рисунках. Отображение множества А в множество В (общий случай).
Сюръекция (отображение множества А на множество В)
Инъекция.
Биекция (взаимно однозначное соответствие)
Заметим, что если множества А и В конечные, то число элементов множества А равно числу элементов множества В. Тождественное отображение I из множества А в множество А означает: ∀аÎА ®I(а)=а
Произведением (композицией) отображений f и g называется отображение, обозначаемое g*f: A®C, которое задано на множестве А, и при этом справедлива формула: g*f(a)=g(f(a))=g(b)=c [Заметим. что g*f≠f*g] Обратное отображение. Обозначим f: A®B; f-1: B®A.
f-1- обратное отображение для f, если:
f*f-1(b)=f(f-1(b))=f(a)=b. f-1*f(a)=f-1(f(a))=f-1(b)=a.   Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...  Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...  ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала...  ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|