ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА

В. М. Метельский

Ю. В. Минченков

М. И. Овсеец

Е. М. Светлая

ВЫСШАЯ МАТЕМАТИКА

ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА

Учебно-методическое пособие

УДК 51

ББК 22.1

М 54

Рекомендовано к изданию редакционно-издательским советом
Частного института управления и предпринимательства

А в т о р ы:

доцент кафедры высшей математики и статистики

Частного института управления и предпринимательства

кандидат физико-математических наук В. М. Метельский;

Метельский, В. М.

М 54 Высшая математика. Основы математического анализа: учеб. – метод. пособие / В.М. Метельский [и др.]. – Минск: Частн. ин-т упр. и предпр., 2010. – 115 с.

ISBN 978-985-6971-08-5.

Подготовлено в соответствии с рабочей программой ЧИУиП данной дисциплины, стандартом и типовой программой Минобразования Республики Беларусь. Содержит лекции по математическому анализу и дифференциальным уравнениям.

Предназначено для студентов Частного института управления и предпринимательства.

УДК 51

ББК 22.1

© Метельский В.М., Минченков Ю.В., Овсеец М.И., Светлая Е.М., 2010

ISBN 978-985-6971-08-5 © Частный институт управления и предпринимательства, 2010

План

1 Понятие числовой последовательности. Предел числовой последовательности. Свойства сходящихся числовых последовательностей.

2 Бесконечно большие и бесконечно малые числовые последовательности. Основные способы вычисления пределов.

Ключевые понятия

Бесконечная числовая последовательность.

Предел бесконечной числовой последовательности.

Бесконечно большие числовые последовательности.

Бесконечно малые числовые последовательности.

Монотонные последовательности.

Второй замечательный предел.

1 Понятие числовой последовательности.
Предел числовой последовательности.

Свойства сходящихся последовательностей

1 Сходящаяся последовательность имеет единственный предел.

2 Сходящаяся последовательность ограничена.

3 Если , то, начиная с некоторого номера N, члены последовательности имеют тот же знак, что и знак а.

4 .

5 Если последовательности и сходятся и то:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

Бесконечно большие и бесконечно малые числовые последовательности. Основные способы вычисления пределов

Определение 7 Последовательность называется бесконечно большой последовательностью (б.б.п.), если для любого числа e существует номер , такой, что для всех выполняется неравенство . В этом случае употребляют специальный символ ¥ и пишут . (Если х_n >e, то . Если х_n < e, то ).

Определение 8 Последовательность называется бесконечно малой последовательностью (б.м.п.), если .

Заметим, что никакая постоянная последовательность не является бесконечно большой, в то же время только одна постоянная последовательность – нулевая является бесконечно малой последовательностью.

Предел функции в точке. Односторонние пределы.

Бесконечно малые и бесконечно большие функции.

Замечательные пределы

Определение 5 Функция называется бесконечно малой функцией (б.м.ф.) при , если

Определение 6 Функция называется бесконечно большой функцией (б.б.ф.) при , если для любого числа e можно указать такое число что для всех х, удовлетворяющих условию

, выполняется неравенство .

В этом случае употребляют специальный символ ¥ и пишут . (Если , то . Если , то ).

Пример 4:

а) функция б.м.ф. при ;

б) функция б.б.ф. при

Таблица основных производных

1) с' = 0, с R;

2) х ' =1;

3) (х^α)' = αx^α-1, α R;

4) (а^х)' = а^х ln а, 0 < a ¹ 1;

5) (e^x)' = e^x;

6) 0 < a ¹ 1, х > 0;

7) х > 0;

8) (sin x)' = cos x;

9) (cos x)' = – sin x;

10) Z;

11) Z;

12) ;

13) ;

14) ;

15) .

Пример 3 Найти уравнения касательной и нормали к графику функции f (x)= 3 х ² + 4 в точке х ₀ = 2.

Решение. Найдем производную функции f (x): f¢ (x) = 6 х.

Для того чтобы составить уравнения касательной и нормали (5) и (6), необходимо найти значения функции и ее производной в точке х ₀ = 2:

f (2) = 3 × 2² + 4 = 16;

f ' (2) = 6 × 2 = 12.

Следовательно, уравнение касательной имеет вид:

у = 12 (х – 2) + 16,

уравнение нормали:

Ответ: у = 12 (х – 2) + 16,

Пример 4 Найти производные функций.

а) ;

б) ;

в) ;

г) .

Решение

а) ;

б) ;

в) ;

г)

(вначале взяли производную степенной функции, затем производную sin 8 x, а в конце производную 8 х).

ДИФФЕРЕНЦИАЛ ФУНКЦИИ

План

1 Раскрытие неопределенностей при помощи правила Лопиталя.

2 Дифференциал функции, его геометрический смысл. Применение дифференциала в приближенных вычислениях.

Ключевые понятия

Правило Лопиталя.

Дифференциал функции.

Раскрытие неопределенностей.

Пример 2

а)

;

б)

.

2 Дифференциал функции, его геометрический смысл.
Применение дифференциала в приближенных вычислениях

Определение 1 Функция f (х) называется дифференцируемой в точке х ₀, если ее приращение в этой точке можно представить в виде

(1)

где А R, a(Δ х) – бесконечно малая функция более высокого порядка малости, чем Δ х при Δ х → 0, т.е. .

Теорема: для того, чтобы функция f (x) была дифференцируемой
в точке х ₀, необходимо и достаточно, чтобы в точке х ₀ существовала производная f¢ (x ₀) = А.

Следовательно, из формулы (1) имеем

. (2)

Определение 2 Функция (от D х) есть главная линейная часть приращения функции f (x) в точке х ₀. Эту главную линейную часть приращения функции f (x) и называют дифференциалом функции f (x) в точке х ₀ и обозначают

(3)

В частности, для f (x) = х имеем

Следовательно, из формулы (3) получаем:

. (4)

Выясним геометрический смысл дифференциала (см. рисунок):

ВД = ВС + СД; ВД = ВС = Ð А =
= , так как АВ = , Ð А = .

Следовательно, из уравнения (2) имеем СД = α().

Таким образом, ВС =

Следовательно, с геометрической точки зрения, дифференциал функции равен приращению ординаты касательной, проведенной к графику функции в точке с абсциссой х ₀, при приращении аргумента .

Для дифференциалов функций f и g справедливы формулы, подобные формулам для производных функций:

1) ;

2) ;

3)

Пример 3 Найти дифференциалы функций:

а) ;

б) ;

в) ;

г) ;

д) .

Заметим, что dx = d (x + c), с R, d (ax + в) = adx Þ dx =

Данные формулы будут широко применяться при вычислении интегралов функций. С помощью дифференциала можно также приближенно вычислить значения функции f для х, близких к х ₀. Так, отбросив бесконечно малую функцию в формуле (2), получаем

. (5)

Пример 4 Вычислить приближенно:

а) ; б) .

Решение. Воспользуемся формулой (5):

а) ;

х ₀ = 64, = 0,05;

Следовательно,

Заметим, что ;

б)

Þ

Заметим, что

Лекция 5 ИССЛЕДОВАНИЕ ФУНКЦИЙ

План

1 Локальные экстремумы функции. Достаточные условия экстремума функции.

2 Исследование функций на выпуклость и вогнутость. Точка перегиба.

3 Асимптоты графика функции.

4 Общая схема построения графика функции.

Ключевые понятия

1 Локальные экстремумы функции.
Достаточные условия экстремума функции

Пусть задана функция у = f (х) на множестве Х и х ₀ – внутренняя точка множества Х.

Обозначим через U (х ₀) окрестность точки х ₀. В точке х ₀ функция f (х) имеет локальный максимум, если существует такая окрестность U (х ₀) точки х ₀, что для всех х из этой окрестности выполнено условие f (х) £ f (х ₀).

Аналогично: функция f (х) имеет в точке х ₀ локальный минимум, если существует такая окрестность U (х ₀) точки х ₀, что для всех х из этой окрестности выполнено условие f (х) ³ f (х ₀).

Определение 1 Точки локальных максимума и минимума называются точками локальных экстремумов, а значения функции в них – локальными экстремумами функции.

Пусть функция f (х) определена на отрезке [ а; b ] и имеет локальный экстремум на каком-то из концов этого отрезка. Тогда такой экстремум называется локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для точки а и левой для точки b полуокрестностью.

Проиллюстрируем данные выше определения:

На рисунке точки х ₁, х ₃ – точки локального минимума, х ₂, х ₄ – локального максимума, х = а – краевого максимума, х = b – краевого минимума.

Заметим, что наряду с локальными минимумом и максимумом определяют так называемые глобальные минимумы и максимумы функции f (х) на отрезке [ a; b ]. На рисунке точка х = а – точка глобального максимума
(в этой точке функция f (х) принимает наибольшее значение на отрезке
[ a; b ]), точка х = х ₃ – соответственно точка глобального минимума.

Из дифференцируемости функции f (x) в точке локального экстремума х ₀ следует, что f ' (x ₀) = 0. Данное условие является необходимым условием существования в точке локального экстремума, т. е. если в точке х ₀ – экстремум функции f (x) и в этой точке существует производная, то f ' (x ₀) = 0. Точки х ₀, в которых f ' (x ₀) = 0, называются стационарными точками функции. Заметим, что равенство нулю производной в точке не является достаточным условием для существования локального экстремума в этой точке.

Пример 1 у = х ³; у' = 3 х ²; у' (0) = 0, но
в точке х ₀ = 0 нет экстремума.

Определение 2 Критическими точками, т.е. точками, подозрительными на экстремум функции f (x) на интервале (a; b), являются точки, в которых производная существует и равна 0 либо она не существует или равна бесконечности. На рисунках функции имеют минимум в точке х ₀ = 0:

f '(0) = 0 f '(0) $ f '(0) = ¥

Рассмотрим достаточные условия существования в точке локального экстремума, которые позволят ответить на вопрос: «Есть ли в точке экстремум и какой именно – минимум или максимум».

Теорема 1 (первое достаточное условие экстремума). Пусть непрерывная функция f (x) дифференцируема в некоторой проколотой окрестности U (x ₀) точки х ₀. Тогда:

1) если (1)

то в точке х ₀ – локальный максимум;

2) если (2)

то в точке х ₀ – локальный минимум.

Пример 2 Исследовать на монотонность и локальный экстремум функцию с помощью производной первого порядка.

Решение. Найдем стационарные точки функции:

Þ х ² –1 = 0 Þ х ₁ = –1, х ₂ = 1.

Заметим, что данная функция не определена в точке х = 0. Следовательно:

х	(–¥; –1)	–1	(–1; 0)		(0; 1)		(1; +¥)
у'	+		–	–	–		+
у		–2		–

max min

То есть функция возрастает на интервалах (–¥; –1) и (1; +¥), убывает на интервалах (–1; 0), (0; 1), имеет локальный максимум в точке
х ₁ = –1, равный у _max (–1) = –2; имеет локальный минимум в точке х ₂ = 1,
у _min (1) = 2.

Определение 3 Функция называется n раз непрерывно-дифферен-цируемой на некотором промежутке, если на этом промежутке она имеет непрерывные производные до порядка n включительно (n = 0, 1, 2, …).

Теорема 2 (второе достаточное условие экстремума). Пусть функция f (x) дважды непрерывно-дифференцируема. Если х ₀ – стационарная точка
(f '(х ₀) = 0), в которой f ''(х ₀) > 0, то в точке х ₀ функция имеет локальный минимум. Если же f ''(х ₀) < 0, то в точке х ₀ функция имеет локальный максимум.

Пример 3 Исследовать на экстремум функцию с помощью второй производной.

Решение. В примере 2 для данной функции мы нашли первую производную и стационарные точки х ₁ = –1, х ₂ = 1.

Найдем вторую производную данной функции:

Далее найдем значения второй производной в стационарных точках:

Þ в точке х ₁ = –1 функция имеет локальный максимум;

Þ в точке х ₂ = 1 функция имеет локальный минимум (по теореме 2).

Заметим, что теорема 1 более универсальна. Теорема 2 позволяет проанализировать на экстремум лишь точки, в которых первая производная равна нулю, в то время как теорема 1 рассматривает три случая:
1) производная равна нулю; 2) производная не существует; 3) производная равна бесконечности в подозрительных на экстремум точках.

2 Исследование функций на выпуклость и вогнутость.
Точка перегиба

Пусть функция f (х) задана на интервале (a; b) и х ₁, х ₂ – любые различные точки этого интервала. Через точки А (х ₁; f (х ₁)) и В (х ₂; f (х ₂)) графика функции f (х) проведем прямую, отрезок АВ которой называется хордой. Уравнение этой прямой запишем в виде у = у (х).

Определение 4 Функция f (х) называется выпуклой вниз (вогнутой) на интервале (a; b), если для любых точек х ₁, х ₂ Î (a; b), а £ х ₁ < х ₂ £ b хорда АВ лежит не ниже графика этой функции, т. е. если f (х) £ у (х),

" х Î [ х ₁; х ₂] Ì (a; b):

Заметим, что выпуклую вниз функцию иногда называют вогнутой функцией. Аналогично определяется выпуклость функции вверх.

Определение 5 Функция f (х) называется выпуклой вверх (выпуклой) на интервале (a; b), если для любых точек х ₁, х ₂ Î (a; b), а £ х ₁ < х ₂ £ b хорда АВ лежит не выше графика этой функции, т. е. если f (х) ³ у (х),

" х Î [ х ₁; х ₂] Ì (a; b):

Теорема 3 (достаточное условие выпуклости). Если f (х) – дважды непрерывно дифференцируема на интервале (a, b) и:

1) f ''(х) > 0, " х Î (a; b), то на (a; b) функция f (х) выпукла вниз;

2) f ''(х) < 0, " х Î (a; b), то на (a; b) функция f (х) выпукла вверх.

Точка х ₀ называется точкой перегиба функции f (х), если $ d – окрест-ность точки х ₀, что для всех х Î (х ₀ – d, х ₀) график функции находится с одной стороны касательной, а для всех х Î (х ₀, х ₀ + d) – с другой стороны каса-тельной, проведенной к графику функции f (х) в точке х ₀, т. е. точка х ₀ – точка перегиба функции f (х), если при переходе через точку х ₀ функция f (х) меняет характер выпуклости:

х ₀ – d х ₀ х ₀ + d

Теорема 4 (необходимое условие существования точки перегиба). Если функция f (х) имеет непрерывную в точке х ₀ производную f '' и х ₀ – точка перегиба, то f '' (х ₀) = 0.

Теорема 5 (достаточное условие перегиба). Если функция f (х) дважды непрерывно дифференцируема в окрестности точки х ₀ и при переходе через точку х ₀ производная f ''(х) меняет знак, то точка х ₀ является точкой перегиба функции f (х).

Пример 4 Исследовать на выпуклость и найти точки перегиба функции у = х ³.

Решение: у' = 3 х ²; у'' = 6 х = 0 Þ х ₀ = 0 – точка, подозрительная на перегиб.

В точке х ₀ = 0 функция у = х ³ имеет перегиб:

Пример 5 Исследовать на выпуклость и найти точки перегиба функции .

Решение. В примере 3 мы уже находили вторую производную данной функции . Так как то точек, подозрительных на перегиб, нет. Рассмотрим промежутки выпуклости:

Асимптоты графика функции

Определение 6 Прямая х = х ₀ называется вертикальной асимптотой графика функции f (х), если хотя бы один из пределов f (х ₀–0) или f (х ₀ + 0) равен бесконечности.

Пример 6 Найти вертикальные асимптоты функций:

а) б) в)

Решение. В нашем случае вертикальными асимптотами функций будут прямые х = х ₀, где х ₀ – точка, в которой функция не определена:

а) х = 3 – вертикальная асимптота функции (действительно, );

б) х = 2, х = – 4 – вертикальные асимптоты функции (действительно, ;

);

в) х = 0 – вертикальная асимптота функции (действительно, ).

Определение 7 Прямая у = kx + b называется наклонной асимптотой графика непрерывной функции f (х) при х ® +¥ или х ® – ¥, если f (х) = kx + b + α(х), , т.е. если наклонная асимптота для графика функции f (х) существует, то разность ординат функции f (х) и прямой у = = kx + b в точке х стремится к 0 при х ® +¥ или при х ® – ¥.

Теорема 6 Для того чтобы прямая у = kx + b являлась наклонной асимптотой графика функции f (х) при х ® +¥ или х ® – ¥, необходимо и достаточно существование конечных пределов:

(3)

Следовательно, если хотя бы один из данных пределов не существует или равен бесконечности, то функция не имеет соответствующих наклонных асимптот.

Пример 7 Найти наклонные асимптоты функции

Решение. Найдем пределы (3). Пусть х ® +¥, тогда:

следовательно, k = 1;

следовательно, b = 0.

Таким образом, функция имеет наклонную асимптоту
у = kx + b = 1 х + 0 = х при х ® +¥. Аналогично можно показать, что прямая у = х будет наклонной асимптотой и при х ® – ¥.

Ответ: у = х – наклонная асимптота при х ® ± ¥.

Пример 8 Найти асимптоты функции .

Решение:

а) функция неопределена в точках х ₁ = –1, х ₂ = 1. Прямые х ₁ = –1, х ₂ = 1 – вертикальные асимптоты данной функции.

Действительно, ;

;

б) у = kx + b. Пусть х ® +¥, тогда:

Следовательно, у = 2 х + 1 – наклонная асимптота данной функции при х ® +¥. Эта же прямая будет наклонной асимптотой и при х ® – ¥.

Ответ: х ₁ = –1, х ₂ = 1 – вертикальные, у = 2 х + 1 – наклонная асимп-тоты.

Таблица основных неопределенных интегралов

Данную таблицу можно получить исходя из того, что интегрирование представляет собой операцию, противоположную дифференцированию. Часть формул этой таблицы непосредственно следует из таблицы производных основных элементарных функций. Справедливость остальных формул легко проверяется дифференцированием.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. , а ¹ 0.

13. , а ¹ 0.

14. .

15. , а ¹ 0.

16. , а ¹ 0.

Формула Ньютона-Лейбница

Теорема 2 Если функция непрерывна на отрезке и – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:

, (2)

которая называется формулой Ньютона-Лейбница.

Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа: на первом этапе находят некоторую первообразную для подынтегральной функции ; на втором –разность значений этой первообразной на концах отрезка .

Пример 1 Вычислить интеграл .

Решение. Для подынтегральной функции произвольная первообразная имеет вид . Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления интеграла возьмем первообразную, имеющую наиболее простой вид: . Тогда .

Пример 2 Вычислить интеграл .

Решение. По формуле Ньютона-Лейбница имеем:

.

Интегрирование по частям

Теорема 4 Пусть функции и имеют непрерывные производные на отрезке . Тогда имеет место следующая формула интегрирования по частям:

. (4)

Доказательство

Так как , то функция является первообразной для функции . Тогда по формуле Ньютона-Лейбница получаем:

,

откуда

.

Все рекомендации, данные выше для использования аналогичной формулы в неопределенном интеграле, имеют место и для формулы (4).

Пример 4 Вычислить .

Решение. Пусть , тогда . По формуле (4) находим:

.

Пример 5 Вычислить .

Решение. Пусть , тогда . Применяя формулу интегрирования по частям, получаем:

.

3 Вычисление площадей плоских фигур, объемов тел вращения,
длин дуг плоских кривых

Объем тела вращения

Пусть криволинейная трапеция, ограниченная графиком непрерывной на отрезке функции , осью , прямыми и , вращается вокруг оси . Тогда объем полученного тела вращения вычисляется по формуле

. (9)

Решение. Сделаем чертеж.

Из условия задачи следует, что , . По формуле (9) получаем:

(куб. ед.).

Длина дуги плоской кривой

Пусть кривая , заданная уравнением , где , лежит в плоскости .

Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычис­лить, когда этот...

Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом...

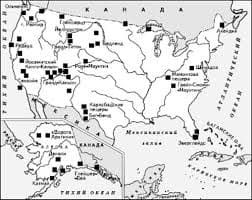Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам...

Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: