Поволжский государственный университет

Поволжский государственный университет

Телекоммуникаций и информатики

Кафедра ТОРС

Конспект лекций по дисциплине

«Основы теории цепей (часть III)»

Составитель: к.т.н., доц. Михайлов В.И.

Самара, 2010 г.

Содержание

Содержание.. 2

1. Теория двухполюсников в ЭЦ.. 3

1.1. Введение в теорию двухполюсников. 3

1.2. Операторное сопротивление двухполюсника и его свойства.. 4

1.3. Реактивные двухполюсники.. 5

1.3.1.Простейшие реактивные двухполюсники. 5

1.3.2. Теорема Фостера о сопротивлении реактивного двухполюсника. 7

1.3.3. Канонические схемы Фостера. 7

1.3.4. Канонические схемы Кауэра. 9

1.3.5. Понятие о синтезе электрических цепей. 11

1.3.6. Виды соответствия двухполюсников. 13

2. Теория четырехполюсников.. 15

2.1. Основные понятия и классификация четырехполюсников. 15

2.2. Основные характеристики четырехполюсников. 16

2.3. Системы параметров. Матричные параметры ЧП.. 16

2.4. Сложные четырехполюсники. Виды соединений ЧП.. 19

2.5. Рабочие параметры ЧП.. 21

2.6. Характеристические параметры четырехполюсника.. 21

2.7. Каскадное согласованное включение четырехполюсников. 23

2.8. Рабочая мера передачи.. 23

Расчет и измерение рабочего ослабления. 24

Связь рабочего и характеристического ослаблений. 25

3. Теория электрических фильтров. 25

3.1. Общие понятия. 25

3.2. Классификация частотно – избирательных электрических фильтров. 26

3.3. Лестничные реактивные фильтры.. 27

3.4. Фильтры типа k.. 29

3.4.1. Основные понятия. 29

3.4.2. Теорема о фильтрах типа k. 30

3.4.3. ФНЧ типа k (полузвено) 30

3.4.4. ФВЧ типа «К» (полузвено) 32

3.4.5. Полосовые фильтры типа «К». 33

3.4.6. Режекторный фильтр типа «К». 34

3.4.7. Достоинства и недостатки фильтров типа k. 35

3.5. Фильтры типа m.. 35

3.5.1. Общие понятия. 35

3.5.2. Последовательно-производный ФНЧ типа m(полузвено) 35

3.5.3. Параллельно-производное полузвено типа m (на примере ФНЧ) 37

3.5.4.ФВЧ типа m.. 39

3.6. Построение сложных фильтров на основе звеньев типа k и m.. 39

3.7. Проектирование фильтров по характеристическим параметрам.. 40

3.8. Проектирование фильтров по рабочим параметрам.. 42

3.8.1. Функция фильтрации. 44

3.8.2. Фильтры Баттерворта. 45

3.8.3. Полиномиальные фильтры Чебышева. 47

3.8.4. Сравнение фильтров Баттерворта и Чебышева. 49

3.8.5. Фильтры со всплесками ослабления (на основе дробей Чебышева и Золотарева) 49

3.9. Методики реализации схем фильтров. 51

3.9.1. Лестничные полиномиальные LC-фильтры.. 51

3.9.2. Реализация фильтров верхних частот, полосовых и заграждающих фильтров. 53

3.9.3. Денормирование по сопротивлению, по частоте при расчете величин элементов. 54

3.9.4. Ускоренный метод синтеза схем фильтра по Попову. 54

Ускоренный метод реализации симметричных фильтров (n-нечетное) 54

Ускоренный метод реализации симметричных фильтров (n-четное) 58

3.10. Расчёт частотных характеристик фильтра.. 61

4. Искажения в ЭЦ при передаче сигналов и их корректирование.. 67

4.1. Искажения сигнала в ЭЦ.. 67

4.2. Корректирующие цепи (корректоры). Общие положения. 67

4.3. Принцип корректирования АЧИ (амплитудно-частотных искажений) 68

4.4. Стандартные схемы амплитудных корректоров. 69

4.5. Фазовые корректоры.. 71

5.Мостовые реактивных фильтры... 74

5.1 Теорема о мостовых реактивных фильтрах.. 74

5.2 Резонаторы и резонаторные фильтры.. 75

Пьезоэлектрические резонаторы и фильтры.. 75

5.3. Модернизированная мостовая схема.. 76

5.4. Широкополосные пьезоэлектрические фильтры.. 77

5.5. Магнитострикционные фильтры.. 80

5.4. Электромеханические фильтры.. 81

6. RC – фильтры... 81

6.1. Общие понятия. 81

6.2. Различные виды RC – фильтров. 81

6.2.1. Фильтры ФНЧ.. 81

6.2.2 Фильтры ФВЧ.. 82

6.2.3 Полосовые фильтры.. 82

6.3. Недостатки RC – фильтров. 83

6.4. Активные RC – фильтры (АRC) 83

6.4.1. Общие понятия. 83

6.4.2. Недостатки АRC – фильтров. Принцип позвенной реализации. 83

6.4.3. АRC – фильтры на усилителях. 84

6.4.4. Фильтры на преобразователях с комплексными коэффициентами. 86

6.4.5. Схема реализации полосового фильтра второго порядка на преобразователях. 87

Теория двухполюсников в ЭЦ

Реактивные двухполюсники

Реактивные двухполюсники содержат только реактивные элементы (L и C). В принципе они неавтономные и могут быть линейными и нелинейными. Эти двухполюсники относят к разряду пассивных, так как они, сколько получают энергии, столько отдают. Соответственно все нули и полюсы располагаются на мнимой оси.

Практически, для реальных цепей реактивные двухполюсники – это двухполюсники из катушек индуктивности и конденсаторов (двухполюсники с малыми потерями).

Канонические схемы Фостера

Канонические схемы – стандартные схемы или схемы, построенные по определенному правилу.

Первая схема Фостера

Первые элементы обозначаются на схеме следующим образом: , далее- четным, а последние . Индексы показывают, на какой частоте происходит полюс у этого элемента или пары элементов.

Для анализа такой схемы удобно воспользоваться операторным сопротивлением:

(здесь четные индексы – полюсы функции сопротивления). Это выражение можно преобразовать в общую дробь:

(в числителе нечетные индексы в знаменателе четные). В знаменателе столько скобок, сколько параллельных контуров в схеме.

Класс реактивного двухполюсника здесь определяет только первая пара элементов (если есть оба элемента, то класс ∞ - ∞; нет ни одного 0 – 0; есть только индуктивность 0 - ∞; есть только емкость ∞ - 0). Пример графика для класса ∞ - ∞;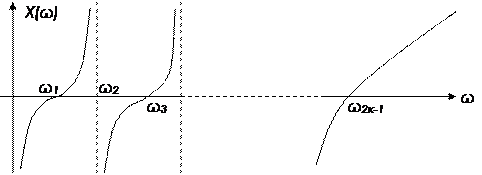

Существует правило для канонических схем: количество элементов в канонической схеме минимальное для получения заданной функции сопротивления (заданного количества резонансных частот, т.е. внутренних нулей и полюсов). Количественно их на единицу больше общего числа резонансных частот (внутренних нулей и полюсов). Также самая старшая степень полинома числителя или знаменателя равна количеству элементов. может равняться при ω→∞ ∞ или 0. При этом емкости заменяются перемычкой, индуктивности заменяются разрывом. Если = ∞, то в первой схеме Фостера и Н малая величина, если =0, то - большая величина. Тогда в первой схеме Фостера; при последовательном соединении с учетом схемы при ω→∞

Вторая схема Фостера

Эта схема дуальна первой схеме Фостера. Первые элементы обозначаются на схеме следующим образом: , далее- нечетным, а последние . Индексы соответствуют полюсам проводимости. Элементы определяют класс двухполюсника (если есть оба элемента, то класс двухполюсника , если нет обоих элементов, то и т.д.). Количество последовательных контуров соответствует количеству резонансных частот напряжения (или скобок в числителе - нулей сопротивления).

Здесь в общем виде удобно записать формулу проводимости:

(здесь индексы нечетные –нули функции сопротивления или полюсы проводимости)

Множитель находится аналогично во второй схеме Фостера. на основе схемы замещения при ω→∞. Если = ∞, то во вторвой схеме Фостера и Н малая величина, если =0, то - большая величина. Тогда во второй схеме Фостера; при последовательном соединении с учетом схемы при ω→∞

Канонические схемы Кауэра

1-ая схема Кауэра

Такая схема называется лестничной или цепной схемой. Сопротивление удобно записать в виде лестничной или цепной дроби:

Класс ДП определяют первый и последний элементы. Если есть оба элемента, то класс ДП

∞-∞; нет ни одного элемента то 0- 0. Количество элементов соответствует старшей степени полинома (на единицу больше числа резонансных частот). В частном случае, если мало элементов, то эта схема может совпадать со схемами Фостера. Множитель также определяется при устремлении ω→∞. Например: Класс ДП 0 – 0 и он содержит 4 элемента (старшая степень равна4 и три резонансных частоты).

X(ω)

0 ω₂ ω₃ ω₄ ω

2- ая схема Кауэра

Первый и последний элементы определяют класс ДП.

Одну и ту же функцию сопротивления реактивного ДП можно получить различными схемами, например, одной из четырех выше описанных. Тогда эти схемы называются эквивалентными (их сопротивление одинаково при любой частоте).

Теория четырехполюсников

Основные понятия и классификация четырехполюсников

Под ЧП понимают ЭЦ, которая соединяется и взаимодействует, т.е. обменивается энергией с другими цепями только через 4 вывода или полюса.

В общем случае выводы четырехполюсника располагаются произвольно:

Частным случаем является проходной () четырехполюсник. У проходного ЧП к одной паре выводов подключается источник сигнала, к другой – нагрузка или потребитель сигнала и поэтому втекающие и вытекающие токи ЧП равны в парных зажимах.

Классификация четырехполюсников очень похожа на классификацию двухполюсников. Четырехполюсники так же делятся на автономные и неавтономные. Автономные четырехполюсники сами создают токи и напряжения без воздействия внешних источников, неавтономные – не создают.

Различают четырехполюсники линейные и нелинейные. Линейные ЧП отличаются от нелинейных тем, что не содержат нелинейных элементов (НЭ) и поэтому характеризуются линейной зависимостью тока и напряжения на выходных зажимах от тока и напряжения на входных зажимах.

Четырехполюсники бывают активными и пассивными. Пассивные схемы не содержат источников электрической энергии, активные - содержат. Последние могут содержать зависимые и независимые источники.

В зависимости от структуры различают ЧП мостовые и лестничные: Г-образные, Т-образные, П-образные. Промежуточное положение занимают Т-образно-мостовые (Т-перекрытые) схемы ЧП.

Четырехполюсники делятся на симметричные и несимметричные. В симметричном ЧП перемена местами входных и выходных зажимов не изменяет напряжений и токов в цепи, с которой он соединен. Четырехполюсники кроме электрической симметрии могут обладать структурной симметрией, определяемой относительно вертикальной оси симметрии. Очевидно, четырехполюсники, симметричные в структурном отношении, обладают электрической симметрией.

Это Т – образный ЧП.

При Z₁ = Z₃ ЧП симметричен

Четырехполюсники могут быть уравновешенными и неуравновешенными. Уравновешенные ЧП имеют горизонтальную ось симметрии и используются, когда необходимо сделать зажимы симметричными относительно некоторой точки (например, земли).

пример уравновешенного ЧП

Четырехполюсники делятся на обратимые и необратимые. Обратимые ЧП позволяют предавать энергию в обоих направлениях одинаково (удовлетворяют теореме обратимости).

Рабочие параметры ЧП

Под рабочими параметрами понимают параметры четырехполюсника, определяемые в рабочем режиме при передаче энергии, т.е. с учетом сопротивлений источника сигнала и нагрузки.

Обычные параметры – внутренние, а рабочие определяются с учетом внешних условий.

Рассматриваются входные/выходные и передаточные параметры.

При расчете входного сопротивления удобно пользоваться матрицей А-параметров:

Если , то входное сопротивление .

Имеем, что в режиме короткого замыкания , а в режиме холостого хода (Z_H=∞) . Так же можно рассматривать и коэффициенты передачи с учетом нагрузочного сопротивления.

Рабочая мера передачи

Рабочая мера передачи оценивает передачу сигнала через ЧП с учетом внутреннего сопротивления источника сигнала и нагрузки в рабочем режиме относительно эталонной цепи передачи сигнала.

Рабочее ослабление – вещественная часть рабочей меры передачи, оценивающая передачу сигнала по изменению полной мощности.

I ₀

Согласуют нагрузку и сопротивление источника Z _2(Н)= Z _1(И).

- оценивает ослабление. Здесь S₀ – полная мощность в эталонной нагрузке, а. S₂ – в рабочей

Рассмотрим важный частный случай, когда сопротивление источника и нагрузки резистивные, т.е. нет реактивных составляющих:

В этом случае источник передает в нагрузку максимально возможную мощность при заданных параметрах.

Получается, что рабочее ослабление оценивает ослабление активной мощности нагрузки, включенной после четырехполюсника, относительно максимума активной мощности, отдаваемой источником в согласованную с ним нагрузку в логарифмических единицах.

Получается, что рабочее ослабление оценивает ослабление активной мощности нагрузки после четырехполюсника относительно наилучшего режима по максимуму мощности.

На практике рабочее ослабление является одним из основных параметров при передаче электрических сигналов, так как сигнал характеризуется принимаемой активной мощностью.

Общие понятия

Под фильтром в общем случае понимают некоторое устройство, работающее по избирательному признаку.

Электрические фильтры (ЭФ) – устройства, которые избирательно, по некоторому правилу пропускают или не пропускают на свой выход электрический сигнал.

Характеристиками электрического сигнала служат частота, напряжение, форма, кодировка и др. Довольно широко распространены ЭФ, где признак избирательности – частота электрического сигнала.

Идеальный частотный фильтр пропускает сигналы с какими – то одними частотами и не пропускает с другими (для одних частот коэффициент передачи 1, для других - 0). В техническом плане основной характеристикой частотных фильтров является рабочее ослабление, поэтому частотный ЭФ – это ЧП, у которого в одной области частот рабочее ослабление мало, близко к 0 (полоса пропускания ПП), а в другой области частот рабочее ослабление велико (полоса задерживания ПЗ(ПН)).

В ПП рабочее ослабление должно быть не больше (меньше) некоторого заданного значения:

В ПЗ рабочее ослабление должно быть не меньше (больше) некоторого заданного значения:

Доказательство

Пусть в нашем случае . Z _1КЗ=jX₁, Z _1XX=jX₁+jX₂

Характеристическое ослабление равно 0, когда

, т.е. числитель и знаменатель – сопряженные. Это возможно, когда число под корнем – отрицательное, т.е. Х₁ и Х₂ разных знаков, и , что соответствует условию теоремы. Таким образом мы доказали условие полосы пропускания.

Если выполняется условие теоремы, то под знаком корня положительное число, т.е. - положительное, резистивное.

Если условие теоремы не выполняется, то под корнем отрицательное число и. - мнимая величина, реактивное сопротивление.

Пример

Условие ПП выполняется там где знаки разные и .

Граничные частоты между полосами пропускания и непропускания называются частотами среза ω_C1 и ω_C2 (f_C1 и f_C2).

Фильтры типа k

Основные понятия

Данные фильтры относятся к лестничным реактивным фильтрам. Состоят из звеньев и полузвеньев.

Основное условие: , где - называют номинальное сопротивление фильтра типа k. ( - взаимообратные двухполюсники).

Теорема о фильтрах типа k

Используя теорему о лестничных реактивных фильтров

в итоге получим условие полосы пропускания (А_С=0).

ФНЧ типа k (полузвено)

Z ₁=jωL Z ₂=1/jωC

 

- номинальное сопротивление полузвена типа к.

Z _КЗ1 =jωL, Z _XX1=j(ωL-1/ωC)

 

 

и , где L и С – параметры полузвена.

0 ωС

 

BC=arg(Г С)

 

+j

RH

0 ωC

-обратное Z _Т

 

 

 

Нагрузку согласуют с сопротивлением фильтра на некоторой частоте согласования (при чем для Т- входа R_H<R₀, а для П- входа R_H>R₀.

При ω=ω_согл,в идеальном случае у фильтров без потерь, А_отр=0, в реальном оно может быть больше 0.

3.4.4. ФВЧ типа «К» ( полузвено)

 

 

 

0 ωC

-j

R0

 

 

0 ωC

+j

R0

3.4.5. Полосовые фильтры типа «К»

 

 

ωС1 ω0 ωС2

ХХХ

 

 

 

 

 

 

 

 

 

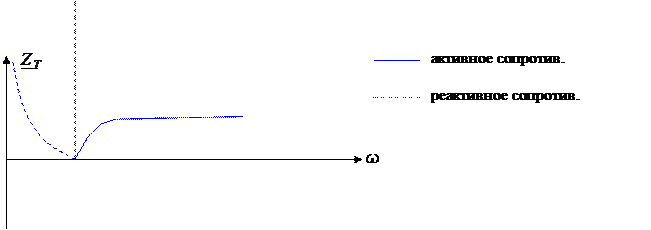
Режекторный фильтр типа «К»

Фильтры типа m

Общие понятия

Эти фильтры получаются из фильтров типа К. Существуют последовательно-производные и параллельно-производные фильтры типа m. Нужно получить звенья фильтров с большей крутизной ослабления и возможностью согласованного включения.

В схеме последовательно-производного фильтра типа m для того, чтобы можно было каскадно согласованно включать фильтры типа k и m.

Получаем, что для равенства , . Характеристическое сопротивление остается таким же, впрочем, как и частота среза. Но характеристика ослабления будет другой с учетом новых резонансных частот.

3.5.2. Последовательно-производный ФНЧ типа m (полузвено)

Применим теорему о лестничных фильтрах. Изобразим графики.

ω_C ▪ mL= , отсюда , а R ₀= .

Используют и нормированную частоту Ω= ω/ ω_C При Х₂ (ω_∞)= 0 (резонанс напряжений в последовательном контуре) А_С=∞.

Здесь график может быть с минимумом при . Вообще 0< .

Для определения ω_∞ запишем уравнение Х₂ =0

Если , то получаем фильтр типа k (ω_∞=∞)

.

Можем сделать вывод, что чем меньше m, тем ближе к. ω_С и тем круче характеристика ослабления. Чем больше m, тем больше .и менее крутая характеристика А_С.

Достоинства:

На графике получается минимум, когда . В этом случае получаем хорошее согласование (две частоты согласования) При этом R _Н < R ₀.

Крутизна нарастания рабочего ослабления больше.

Недостатки:

· после рабочее ослабление уменьшается;

· более сложная схема, следовательно, больше элементов и расчетные формулы сложнее.

3.5.3. Параллельно-производное полузвено типа m (на примере ФНЧ)

L₁= m L C₁= C₂= m C

 

ω_с= ω_∞ =

R ₀=

0 ωС

0 ωC ω∞

 

0 ωС

 

 

со стороны Т- входа

ωC

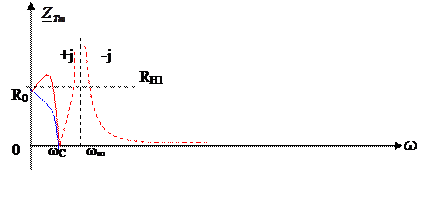
Здесь график Z_Т может быть с максимумом при .

 

ФВЧ типа m

Х₁= , Х₂= Х₁= Х₂=ωL₂

последовательно- производное полузвено параллельно-производное полузвено

Все характеристики ФВЧ повернуты на 180⁰ относительно характеристик ФНЧ, т.е. сначала идет полоса непропускания, затем – пропускания.

Функция фильтрации

В теории электрических фильтров фильтры описываются передаточной функцией вида:

(1)

При этом рабочее ослабление при использовании нормированной частоты

(2)

Здесь – нормированная частота, а - нормирующая частота. Обычно в качестве нормирующей выбирают граничную частоту полосы пропускания ω₂.

Функция называется функцией фильтрации, а - коэффициентом неравномерности ослабления. В общем случае - дробно-рациональная функция с вещественными коэффициентами (в частности полином), удовлетворяющая условиям: в полосе пропускания и в полосе непропускания фильтра.

В зависимости от вида функции фильтрации получают различные типы фильтров. Если в качестве функции фильтрации используют полиномы, то фильтры называются полиномиальными. Среди полиномиальных фильтров широкое использование нашли фильтры Баттерворта и Чебышева. Если - дробно-рациональная функция, например, дробь Золотарева, то получают фильтр Золотарева - Кауэра.

Следует отметить, что есть смысл подробно изучать только ФНЧ, т.к. другие типы фильтров могут быть легко получены из ФНЧ заменой (преобразованием) частоты.

Фильтры Баттерворта

Если в выражениях, описывающих квадрат АЧХ фильтра (1) и его рабочее ослабление (2), в качестве функции фильтрации используются полиномы Баттерворта , то такие фильтры называются фильтрами Баттерворта.

Из формул (1) и (2) следует, что для фильтров Баттерворта на частоте значение квадрата АЧХ равно единице, а рабочего ослабления – нулю. С ростом частоты квадрат АЧХ фильтра Баттерворта уменьшается и падает до нуля на бесконечно большой частоте. Рабочее ослабление плавно растет до бесконечно большого значения. Таким образом, выражения (1) и (2) приближенно воспроизводят характеристики идеального фильтра.

Чтобы эти характеристики «вписывались» в предъявляемые к фильтру требования, необходимо иметь рабочее ослабление (2) в полосе пропускания меньше ΔА= , а в полосе непропускания большее . Первому условию можно удовлетворить, если потребовать на граничной частоте полосы пропускания () выполнения равенства или . Отсюда с учетом (1) И (2) имеем , вычисляем коэффициент: (3),

который называется коэффициентом неравномерности ослабления в полосе пропускания фильтра. В этой формуле величина имеет размерность непер. Если воспользоваться значениями в дБ, то (4). 0 < ε Если ε=1, то А_Р=3 дБ.

С учетом введенных обозначений квадрат АЧХ фильтра Баттерворта запишется в виде:

Эта функция удовлетворяет свойствам квадрата АЧХ реальных ЧП, и поэтому ей можно сопоставить физически осуществимый фильтр.

Рабочее ослабление фильтра Баттерворта:

, дБ

, Нп Крутизна частотных характеристик зависит от степени n – порядка фильтра. Чем больше степень n, тем выше крутизна характеристики.

Таким образом, для удовлетворения требований в полосе непропускания необходимо выбрать соответствующий порядок фильтра n. Его легко определить из условия: на граничной частоте полосы непропускания Ω₃:

или . С учетом этого условия получаем: , откуда . Логарифмируя обе части неравенства, придем к окончательному выражению:

. Здесь Ω₃=ω₃/ω₂ Округление производится в большую сторону до целого числа.

Величина входит в формулу в неперах. Если вычислять ее в децибелах, то

.Фильтры Баттерворта называют также фильтрами с максимально плоским ослаблением в полосе пропускания.

где

Корни уравнения , лежащие в левой полуплоскости, принадлежат , являющемуся полиномом Гурвица. Следовательно, функция: удовлетворяет условиям физической реализуемости.

Эти корни определяются соотношениями:

и позволяют найти искомую передаточную функцию в виде:

. (3.7)

Рабочее ослабление нетрудно теперь получить через передаточную функцию на основании:

дБ.

Пример расчета

Ниже приведен пример расчета характеристик ФНЧ Чебышева 4 порядка с DA=0,2 дБ, f₂=1000Гц, f₃=2400Гц, A_min = 30 дБ с использованием MathCAD 2000 русская версия. Причем для ускорения расчетов определитель сразу записан в операторном виде. Так же представлена схема фильтра.

R1=291, R2=450, L1=0.0605, C2=7,002*10^-7, L3=0,0918, C4=4,612*10⁼⁷,

Графики зависимости рабочего ослабления для полос непропускания и пропускания приведены на рисунке.

ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала...

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право...

Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все...

Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: