|
|
Теорема Фостера о сопротивлении реактивного двухполюсникаКомплексное сопротивление реактивного двухполюсника можно представить функцией, выраженной через ее нули и полюса (резонансные частоты):
где Н – некоторый множитель, положительное вещественное число; ω – угловая частота; ωк – резонансные частоты (математически нули и полюсы). Принято в числителе использовать нечетные индексы (нули функции сопротивления ДП) в знаменателе четные (полюсы функции сопротивления ДП). Из этой формулы можно получить частные случаи, соответствующие классам двухполюсников. Для классов 0 - ∞, 0 – 0 ω1=0. Для классов ∞ - 0, ∞ - ∞
Производная по частоте всегда положительная: Нули и полюсы всегда чередуются. Старшая и младшая степени полиномов числителя и знаменателя отличаются не более, чем на единицу (нули и полюсы в начале и конце координат – простые). Дробь (1) представляет собой либо отношение нечетного полинома к четному, либо четного к нечетному. Множитель Н по своему смыслу соответствует эквивалентной индуктивности или величине, обратной эквивалентной емкости при Канонические схемы Фостера Канонические схемы – стандартные схемы или схемы, построенные по определенному правилу. Первая схема Фостера
Первые элементы обозначаются на схеме следующим образом: Для анализа такой схемы удобно воспользоваться операторным сопротивлением:
Класс реактивного двухполюсника здесь определяет только первая пара элементов (если есть оба элемента, то класс ∞ - ∞; нет ни одного 0 – 0; есть только индуктивность 0 - ∞; есть только емкость ∞ - 0). Пример графика для класса ∞ - ∞;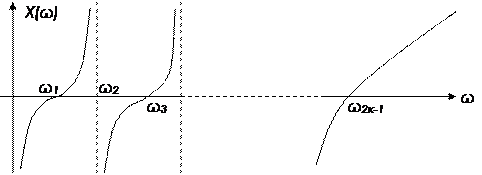 
Существует правило для канонических схем: количество элементов в канонической схеме минимальное для получения заданной функции сопротивления (заданного количества резонансных частот, т.е. внутренних нулей и полюсов). Количественно их на единицу больше общего числа резонансных частот (внутренних нулей и полюсов). Также самая старшая степень полинома числителя или знаменателя равна количеству элементов. Вторая схема Фостера Эта схема дуальна первой схеме Фостера. Первые элементы обозначаются на схеме следующим образом:
Здесь в общем виде удобно записать формулу проводимости:
Множитель Канонические схемы Кауэра 1-ая схема Кауэра
Такая схема называется лестничной или цепной схемой. Сопротивление удобно записать в виде лестничной или цепной дроби:
Класс ДП определяют первый и последний элементы. Если есть оба элемента, то класс ДП
X(ω)
0 ω2 ω3 ω4 ω
2- ая схема Кауэра
Первый и последний элементы определяют класс ДП.
Одну и ту же функцию сопротивления реактивного ДП можно получить различными схемами, например, одной из четырех выше описанных. Тогда эти схемы называются эквивалентными (их сопротивление одинаково при любой частоте).   Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам...  Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...  Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все...  Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|
(1),
.
.
, далее- четным, а последние 
. Индексы показывают, на какой частоте происходит полюс у этого элемента или пары элементов.
(здесь четные индексы – полюсы функции сопротивления). Это выражение можно преобразовать в общую дробь:
(в числителе нечетные индексы в знаменателе четные). В знаменателе столько скобок, сколько параллельных контуров в схеме.
может равняться при ω→∞ ∞ или 0. При этом емкости заменяются перемычкой, индуктивности заменяются разрывом. Если 
= ∞, то в первой схеме Фостера 
и Н малая величина, если 
=0, то 
- большая величина. Тогда в первой схеме Фостера; при последовательном соединении с учетом схемы при ω→∞ 
, далее- нечетным, а последние 
. Индексы соответствуют полюсам проводимости. Элементы 
, если нет обоих элементов, то 
и т.д.). Количество последовательных контуров соответствует количеству резонансных частот напряжения (или скобок в числителе - нулей сопротивления).
(здесь индексы нечетные –нули функции сопротивления или полюсы проводимости)
находится аналогично во второй схеме Фостера. на основе схемы замещения при ω→∞. Если 
= ∞, то во вторвой схеме Фостера 
и Н малая величина, если 
∞-∞; нет ни одного элемента то 0- 0. Количество элементов соответствует старшей степени полинома (на единицу больше числа резонансных частот). В частном случае, если мало элементов, то эта схема может совпадать со схемами Фостера. Множитель 
