|
|
Фильтры на преобразователях с комплексными коэффициентами⇐ ПредыдущаяСтр 12 из 12
Модель реализации звеньев на преобразователях была разработана Михайловым В.И. Один из вариантов содержит ПТН и ПНТ, работающие в разных направлениях.
. ПТН - преобразователь тока в напряжение, ПНТ – напряжения в ток. В матрице передачи А преобразователя только один ненулевой параметр Реализация этих преобразователей возможна на микросхемах и ОУ. Матрица идеального ПТН
Схема реализации ПТН Схема замещения ПТН:
Матрица идеального ПНН
Z BX= Z 1, Z ВЫХ=0 (не совсем идеальный). Если к данной схеме добавить
Схема реализации полосового фильтра второго порядка на преобразователях
Здесь использованы ПТН в прямом направлении и ПНТ в обратном.
Данная схема звена ПФ была разработана Михайловым В.И. и так же была использована для реализации эквивалента мостовой схемы с резонаторами и параллельными расширительными индуктивностями. Резонатор включался параллельно емкости С1.
Здесь в 1 секции ПТН1 (ИНУТ) имеет параметр преобразования
Схема и ослабление активного пьезоэлектрического широко полосного полосово 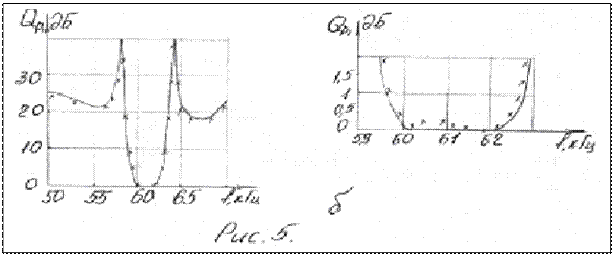 го фильтра го фильтра
Проводимость резонатора по классу будет 0-∞ с 2 резонансами.Если параллельно включить индуктивность, то получим общую проводимость как сумму проводимостей и класс ∞-∞ с 3 резонансными частотами. Резонансный промежуток при этом увеличивается с 0,4% от средней частоты до 4%.
Дискретные сигналы. Модель дискретного сигнала. Дискретные цепи
Электрические цепи работающие с дискретными сигналами называют дискретными Сигналы как процессы, передающие информацию о состоянии физических систем, описываются математическими моделями в виде функций времени. Непрерывные (аналоговые) сигналы определены на непрерывном временном множестве и характеризуются непрерывном множеством принимаемых значений. Дискретные сигналы определены на дискретном временном множестве. Цифровые сигналы определены на дискретном временном множестве и характеризуются дискретным множеством принимаемых значений.
Математическая модель аналогового сигнала: Математическая модель дискретного сигнала: Отсчеты дискретного сигнала производятся через постоянный промежуток времени:
Для удобства анализа дискретных систем используют модель дискретного сигнала в виде:
МИП можно представить также в виде: С физической точки зрения МИП описывает сигнал на выходе устройства, в котором реализуется операция умножение входного аналогового сигнала
Импульсный сигнал (дискретизирующая последовательность) D(t) – периодическая функция с периодом
Синтез ARC-фильтров. Синтез активных RC -фильтров, так же как и LC -фильтров состоит из двух этапов: аппроксимации и реализации. На этапе аппроксимации получают аналитическое выражение рабочей передаточной функции T(p) фильтра, удовлетворяющей заданным техническим условиям (методика аппроксимации ARC -фильтров такая же, как и LC -фильтров). На этапе реализации по найденной рабочей передаточной функции определяется схема фильтра и величины ее элементов. Реализация ARC –фильтров существенно отличается от реализации LC -фильтров и даёт значительно большую неоднозначность схемных решений. В данной методической разработке рассматривается один из многочисленных способов (методов) реализации ARC -фильтров. Использование нормирования и преобразования частоты позволяет расчёт всех типов фильтров (ФНЧ, ФВЧ, ПФ, ЗФ и т.д.) свести к расчёту фильтра нижних частот, который принято называть прототипом (ФНЧП). Расчёт удобно проводить в следующем порядке: 1. От технических требований заданного типа переходят к техническим требованиям ФНЧП. 2. Производят аппроксимацию характеристики рабочего ослабления и получают аналитическое выражение нормированной рабочей передаточной функции T(p) ФНЧП. 3. С помощью соответствующего преобразования частоты получают нормированную передаточную функцию T(p) фильтра заданного типа. 4. Производят денормирование рабочей передаточной функции. 5. Полученную рабочую передаточную функцию представляют в виде произведения сомножителей 1-го или 2-го порядка (в зависимости от выбранного активного элемента, добротности, чувствительности и т.д.). Для каждого звена по его схеме известными в ТЭЦ методами определяется его передаточная функция, выраженная через параметры входящих в схему элементов, что в дальнейшем позволяет с помощью системы компонентных уравнений рассчитать величины элементов каждого звена. Составляют полную схему фильтра в виде каскадного соединения отдельных звеньев, располагая звенья в порядке увеличения добротности. 6. Рассчитывают рабочее ослабление полученного фильтра на характерных частотах ПП и ПЗ и убеждаются в соответствии с заданными техническими требованиями. Переход к ФНЧП.   Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...  Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом...  Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот...  ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|