|
|
Продолжим исследование логарифмической функции.1) D(f-1)=E(f)=(0;+∞); прямая х=0-вертикальная асимптота 2) E(f-1)=D(f)=R 3)Имеем корень х=1, т.к. а0=1 4) Функция строго монотонна и непрерывна (при а>1 возрастает; при 0 < а < 1 убывает) Функция общего вида. Экстремумов нет График логарифмической функции симметричен графику показательной функции относительно прямой у=х.
Пример 1. С помощью преобразований графиков построить график данной функции и провести исследование. у=| Решение: Порядок работы: (1) у= (4) у=| Схема графика имеет вид:
Исследование: 1) D(f)=R 2) E(f)=[0;+∞) 3) y=0« 4) f(-x)=f(x) ®чётная функция. 5) min y(±3)=0; max y(0)=2. Пример 2. С помощью преобразований графиков построить график данной функции и провести исследование. y=| Решение: Порядок работы: (1) у= (4) y=| Схема графика имеет вид:
Исследование: 1) D(f)=(-∞;-1)∪(-1;+∞); прямая х=-1- вертикальная асимптота. 2) E(f)=[0;+∞) 3) y=0« 4) Функция общего вида (график симметричен относительно прямой х=-1) 5) min y(-5)=0; min y(3)=0. (Обратите внимание на различие графиков функций в 1-ом и 2-ом примерах, несмотря на похожесть формул задания) Пример 3 С помощью преобразований графиков построить график данной функции и провести исследование. у=| Решение: Порядок работы: (1) у= (4)у =| Схема графика имеет вид:
Исследование: 1) D(f)=(-∞;-2)∪(2;+∞); прямые х=-2 и х=2- вертикальные асимптоты. 2) E(f)=[0;+∞). 3) y=0« 4) f(-x)=f(x)-чётная функция. 5) min y(±4)=0. Пример 4 С помощью преобразований графиков построить график данной функции и провести исследование. у=| Решение: Порядок работы: (1) у= (4) у=| Схема графика имеет вид:
Исследование: 1) D(f)=(-∞;2)∪(2;+∞); прямая х=2- вертикальная асимптота. 2) E(f)=[0;+∞) 3) у=0« 4) Функция общего вида (прямая х=2- ось симметрии). 5) min y(0)=0; max y(4)=0. Пример 5(самостоятельно). С помощью преобразований графиков построить график данной функции и провести исследование. у=| Пример 6 (самостоятельно) С помощью преобразований графиков построить график данной функции и провести исследование. у=| Пример 7 (самостоятельно). С помощью преобразований графиков построить график данной функции и провести исследование. у=| Пример 8 (самостоятельно) С помощью преобразований графиков построить график данной функции и провести исследование. у=| Пример 9. Дано: f(x)= Найти: E(f);2) определить вид отображения f (построить график). Решение: Функция у= Данная функция получена из исходной параллельным переносом, а следовательно тоже убывает Вывод: f- биекция. Вычислим значение функции на границах области определения: f(5)=2; f(7)=1® E(f)=[1;2].
Пример 10. Дано: f(x)= Найти: E(f);2) определить вид отображения f (построить график). Решение: Заметим, что данная функция чётная. Область определения: 4-|х|>0«хÎ(-4;4) (прямые х=±4-вертикальные асимптоты) В нашем примере D(f)=[-1;3]Ì(-4;4) Вычислим значение функции на границах интервала и в точке х=0. f(-1)=0; f(3)=1; f(0)= Схема графика:
На интервале [-1;0] функция убывает, а на интервале [0;3]возрастает®нет строгой монотонности. Т.к. по условию E(f)=Y, то данное отображение является сюръекцией (отображение Х на У) E(f)=[ Пример 11(самостоятельно). Дано: f(x)= Найти: E(f);2) определить вид отображения f (построить график). Ответ:E(f)=[-4;-1]; биекция. Пример 12(самостоятельно). Дано: f(x)= Найти: E(f);2) определить вид отображения f (построить график). Ответ: E(f)=[ Пример 13. Решить уравнение: | Решение: Пусть t= Покажем графическое решение данного уравнения.
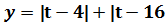 |; t>0 «корыто» |; t>0 «корыто»
4≤t≤16«4 ≤ Ответ:хÎ[3;15] Пример 14. Решить уравнение: | Решение: Пусть Покажем графическое решение данного уравнения.
 | («ступенька») у(1)=1; у(2)=-1. | («ступенька») у(1)=1; у(2)=-1.
t≤1« Ответ: хÎ(-1;1] Пример 15(самостоятельно). Решить уравнение: | Ответ: xÎ[3;6]. Пример 16(cамостоятельно). Решить уравнение: | Ответ: хÎ(-∞;1,5] Пример 17. Решить неравенство.
Решение:
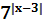 ; (2)g(x)= ; (2)g(x)= 
(1)
 min f(3)=1®f(x)³1 min f(3)=1®f(x)³1
(2)
0<t(x)≤2«-∞< По условию:f(x)≤g(x) при этом Ответ:{3}. Пример 18. Решить неравенство.
Решение: Рассмотрим две функции: (1) f(x)= Решаем неравенство: f(x)³g(x). (1)f(x)=
(2) g(x)=
Ответ:{0}. Пример 19(самостоятельно). Решить неравенство.
Ответ:{4}. Пример 20(самостоятельно). Решить неравенство.
Ответ:{-1}. Пример 21. Решить уравнение.
Решение: Имеем верное равенство при всех допустимых значениях аргумента:
 « « 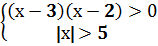
Ответ: ХÎ(-∞;-5)∪(5;+∞) Пример 22(cамостоятельно). Решить уравнение:
Ответ: хÎ(3;4). Сложная функция.   Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...  Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем...  ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования...  Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|