|
|
Данная функция строго монотонна, а именно убывает.Сделаем контрольную проверку. Пусть х1=2® f(2)=-1; x2=1®f(1)=6. x1>x2®f(x1)<f(x2)®функция убывает. Следовательно, существует обратная функция, при этом E(f-1)=D(f)=(-∞; Ответ: (-∞; Пример 13 (самостоятельно). Найти E(f-1)по заданной функции у=f(x), если у= Ответ: (-∞;- Пример 14 (самостоятельно). Найти E(f-1)по заданной функции у=f(x), если у= Ответ: (-∞; Пример 15. Найти E(f-1)по заданной функции у=f(x), если у= Ответ: (-∞;5,5]. Пример 16 (самостоятельно). Найти E(f-1)по заданной функции у=f(x), если у= Ответ: (-∞;+∞). Пример 17. Дано: у= Найти: 1)обратную функцию;2) построить графики функций f(x)и f-1(x). Решение: 1.Построим график функции у=
2.D(f)=(-∞;+∞) 3.E(f)=(-2;+∞); у=-2-горизонтальная асимптота. Функция непрерывная и строго возрастает Существует обратная функция. Находим формулу обратной функции, выражая переменную х через у. у= 6.Для построения графика обратной функции в старой системе координат поменяем местами переменные:х«у: у= 7.D(f-1)=E(f)=(-2;+∞); х=-2-вертикальная асимптота. 8.E(f-1)=D(f)=(-∞;+∞). 9.f-1 возрастает и непрерывна. Напомним, что графики взаимно обратных функций симметричны относительно прямой у=х. Пример 18. Дано: y= Найти: 1)обратную функцию;2) построить графики функций f(x)и f-1(x). Решение:
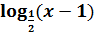 +2 +2
2.D(f)=(1;+∞); x=1-вертикальная асимптота. 3.E(f)=(-∞;+∞). Функция непрерывна и строго убывает. Существует обратная функция. Находим формулу обратной функции, выражая переменную х через у. y= Для построения графика обратной функции в старой системе координат поменяем местами переменные:х«у =( 7.D(f-1)=E(f)=(-∞;+∞). 8.E(f-1)=D(f)=(1;+∞); y=1-горизонтальная асимптота. Функция непрерывна и убывает. Пример 19. Дано: у=х2-7х+12. Определить интервалы монотонности и на каждом интервале найти обратную функцию. Построить графики. Решение: у=х2-7х+12«у=(х-3,5)2-0,25-это парабола. ü х=3,5- ось симметрии ü (3,5;-0,25)-вершина параболы ü корни: х1=3; х2=4. ü у(0)=12.
Имеем два интервала монотонности.
Замечание: Обратите внимание, что f1=f2= х2-7х+12. Но обратные функции имеют различные формулы задания. Но, если построить графики обратных функций в одной системе координат, то получим тоже параболу, которую задают уравнением: (у-3,5)2=х+0,25.
Пример 19. Дано: у= Определить интервалы монотонности и на каждом интервале найти обратную функцию. Построить графики. Решение: Данная функция задаётся объединением двух формул, если раскрыть знак модуля. у= Схема графика:
Имеем два интервала монотонности.
Пример 20.
Имеем ломаную и три интервала монотонности.
D(f1)=[-3;0]; проходит через точку (-3;0) с угловым коэффициентом к1=1/3 Уравнение прямой ищем в виде: у=к1(х-х0)+у0®у=1/3(х+3).
коэффициентом к2=-1
D(f3)=[2;5]; проходит через две точки М1(2;-1) и М2(5;4). Уравнение прямой ищем в виде: 5(х-2)=3(у+1)«у= Окончательно получаем объединённую формулу задания данной функции. f(x)= Далее на каждом интервале монотонности определим обратную функцию и проведём полное исследование. Обратите внимание, что нельзя найти единой обратной функции, но можно определить обратную функцию на выбранном участке монотонности.
Пример 21. Дано: у=|х-1|+2|х+3|-2х+1. Построить график данной функции и определить интервалы монотонности.   Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...  Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? - задался я вопросом...  ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала...  Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|