|
|
На каждом интервале монотонности найти обратную функцию.Решение: Раскроем знак модуля и получим задание данной функции как объединение формул: у= у= Строим график данной функции и определяем интервалы монотонности.
Пример22 (творческое задание) Задайте график ломаной. Найдите аналитическое задание этой функции. На каждом интервале монотонности найдите обратную функцию и проведите полное исследование. Пример 23 (творческое задание) Дано: у=к1|х-а|+к2|х-b|+k3x+c 1) Задайте параметры (к1;к2;к3;a;b) Постройте график данной функции. На каждом интервале монотонности найдите обратную функцию. Примечание: Обратите внимание на задание функции: Не должно быть участков, где функция постоянная. В противном случае Вы не сможете найти обратную функцию. Желаю успеха! Глава 8. Тригонометрические и обратные тригонометрические функции и их свойства. Периодические функции и их свойства. Определение: Функция у=f(x), заданная на множестве X, называется периодической, если существует такое число L (L 1) ∀xÎX, x±LÎX; 2)∀xÎX; f(x±L)=f(x).
Число L называется периодом данной функции, а сама функция периодической. Основные свойства периодических функций 1. Если L -период функции y=f(x), то функция имеет бесконечное множество периодов вида {kL}, k Другими словами, если L-период функции y=f(x), то числа: ±2L;±3L;…тоже периоды данной функции. Действительно, пусть L -период функции y=f(x). Покажем, что число 2L - тоже период этой функции. ∀xÎX, x±LÎX®x±2LÎX f(x+2 L)=f((x+ L)+L)=f(x+L)=f(x) f(x+2 L)=f(x)
Определение: Наименьшее положительное число из множества всех периодов называется основным периодом, который мы будем обозначать Т. Напомним основные периоды для тригонометрических функций: 1) y=sin x, T=2π (sin(x±2π)=sin x) 2) y=cosx, T=2π (cos(x 3) y=tgx, T=π (tg(x 4) y=ctgx, T=π (ctg(x
При построении графика периодической функции можно сначала построить график на интервале длины T, а затем периодически продолжить график на всю числовую ось. Замечание: Если y=f(x) – чётная, то строим график на интервале [0; Затем чётным образом на интервале [- Аналогично для нечётной функции, только на интервале [- 3. Если функция y=f(x) имеет период Т, то функция y=Аf(kx+b)+ B имеет период (А, В, k, b) – постоянные) 4. Если функция f1(x) имеет период Т1, функция f2(x) имеет период Т2, то функция y=Аf1(x)+ B f2(x) тоже периодическая с периодом T. Для нахождения T используем соотношение: kТ1=nТ2 (k,n
Тогда, Т= Определение тригонометрических функций. Рассмотрим окружность, заданную уравнением: х2+у2=1; R=1. (В дальнейшем будем называть эту окружность тригонометрической). Пусть радиус-вектор Пусть координаты точки М(х.; у).
Определение: R=1®
Ось (оу) называют осью синусов.
R=1®
Ось (ох) называют осью косинусов. Таким образом, точка М на тригонометрической окружности имеет координаты М( Замечание: Аргументом синуса и косинуса является угол поворота 𝛂. Если этот угол выражается в радианах, то значениями 𝛂 являются действительные числа. Напомним, что радиан (от лат radius) можно определить как центральный угол, который опирается на дугу, равную радиусу.

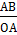 =tg𝛂, т.к. ОА=1® =tg𝛂, т.к. ОА=1®
tgα=AB. Прямая х=1 называется осью тангенсов.
Рассмотрим прямую у=1.
В-точка пересечения Тогда Прямая у=1 называется осью котангенсов. §3. Функция у= Исследование: 1. D(f)=(-∞;+∞). 2. E(f)=[-1;1]. 3. 4. 5. Основной период Т=2π; Т.к. функция нечётная и периодическая, то достаточно исследовать функцию на интервале [0;π]. 6.Если х возрастает от 0 доπ/2, то функция возрастает от 0 до 1. Если х возрастает от π/2 до π, то функция убывает от 1до 0. 7.min y=-1; max y=1;   Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все...  ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между...  Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)...  ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры... Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
|